AI Studio 不同环境下的执行速度
Posted 卓晴
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了AI Studio 不同环境下的执行速度相关的知识,希望对你有一定的参考价值。

简 介: 对比了AI Studio中的三种运行环境。基础版本、高级版本以及至尊版本。它们的配置是越来越高的。通过两种方式进行测试: 测试对于大型矩阵求逆; 测试resnet50识别动物;可以看到实际上基础版本程序中,对于矩阵求逆运行速度是最快的。在图像识别中,智尊版本运行时间最快,但三个版本的差别并不是很大。那么问题来了,这三个环境的配置,难道仅仅说说玩玩的吗?毕竟对于基础版本在使用费用上是没有限制的,而其他两个版本则是要求需要计算卡的呀?
关键词: AI Studio,速度测试
§01 切换环境
一、三种不同执行环境
在AI Studio中,进入Notebook Project之后,有三种执行环境。它们的配置以及所需要的费用如下:
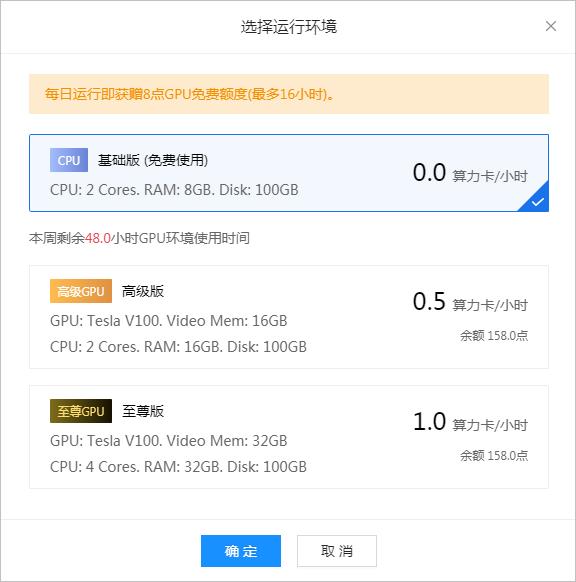
▲ 图1.1.1 三种运行环境
1. 基础版环境内仅有CPU计算资源,可切换到不同的GPU计算资源.
2. 切换环境耗时较久, 因此仅当项目文件小于1GB时才能执行.
3. 如需切换至基础版环境, 请注意修改代码中GPU设置部分.
如需切换至GPU版环境, 还需要满足:
a. 算力卡余额>0.
b. 没有其他项目正在使用GPU版环境.
通过上面说明,我们自然而然的认为,一个程序在基础版环境下的运行速度应该比在高级版、至尊版运行环境下的速度要慢。是不是这样,下面通过实际测试来看一下这三种运行环境下程序速度。
二、 不同环境速度测试
1、矩阵求逆
(1)测试代码
from headm import *
MATRIX_DIM = 100
a = random.randn(MATRIX_DIM, MATRIX_DIM)
printf(a.shape)
starttime = time.time()
ainv = linalg.inv(a)
rst = a.dot(ainv)
ellapsetime = time.time() - starttime
print("Cost time:s".format(ellapsetime))
plt.imshow(rst)
plt.show()
(2)测试结果
Ⅰ.在Notebook中测试
| MATRIX DIM | Cost Time |
|---|---|
| 100 | 0.5289s |
| 200 | 5.2696s |
| 300 | 13.5553s |
| 400 | 34.4000s |
| 500 | 32.6816s |
| 600 | 44.8908s |
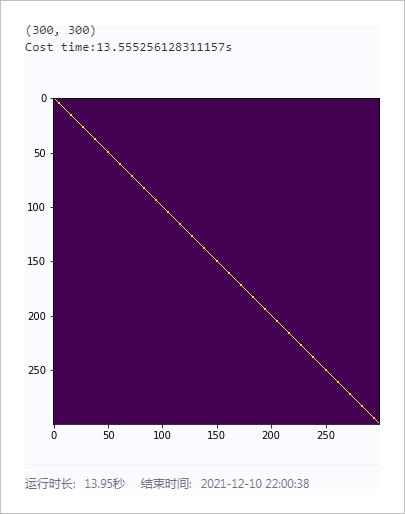
▲ 图1.2.1 矩阵求逆以及恢复原有的结果
Ⅱ.连续测试
from headm import *
dim = (100, 200, 300, 400, 500, 600, 700, 800)
timedim = []
for d in dim:
MATRIX_DIM = d
a = random.randn(MATRIX_DIM, MATRIX_DIM)
printf(a.shape)
starttime = time.time()
ainv = linalg.inv(a)
rst = a.dot(ainv)
ellapsetime = time.time() - starttime
timedim.append(ellapsetime)
print("Cost time:s".format(ellapsetime))
plt.plot(dim, timedim)
plt.xlabel("Dimenstion")
plt.ylabel("Ellapse Time")
plt.grid(True)
plt.tight_layout()
plt.show()
(100, 100)
Cost time:0.577387809753418s
(200, 200)
Cost time:5.287629127502441s
(300, 300)
Cost time:13.601109027862549s
(400, 400)
Cost time:21.799143314361572s
(500, 500)
Cost time:31.697691917419434s
(600, 600)
Cost time:46.29343271255493s
(700, 700)
Cost time:59.27834343910217s
(800, 800)
Cost time:72.15428853034973s
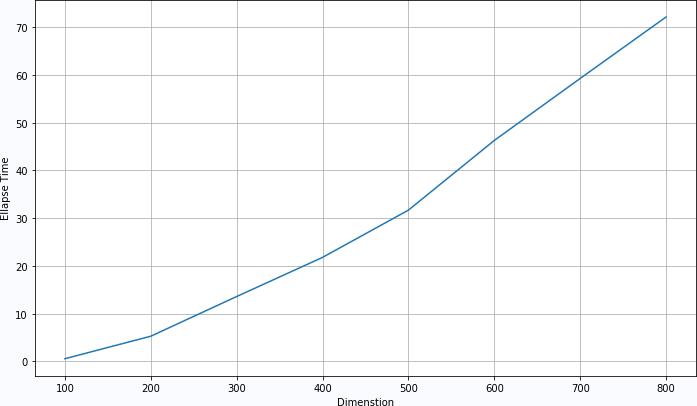
▲ 图1.2.2 不同的矩阵尺寸对应的执行时间
Ⅲ.在Terminal测试
(100, 100)
Cost time:0.5420284271240234s
(200, 200)
Cost time:4.893026113510132s
(300, 300)
Cost time:14.19676685333252s
(400, 400)
Cost time:21.32607650756836s
(500, 500)
Cost time:31.28787326812744s
(600, 600)
Cost time:44.49827766418457s
(700, 700)
Cost time:65.78703761100769s
(800, 800)
Cost time:72.45447182655334s
Ⅳ.两个环境差异
Dim 100 200 300 400 500 600 700 800
T1 0.58 5.29 13.60 21.80 31.70 46.29 59.28 72.15
T2 0.54 4.89 14.20 21.33 31.29 44.50 65.79 72.45
Err 0.04 0.39 -0.60 0.47 0.41 1.80 -6.51 -0.30
| Dim | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 |
|---|---|---|---|---|---|---|---|---|
| T1 | 0.58 | 5.29 | 13.60 | 21.80 | 31.70 | 46.29 | 59.28 | 72.15 |
| T2 | 0.54 | 4.89 | 14.20 | 21.33 | 31.29 | 44.50 | 65.79 | 72.45 |
| Err | 0.04 | 0.39 | -0.60 | 0.47 | 0.41 | 1.80 | -6.51 | -0.30 |
from headm import *
id1 = 12
id2 = 15
strall = tspgetdopstring(id1).split('\\r\\n')
item1 = list(zip(*([iter(strall)]*2)))
strall = tspgetdopstring(id2).split('\\r\\n')
item2 = list(zip(*([iter(strall)]*2)))
def dimsecond(dd):
timedim = []
for d in dd:
dimension = int(d[0][1:4])
id = d[1].find(':')
time = float(d[1][id+1:-1])
timedim.append((dimension, time))
return timedim
td1 = dimsecond(item1)
td2 = dimsecond(item2)
dimdim = [d[0] for d in td1]
timedim1 = [d[1] for d in td1]
timedim2 = [d[1] for d in td2]
errdim = [e1-e2 for e1,e2 in zip(timedim1,timedim2)]
printf('Dim ' + ' '.join([str(t) for t in dimdim]))
printf('T1 ' + ' '.join(['%3.2f'%t for t in timedim1]))
printf('T2 ' + ' '.join(['%3.2f'%t for t in timedim2]))
printf('Err ' + ' '.join(['%3.2f'%t for t in errdim]))
(3)高级版本工作环境
(100, 100)
Cost time:3.9402291774749756s
(200, 200)
Cost time:28.295919179916382s
(300, 300)
Cost time:71.13294100761414s
(400, 400)
Cost time:111.89861345291138s
(500, 500)
Cost time:173.6553499698639s
(600, 600)
Cost time:191.19679641723633s
(700, 700)
Cost time:228.57337856292725s
(800, 800)
Cost time:268.878142118454s
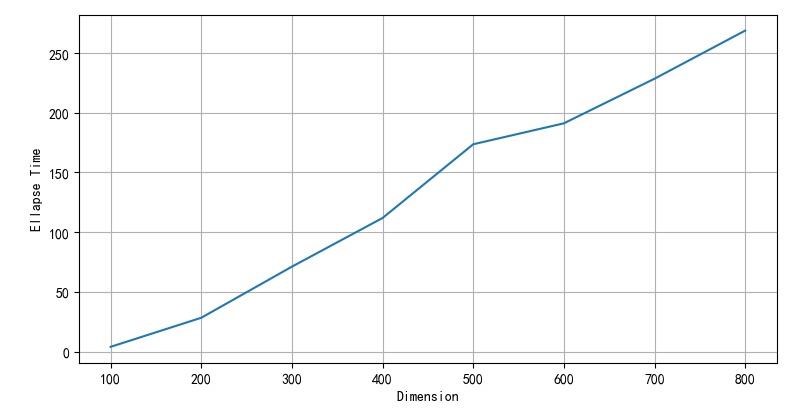
▲ 图1.2.3 数组长度与求逆时间
(4)至尊版工作环境
(100, 100)
Cost time:1.0169579982757568s
(200, 200)
Cost time:9.981705665588379s
(300, 300)
Cost time:10.196919679641724s
(400, 400)
Cost time:15.698249101638794s
(500, 500)
Cost time:59.39179468154907s
(600, 600)
Cost time:48.376357078552246s
(700, 700)
Cost time:66.68462252616882s
(800, 800)
Cost time:83.17590832710266s
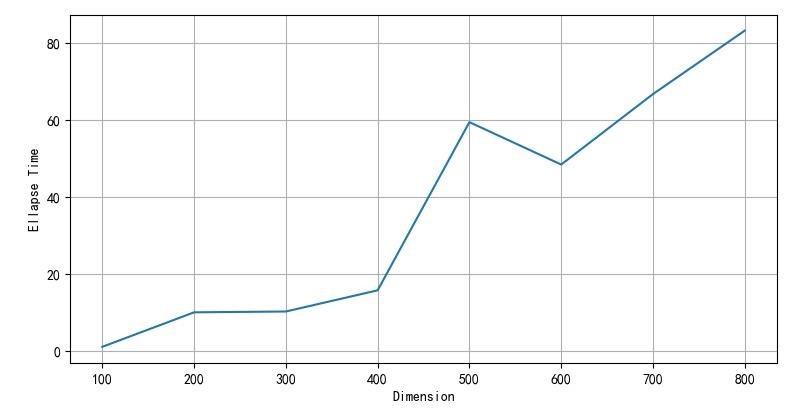
▲ 图1.2.4 数组长度与是求逆时间
2、图片识别
利用在 PaddleHub一键识别动物 : resnet50 测试的Paddle中的resnet50-vd_animals模型。
(1)在基本版本运行时间
在基本版本运行环境中运行时间: 19.1s。
(2)在高级版本运行时间
在高级版本运行时间:17.919s
(3)在至尊版本运行时间
在至尊版本运行环境运行时间:16.4s
※ 测试总结 ※
对比了AI Studio中的三种运行环境。基础版本、高级版本以及至尊版本。它们的配置是越来越高的。通过两种方式进行测试:
- 测试对于大型矩阵求逆;
- 测试resnet50识别动物;
可以看到实际上基础版本程序中,对于矩阵求逆运行速度是最快的。在图像识别中,智尊版本运行时间最快,但三个版本的差别并不是很大。
那么问题来了,这三个环境的配置,难道仅仅说说玩玩的吗?毕竟对于基础版本在使用费用上是没有限制的,而其他两个版本则是要求需要计算卡的呀?
一、补充实验
测试一个AlexNet 识别MNIST的程序。
1、测试程序
import paddle
import paddle.nn.functional as F
class AlexNet(paddle.nn.Layer):
def __init__(self) -> None:
super(AlexNet,self).__init__()
self.conv1 = paddle.nn.Conv2D(in_channels = 1, out_channels = 96, kernel_size = 11, stride = 4)
self.conv2 = paddle.nn.Conv2D(in_channels = 96, out_channels = 256, kernel_size = 5, stride = 1, padding = 2)
self.conv3 = paddle.nn.Conv2D(in_channels = 256, out_channels = 384, kernel_size = 3, stride = 1, padding = 1)
self.conv4 = paddle.nn.Conv2D(in_channels = 384, out_channels = 384, kernel_size = 3, stride = 1, padding = 1)
self.conv5 = paddle.nn.Conv2D(in_channels = 384, out_channels = 256, kernel_size = 3, stride = 1, padding = 1)
self.pool1 = paddle.nn.MaxPool2D(3,2)
self.pool2 = paddle.nn.MaxPool2D(3,2)
self.pool3 = paddle.nn.MaxPool2D(3,2)
self.linear1 = paddle.nn.Linear(in_features = 256*5*5, out_featur以上是关于AI Studio 不同环境下的执行速度的主要内容,如果未能解决你的问题,请参考以下文章