优化算法多目标哈里斯鹰优化算法（MOHHO）含Matlab源码 1596期

Posted 2022-01-03 紫极神光

一、获取代码方式

获取代码方式1：
完整代码已上传我的资源：【优化算法】多目标哈里斯鹰优化算法（MOHHO）【含Matlab源码 1596期】

获取代码方式2：
通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，可获得此代码。

备注：
订阅紫极神光博客付费专栏，可免费获得1份代码（有效期为订阅日起，三天内有效）；

二、哈里斯鹰算法简介

HHO算法用数学公式来模拟现实中哈里斯鹰在不同机制下捕捉猎物的策略.在HHO中，哈里斯鹰是候选解，猎物随迭代逼近最优解.HHO算法包括两个阶段：全局探索阶段、局部开采阶段。
1 全局探索阶段
在这一阶段中，哈里斯鹰处于等待状态，仔细检查和监控搜索空间[lb,ub]以发现猎物.它根据两种策略在随机的地方寻找猎物，迭代时以概率q进行位置更新，数学表达式为：

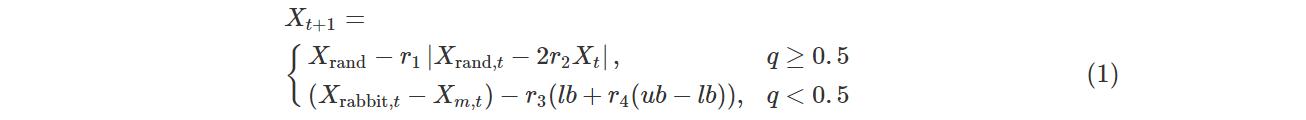
式中，Xt+1和Xt分别为哈里斯鹰第t+1次和第t次迭代时的位置，Xrabbit, t表示猎物第t次迭代时的位置，q和r1,r2,r3,r4是区间(0,1)内的随机数字，lb是搜索空间的下界，ub是搜索空间的上界，Xrand, t表示第t次迭代时哈里斯鹰的随机位置，Xm,t表示第t次迭代时哈里斯鹰的平均位置，公式如下：

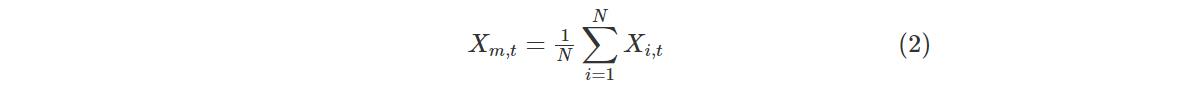
2 过渡阶段
任何群智能算法的精确运行，需要保持探索和开采之间适当的平衡.HHO通过猎物的能量方程实现从探索到开采的过渡，其模型如下：

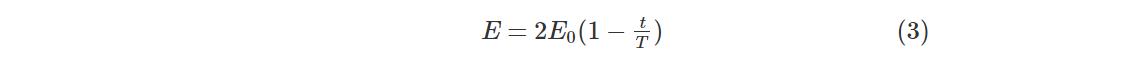
式中，E表示猎物逃跑的能量，E0是猎物能量的初始状态，公式为E0=2*rand-1,rand是(0,1)之间的随机数字，T为最大迭代次数，t为当前迭代次数.当|E|≥1时，哈里斯鹰算法将执行全局探索；否则，HHO算法进入局部开采.

3 局部开采阶段

在这一阶段，哈里斯鹰根据前一阶段的检测执行突袭攻击预期猎物，而猎物试图逃离危险.根据猎物的逃跑行为和哈里斯鹰的追逐策略，HHO算法提出了四种可能的策略来模拟攻击行为.用λ表示猎物成功逃脱的概率，当λ<0.5时，猎物逃脱成功；当λ≥0.5时，猎物逃脱失败.用参数E模拟哈里斯鹰软或硬的围攻策略.当|E|≥0.5时，执行软围攻；否则，执行硬围攻.
Case1:软围攻.当|E|≥0.5,λ≥0.5时，猎物有足够的能量且以跳跃的方式逃脱围捕，而哈里斯鹰会逐渐消耗猎物的能量，然后选择最佳的位置突袭俯冲逮捕猎物.更新位置的方程如下：

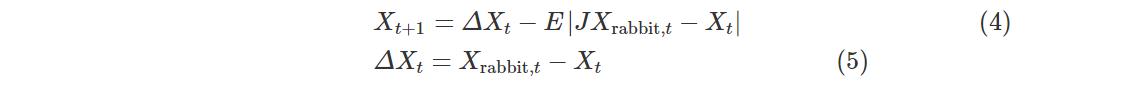
式中，Xt是迭代时猎物与哈里斯鹰的位置之差，J=2(1-r5)表示猎物逃跑过程中的随机跳跃，r5是介于0到1之间的随机数字.

Case2:硬围攻.当|E|<0.5,λ≥0.5时，猎物筋疲力尽，哈里斯鹰选择迅速突袭.位置更新如下：

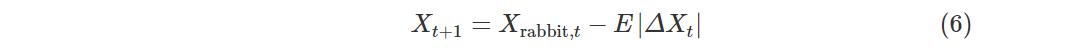
Case3:累速俯冲式软围攻.当|E|≥0.5,λ<0.5时，猎物有足够的能量E逃跑，哈里斯鹰在突袭之前会建立一个软围攻.为了模拟猎物的逃跑模式和跳跃动作，将levy函数LF集成在HHO算法中.更新位置的策略为：

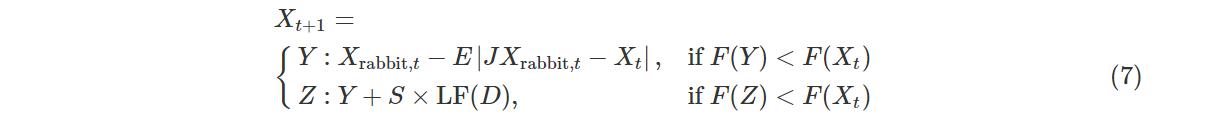
式中，D为问题维度，S为D维随机行向量.

Case4:累速俯冲式硬围攻.当|E|<0.5,λ<0.5时，猎物能量E低，哈里斯鹰在突袭前构建硬围攻捕捉猎物，位置更新如下：

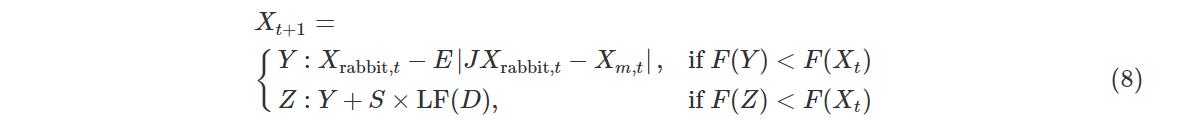
HHO算法用猎物能量E和因子λ调节哈里斯鹰和猎物(兔子)之间的四种围捕机制，来实现优化求解问题。

三、部分源代码

clc;
clear;
close all;

%% Problem Definition

CostFunction=@(x) CostFunction(x);      % Cost Function

nVar=5;             % Number of Decision Variables

VarSize=[1 nVar];   % Size of Decision Variables Matrix

VarMin=0;          % Lower Bound of Variables
VarMax=1;          % Upper Bound of Variables


%% MOPSO Parameters

MaxIt=200;           % Maximum Number of Iterations

nPop=200;            % Population Size

nRep=50;            % Repository Size

w=0.5;              % Inertia Weight
wdamp=0.99;         % Intertia Weight Damping Rate
c1=1;               % Personal Learning Coefficient
c2=2;               % Global Learning Coefficient

nGrid=7;            % Number of Grids per Dimension
alpha=0.1;          % Inflation Rate

beta=2;             % Leader Selection Pressure
gamma=2;            % Deletion Selection Pressure

mu=0.1;             % Mutation Rate

%% Initialization

empty_Rabbit.Location=[];
empty_Rabbit.Cost=[];
empty_Rabbit.Sol=[];
empty_Rabbit.IsDominated=[];
empty_Rabbit.GridIndex=[];
empty_Rabbit.GridSubIndex=[];

Rabbits=repmat(empty_Rabbit,nPop,1);
X = zeros(nPop, nVar);
Rabbit_Location=zeros(VarSize);
Rabbit_Energy=inf;

for i=1:nPop
    
    Rabbits(i).Location = rand(VarSize).*(VarMax-VarMin)+VarMin; 
    X(i,:) = rand(VarSize).*(VarMax-VarMin)+VarMin; 
    [Rabbits(i).Cost, Rabbits(i).Sol] = CostFunction(Rabbits(i).Location);
    
end

% Determine Domination
Rabbits=DetermineDomination(Rabbits);

rep=Rabbits(~[Rabbits.IsDominated]);

Grid=CreateGrid(rep,nGrid,alpha);

for i=1:numel(rep)
    rep(i)=FindGridIndex(rep(i),Grid);
end


%% MOPSO Main Loop

for it=1:MaxIt
    E1=2*(1-(it/MaxIt)); % factor to show the decreaing energy of rabbit    
    for i=1:nPop
        
        leader=SelectLeader(rep,beta);
        
        
        E0=2*rand()-1; %-1<E0<1
        Escaping_Energy=E1*(E0);  % escaping energy of rabbit
        
        if abs(Escaping_Energy)>=1
            %% Exploration:
            % Harris' hawks perch randomly based on 2 strategy:
            
            q=rand();
            rand_Hawk_index = floor(nPop*rand()+1);
            X_rand = Rabbits(rand_Hawk_index);
            if q<0.5
                % perch based on other family members
                Rabbits(i).Location=X_rand.Location-rand()*abs(X_rand.Location-2*rand()*Rabbits(i).Location);
                X(i,:)=X_rand.Location-rand()*abs(X_rand.Location-2*rand()*Rabbits(i).Location);
            elseif q>=0.5
                % perch on a random tall tree (random site inside group's home range)
                Rabbits(i).Location=(leader.Location-mean(X))-rand()*((VarMax-VarMin)*rand+VarMin);
                X(i,:)=(leader.Location-mean(X))-rand()*((VarMax-VarMin)*rand+VarMin);
            end
            
        elseif abs(Escaping_Energy)<1
            %% Exploitation:
            % Attacking the rabbit using 4 strategies regarding the behavior of the rabbit
            
            %% phase 1: surprise pounce (seven kills)
            % surprise pounce (seven kills): multiple, short rapid dives by different hawks
            
            r=rand(); % probablity of each event
            
            if r>=0.5 && abs(Escaping_Energy)<0.5 % Hard besiege
                Rabbits(i).Location=(leader.Location)-Escaping_Energy*abs(leader.Location-Rabbits(i).Location);
                X(i,:)=(leader.Location)-Escaping_Energy*abs(leader.Location-X(i,:));
            end
            
            if r>=0.5 && abs(Escaping_Energy)>=0.5  % Soft besiege
                Jump_strength=2*(1-rand()); % random jump strength of the rabbit
                X(i,:)=(leader.Location-X(i,:))-Escaping_Energy*abs(Jump_strength*Rabbit_Location-X(i,:));
                Rabbits(i).Location=(leader.Location-Rabbits(i).Location)-Escaping_Energy*abs(Jump_strength*Rabbit_Location-Rabbits(i).Location);
            end
            
            %% phase 2: performing team rapid dives (leapfrog movements)
            if r<0.5 && abs(Escaping_Energy)>=0.5 % Soft besiege % rabbit try to escape by many zigzag deceptive motions
                
                Jump_strength=2*(1-rand());
                X1.Location=leader.Location-Escaping_Energy*abs(Jump_strength*leader.Location-X(i,:));
                [X1.Cost, X1.Sol] = CostFunction(X1.Location);
                if Dominates(X1,Rabbits(i))
                    Rabbits(i).Location=X1.Location;
                    Rabbits(i).Cost=X1.Cost;
                    Rabbits(i).Cost=X1.Cost;

                elseif Dominates(Rabbits(i),X1)
                    X2.Location=leader.Location-Escaping_Energy*abs(Jump_strength*leader.Location-X(i,:))+rand(1,nVar).*Levy(nVar);                    
                    [X2.Cost, X2.Sol] = CostFunction(X2.Location);
                    if Dominates(X2,Rabbits(i))
                        Rabbits(i).Location=X2.Location;
                        Rabbits(i).Cost=X2.Cost;
                        Rabbits(i).Cost=X2.Cost;
                    end
                else
                    if rand<0.5
                        Rabbits(i).Location=X1.Location;
                        Rabbits(i).Cost=X1.Cost;
                        Rabbits(i).Cost=X1.Cost;
                        Rabbits(i).Sol=X1.Sol;
                    end
                end                                
            end
            
            if r<0.5 && abs(Escaping_Energy)<0.5 % Hard besiege % rabbit try to escape by many zigzag deceptive motions
                % hawks try to decrease their average location with the rabbit
                Jump_strength=2*(1-rand());
                X1.Location=leader.Location-Escaping_Energy*abs(Jump_strength*leader.Location-mean(X));
                [X1.Cost, X1.Sol] = CostFunction(X1.Location);
                if Dominates(X1,Rabbits(i))
                    Rabbits(i).Location=X1.Location;
                    Rabbits(i).Cost=X1.Cost;
                    Rabbits(i).Cost=X1.Cost;

                elseif Dominates(Rabbits(i),X1)
                    X2.Location=leader.Location-Escaping_Energy*abs(Jump_strength*leader.Location-mean(X))+rand(1,nVar).*Levy(nVar);                    
                    [X2.Cost, X2.Sol] = CostFunction(X2.Location);
                    if Dominates(X2,Rabbits(i))
                        Rabbits(i).Location=X2.Location;
                        Rabbits(i).Cost=X2.Cost;
                        Rabbits(i).Cost=X2.Cost;
                    end
                else
                    if rand<0.5
                        Rabbits(i).Location=X1.Location;
                        Rabbits(i).Cost=X1.Cost;
                        Rabbits(i).Cost=X1.Cost;
                        Rabbits(i).Sol=X1.Sol;
                    end
                end                               
            end
        end
        

四、运行结果

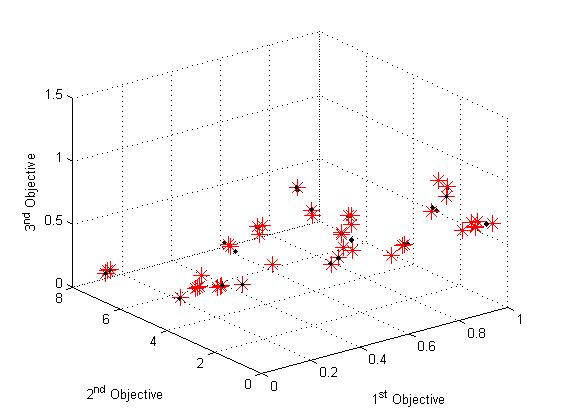
五、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.