LeetCodeLeetCode之跳跃游戏——动态规划+贪心算法

Posted 2022-01-03 Roninaxious

【LeetCode】LeetCode之打家劫舍【暴力递归、动态规划、动态规划之优化空间的具体分析与实现】	https://blog.csdn.net/Kevinnsm/article/details/121838892?spm=1001.2014.3001.5501
【LeetCode】LeetCode之打家劫舍Ⅱ——暴力递归+动态规划解决循环问题+DP空间优化	https://blog.csdn.net/Kevinnsm/article/details/121813241?spm=1001.2014.3001.5501
【LeetCode】LeetCode之删除并获得点数——动态规划、排序+动态规划	https://blog.csdn.net/Kevinnsm/article/details/121838892?spm=1001.2014.3001.5501

1.题目描述

给定一个非负整数数组 nums ，你最初位于数组的 第一个下标 。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标。(nums.length>0)

🥩示例 1：

输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。

🥩示例 2：

输入：nums = [3,2,1,0,4]
输出：false
解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标。

2.思路分析

这种问题首先能够想到的肯定是能否使用动态规划，不要问为什么，问就说做的多了。

首先做动态规划这一类的题，首先要考虑的是如何将原分解成一个个的小问题。

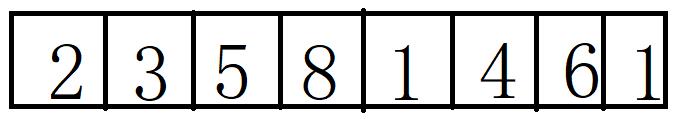
例如上述n=8的一个nums数组，分析流程如下：

• Ⅰ.如果我要求f(8)【8号位置是不是可达的】，是不是我只需要判断f(7)是否是可达以及f(7)+7 >= 8【f(7)>=1】；
• Ⅱ.对于Ⅰ中我们核心要求f(7)是否可达，是不是意味着只需要判断f(6)是否可达以及f(6)+6 >= 7，也就是f(6)>=1.

所以该子问题分解成功！此时状态转移方程也就推导出来了。【下图0也可达，写错了！】

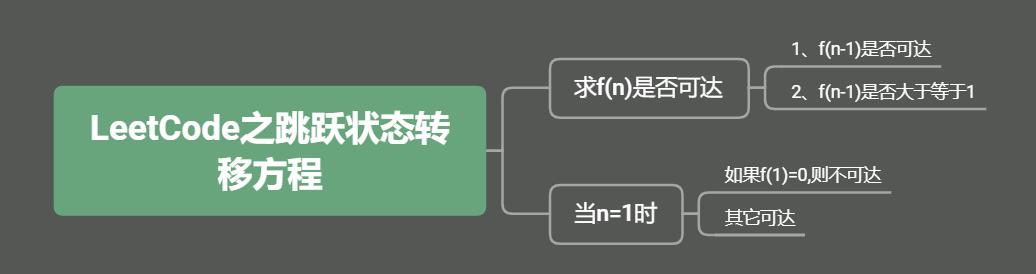
3.动态规划解题代码及其分析

    public boolean canJump2(int[] nums) 
        if (nums.length == 1) 
            return true;
        
        boolean[] dp = new boolean[nums.length];
        dp[0] = true;
        for (int i = 1; i < nums.length; i++) 
            for (int j = 0; j < i; j++) 
                if (dp[j] && nums[j] + j >= i) 
                    dp[i] = true;
                    break;
                
            
        
        return dp[nums.length - 1];
    

提交到LeetCode时，发现执行时间高达772ms。

复杂度分析

时间复杂度：O(n^2)
空间复杂度：O(n)

4.贪心思路分析

在上述动态规划的分析中，我们会发现使用动态规划无法达到比较好的效果。因为动态规划的解要依赖子问题的解，仔细想一下你就会发现本题中有可能某个数据会一步到达最后，也就是可以进行跳跃。

所以我们可以利用贪心思想，对数组进行遍历，在这个遍历过程中维护一个最远距离；一旦这个最远距离大于nums.length-1，直接返回true即可。

代码实现

    public boolean canJump4(int[] nums) 
        int size = nums.length;
        int maxFar = nums[0];
        for (int i = 0; i < size; i++) 
            if (maxFar >= i) 
                maxFar = Math.max(maxFar, nums[i] + i);
                if (maxFar >= size - 1) 
                    return true;
                
            
        
        return false;
    

当我提交到LeetCode时如图所示。

复杂度分析

时间复杂度：O(n)
空间复杂度：O(1)

相比较使用时动态规划有了巨大的提升。