隐马尔科夫模型（HMM）解决命名实体识别问题（NER）

Posted 2022-01-03 Unstoppable~~~

一、命名实体识别介绍

命名实体识别(英语:Named Entity Recognition，简称NER)是指识别文本中具有特定意义的实体，主要包括人名、地名、机构名、专有名词等等，并把我们需要识别的词在文本序列中标注出来。
例如有一段文本:济南市成立自由贸易试验区.
我们要在上面文本中识别一些区域和地点,那么我们需要识别出来内容有:
济南市(地点),自由贸易试验区(地点).
在我们今天使用的NER数据集中,一共有7个标签（每个字都要对应一个标签，标签前缀B表示当前字为实体的第一个字begin，I表示实体除第一个以外的字，也就是内部的字in）:

序号	标签	含义
1	B-ORG	组织或公司(organization)
2	I-ORG	组织或公司(organization)
3	B-PER	人名(person)
4	I-PER	人名(person)
5	O	其他非实体(other)
6	B-LOC	地名(location)
7	I-LOC	地名

比如说"自贸区"对应的标注是:自(B-LOC)贸(I-LOC)区(1I-LOC),这三个字都对应一个"地名"的标签,但是第一个字属于实体开头的字,所以使用"B"开头的标签,后面两个字的标签都是"I"开头.

二、隐马尔可夫模型介绍HMM

HMM模型是概率图模型的一种,属于生成模型,笼统的说,我们上面说的"BIO"的实体标签,就是一个不可观测的隐状态,而HMM模型描述的就是由这些隐状态序列(实体标记)生成可观测结果(可读文本)的过程.
在我们今天的问题当中,隐状态序列是实体标记序列,而可观测序列是我们可读的原始语料文本序列.
以“自贸区”为例：
隐藏状态序列：B-LOC | I-LOC | I-LOC
观测结果序列： 自 | 贸 | 区

隐马尔可夫模型的示意图如下所示;

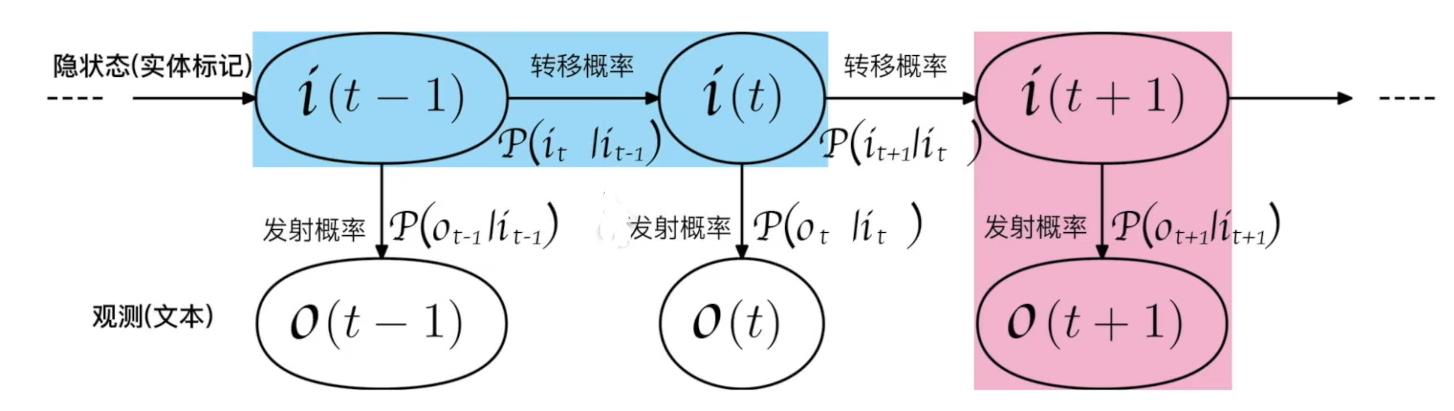
HMM 的定义建立在两个基本假设的前提上，这两个假设是 HMM 的重点，一定要了解模型的 2 个假设。
1）齐次马尔科夫假设
齐次马尔科夫假设，通俗地说就是 HMM 的任一时刻 t 的某一状态只依赖于其前一时刻的状态，与其它时刻的状态及观测无关，也与时刻 t 无关。
2）观测独立假设
观测独立性假设，是任一时刻的观测只依赖于该时刻的马尔科夫链的状态，与其他观测及状态无关。
以上这两个假设是 HMM 的核心，之后的公式推导都是依赖这两个假设成立的基础上进行的。

三、隐马尔可夫模型三个重要参数

1.HMM的状态转移概率
我们上面提到了P(I(t)|I(t-1))指的是隐状态i从t一1时刻转向t时刻的概率,比如说我们现在实体标签一共有7种,也就是N =7(注意N是所有可能的实体标签种类的集合),也就是Qhidden = qo q1…,q6(注意我们实体标签编号从O算起),假设在t -1时刻任何一种实体标签都可以在t时刻转换为任何一种其他类型的实体标签,则总共可能的转换的路径一共有NN种,所以我们可以做一个NN的矩阵来表示所有可能的隐状态转移概率.

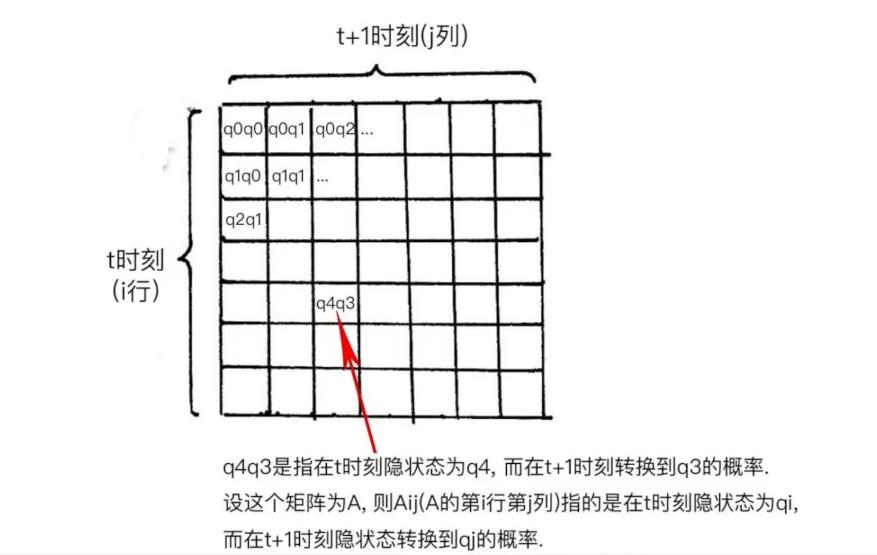
2.HMM的发射概率
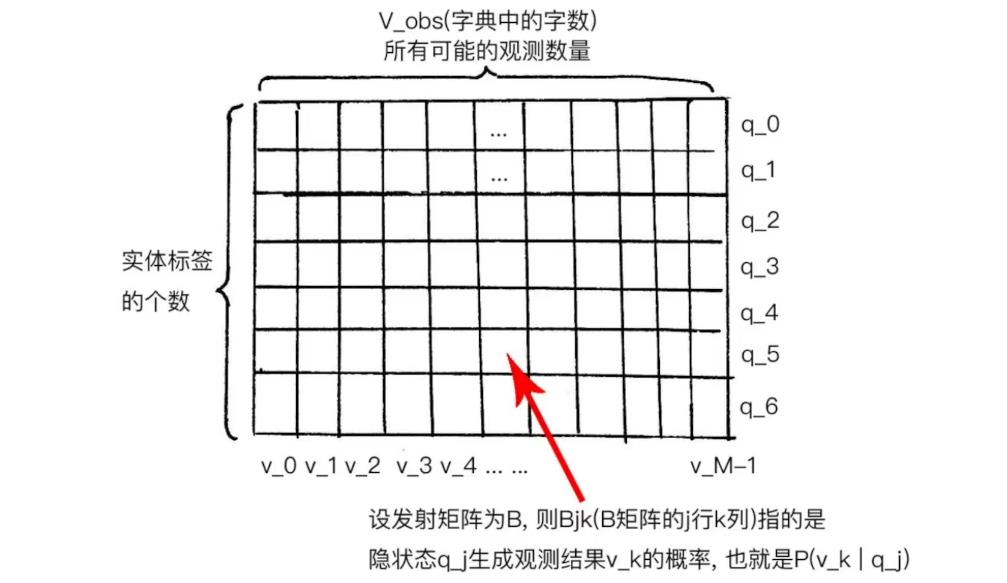
我们之前提到了任意时刻观测Ｏt,只依赖于当前时刻的隐状态It，也就是P(O(t)|I(t))，也叫做发射概率,指的是隐状态生成观测结果的过程.设我们的字典里有M个字,Vobs.= v(0), v(1),…,v(m-1)(注意这里下标从0算起,所以最后的下标是m-1，一共有m种观测),则每种实体标签(隐状态)可以生成m种不同的汉字(也就是观测),这一过程可以用一个发射概率矩阵来表示,他的维度是N*M.

3.HMM初始隐状态概率

四、隐马尔可夫模型的参数估计

Π的计算可以理解为qi在第一个字的次数/总次数

A的计算可以理解为qi转移到qj的次数/qi出现的总次数

B的计算可以理解为 qi和Vk同时出现的次数/qj出现的次数

五、维特比算法

维特比算法viterbi algorithm使用了动态规划算法来解决类似HMM和CRF的预测问题,
用维特比算法可以找到概率最大路径，也就是最优路径，在我们今天要解决的序列标注问题中，就要通过维特比算法,来找到文本所对应的最优的实体标注序列.
如果用一句话来概括维特比算法,那就是:
在每一时刻,计算当前时刻落在每种隐状态的最大概率，并记录这个最大概率是从前一时刻哪个隐状态转移过来的，最后再从结尾回溯最大概率，最终得到最大概率路径，也就是最优路径
可以用下图（有向无环图）表示维特比算法的每个状态及最大概率关系：

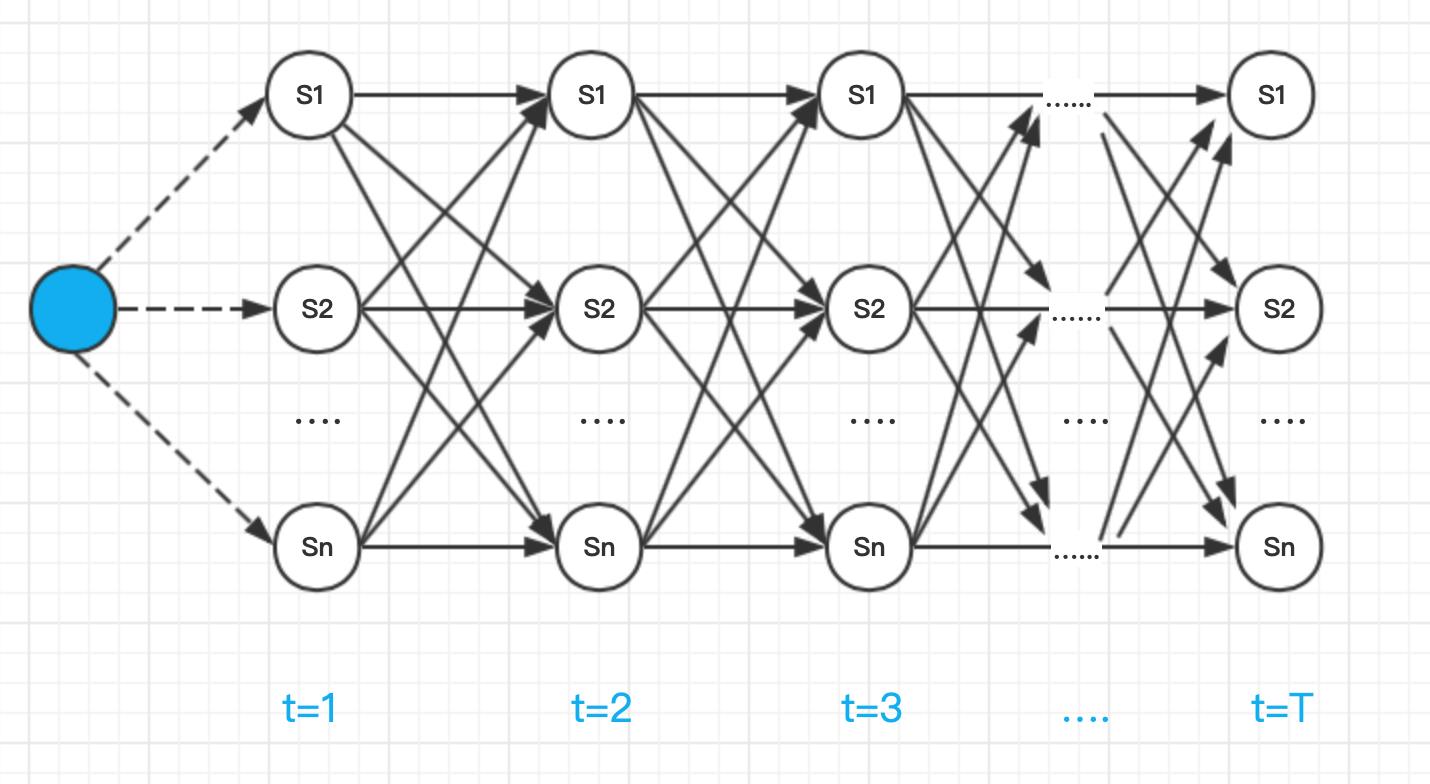
上图从左往右时序递增，虚线由初始状态概率决定，实线则是转移概率。由于受到观测序列的约束，不同状态发射观测的概率不同，所以每个节点本身也必须计算自己的花费，由发射概率决定。又由于 Yt+1 仅依赖于 Yt，所以网状图可以动态规划的搜索，也就是维特比算法

1.初始化，t=1 时初始最优路径的备选由 N 个状态组成，它们的前驱为空。

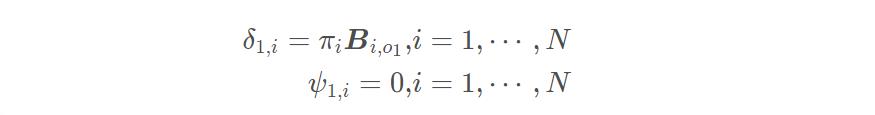
其中，δ 存储在时刻 t 以 Si 结尾的所有局部路径的最大概率。ψ 存储局部最优路径末状态 Yt 的前驱状态。

2.递推，t >= 2 时每条备选路径像贪吃蛇一样吃入一个新状态，长度增加一个单位，根据转移概率和发射概率计算花费。找出新的局部最优路径，更新 δ、ψ 两个数组

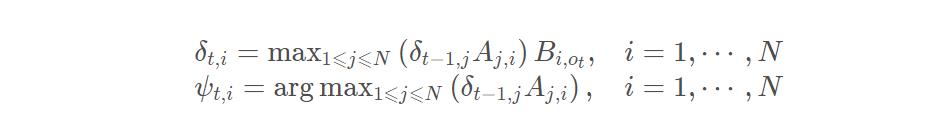
3.终止，找出最终时刻 δt,i 数组中的最大概率 P*，以及相应的结尾状态下标 i*t。

4.回溯，根据前驱数组 ψ 回溯前驱状态，取得最优路径状态下标。

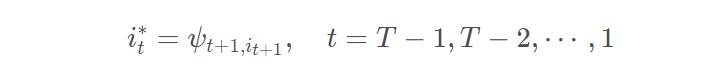
六、代码实现

利用训练数据获取HMM模型对应的参数A，B和Pi

""" HMM 参数构建 """
import numpy as np
# N: 状态数，这里对应存在的标注的种类 
# M: 观测数，这里对应有多少不同的字
N, M = len(tag2id), len(word2id)
# 状态转移概率矩阵 A[i][j]表示从i状态转移到j状态的概率
A = np.zeros(shape=(N, N), dtype=float)
# 观测概率矩阵, B[i][j]表示i状态下生成j观测的概率
B = np.zeros(shape=(N, M), dtype=float)
# 初始状态概率  Pi[i]表示初始时刻为状态i的概率
Pi = np.zeros(shape=N, dtype=float)

""" 构建转移概率矩阵 """
for tag_list in train_tag_lists:
    seq_len = len(tag_list)
    for i in range(seq_len - 1):
        current_tagid = tag2id[tag_list[i]]
        next_tagid = tag2id[tag_list[i+1]]
        A[current_tagid][next_tagid] += 1
A[A == 0.] = 1e-10  # 平滑处理
A = A / np.sum(a=A, axis=1, keepdims=True)

""" 构建观测概率矩阵 """
for tag_list, word_list in zip(train_tag_lists, train_word_lists):
    assert len(tag_list) == len(word_list)
    for tag, word in zip(tag_list, word_list):
        tag_id = tag2id[tag]
        word_id = word2id[word]
        B[tag_id][word_id] += 1
B[B == 0.] = 1e-10  # 平滑处理
B = B / np.sum(a=B, axis=1, keepdims=True)

""" 构建初始状态概率 """
for tag_list in train_tag_lists:
    init_tagid = tag2id[tag_list[0]]
    Pi[init_tagid] += 1
Pi[Pi == 0.] = 1e-10  # 平滑处理
Pi = Pi / np.sum(a=Pi)

""" 维特比算法 """
def viterbi(word_list, word2id, tag2id):
    """
    使用维特比算法对给定观测序列求状态序列， 这里就是对字组成的序列,求其对应的标注。
    维特比算法实际是用动态规划解隐马尔可夫模型预测问题，即用动态规划求概率最大路径（最优路径）
    这时一条路径对应着一个状态序列
    """
    # 问题:整条链很长的情况下，十分多的小概率相乘，最后可能造成下溢
    # 解决办法：采用对数概率，这样源空间中的很小概率，就被映射到对数空间的大的负数
    #  同时相乘操作也变成简单的相加操作
    ALog = np.log(A)
    BLog = np.log(B)
    PiLog = np.log(Pi)

    # 初始化 维比特矩阵viterbi 它的维度为[状态数, 序列长度]
    # 其中viterbi[i, j]表示标注序列的第j个标注为i的所有单个序列(i_1, i_2, ..i_j)出现的概率最大值
    seq_len = len(word_list)
    viterbi = np.zeros(shape=(N, seq_len), dtype=float)
    # backpointer是跟viterbi一样大小的矩阵
    # backpointer[i, j]存储的是 标注序列的第j个标注为i时，第j-1个标注的id
    # 等解码的时候，我们用backpointer进行回溯，以求出最优路径
    backpointer = np.zeros(shape=(N, seq_len), dtype=float)

    # Pi[i] 表示第一个字的标记为i的概率
    # Bt[word_id]表示字为word_id的时候，对应各个标记的概率
    # A.t()[tag_id]表示各个状态转移到tag_id对应的概率

    # 所以第一步为
    start_wordid = word2id.get(word_list[0], None)
    Bt = BLog.T
    if start_wordid is None:
        # 如果字不再字典里，则假设状态的概率分布是均匀的
        bt = np.log(np.ones(shape=N, dtype=float) / N)
    else:
        bt = Bt[start_wordid]
    viterbi[:, 0] = PiLog + bt
    backpointer[:, 0] = -1

    # 递推公式：viterbi[tag_id, step] = max(viterbi[:, step-1]* A.t()[tag_id] * Bt[word])
    # 其中word是step时刻对应的字, 由上述递推公式求后续各步
    for step in range(1, seq_len):
        wordid = word2id.get(word_list[step], None)
        # 处理字不在字典中的情况
        # bt是在t时刻字为wordid时，状态的概率分布
        if wordid is None:
            # 如果字不再字典里，则假设状态的概率分布是均匀的
            bt = np.log(np.ones(N) / N)
        else:
            bt = Bt[wordid]  # 否则从观测概率矩阵中取bt
        for tag_id in range(len(tag2id)):
            max_prob = np.max(a=viterbi[:, step - 1] + ALog[:, tag_id], axis=0)
            max_id = np.argmax(a=viterbi[:, step - 1] + ALog[:, tag_id], axis=0)
            viterbi[tag_id, step] = max_prob + bt[tag_id]
            backpointer[tag_id, step] = max_id

    # 终止， t=seq_len 即 viterbi[:, seq_len]中的最大概率，就是最优路径的概率
    best_path_prob = np.max(a=viterbi[:, seq_len - 1], axis=0)
    best_path_pointer = np.argmax(a=viterbi[:, seq_len - 1], axis=0)

    # 回溯，求最优路径
    best_path_pointer = int(best_path_pointer)
    best_path = [best_path_pointer]

    for back_step in range(seq_len-1, 0, -1):
        best_path_pointer = backpointer[best_path_pointer, back_step]
        best_path_pointer = int(best_path_pointer)
        best_path.append(best_path_pointer)

    # 将tag_id组成的序列转化为tag
    assert len(best_path) == len(word_list)
    id2tag = dict((id_, tag) for tag, id_ in tag2id.items())
    tag_list = [id2tag[id_] for id_ in reversed(best_path)]

    return tag_list

""" 利用HMM识别ner_char_data目录下test.txt中的数据"""
pred_tag_lists = []
for word_list in test_word_lists:
    pred_tag_list = viterbi(word_list, word2id, tag2id)
    pred_tag_lists.append(pred_tag_list)

""" HMM 评测 """
from evaluating import Metrics
metrics = Metrics(test_tag_lists, pred_tag_lists, remove_O=False)
metrics.report_scores()
metrics.report_confusion_matrix()