《算法:一解通全》双指针篇——一篇解破ㄈ双指针技巧」
Posted 0_uL<解题者1
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了《算法:一解通全》双指针篇——一篇解破ㄈ双指针技巧」相关的知识,希望对你有一定的参考价值。
前言:【双指针】是通过两个变量交替相向/相对移动完成任务的算法,在数组、链表相关问题上频频出现。下面,让我们逐步看清双指针

破解索引:
1.什么是双指针?⋙
不少C/C++选手初看到“双指针”这三字常常会心生疑惑,尤其是C选手,初见时,往往会不经意联想到二级指针。
而这里的双指针和“指针”不是同一回事,这里的双指针或许叫做“双下标”、“双索引”更适合。
双指针是通过通过两个变量交替相向/相对移动求解问题的算法,具体可分为【1️⃣左右指针,相对移动】和【2️⃣快慢指针,同向移动】
下面具体来看这两种双指针的使用技巧
2.左右(对撞)指针常用技巧⋙
左、右指针一般用在数组问题里面,实际上指的是两个索引值,一般初始化为left=0,right=arr.size()-1
【1】二分搜索
下面来看最简单的二分搜索模板👇
nt binarySearch(vector<int>& nums, int target)
if(nums.size() == 0)
return -1;
int left = 0, right = nums.size() - 1;
while(left <= right)
// 防止(left + right) 溢出👇
int mid = left + (right - left) / 2;
if(nums[mid] == target) return mid;
else if(nums[mid] < target) left = mid + 1;
else right = mid - 1;
// 结束条件: left > right
return -1;

【2】判断回文串
给定一个字符串,验证它是否是回文串,只考虑字母和数字字符,可以忽略字母的大小写。
bool isPalindrome(string s)
int left=0;
int right=s.size()-1;
while(left<right) //两边对撞
if(s[left]!=s[right])return false;//如果不等,则直接返回false
left++;
right--;
return true;
例如:
第一步:最开始指针left指向的字符”c“与指针right指向的字符”c“是一样的。

第二步:指针left向右继续移动一位,指针right向左继续移动一位,考察下一对字符。
同理,这时指针left指向的字符”a“与指针right指向的字符”a“是一样的。
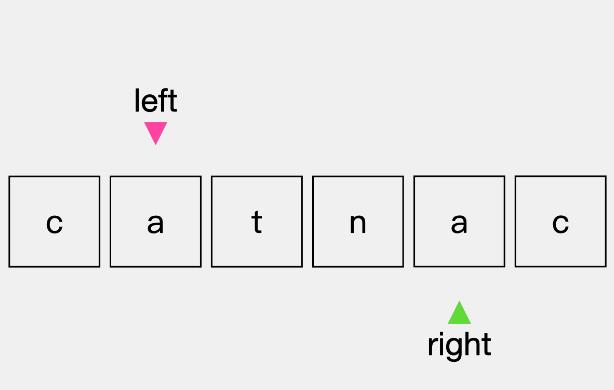
第三步:因此指针left向右继续移动一位,指针right向左继续移动一位,考察下一对字符。
这时,指针left指向的字符”t“与right指向的字符”n“是不同的,也就是说字符串"catnac"不是回文串。至此,即使有剩余的字符也就不需要考虑了。

同样:判断回文数可以先通过to_string将其转化为字符串再进行如上判断
【3】反转数组
👻一般的编程语言都会提供反转数组的接口(函数),不过我们还是要了解这个简单的小轮子是怎么实现的。
void reverse(vector<int>& nums)
int left=0;
int right=nums.size()-1;
while(left<right)
//交换nums[left]和nums[right]
int tmp=nums[left];
nums[left]=nums[right];
nums[right]=tmp;
left++;
right--;
以反转字符串"hello"为例

3.快慢(同步)指针常用技巧⋙
快慢指针一般会初始化指向链表的头结点head,前进时快指针fast在前,慢指针slow在后。
快、慢指针的速度差往往相同。
【1】判断链表中是否含有环
判断单链表是否有环,最简单的方法之一就是用快慢指针,
一个跑得快,一个跑得慢。如果跑得快的那个最终遇到NULL,说明链表不含有环;如果含有环,则快指针最终必会超慢指针一圈,并与它相遇。
犹如环形跑道上竞走的跑者
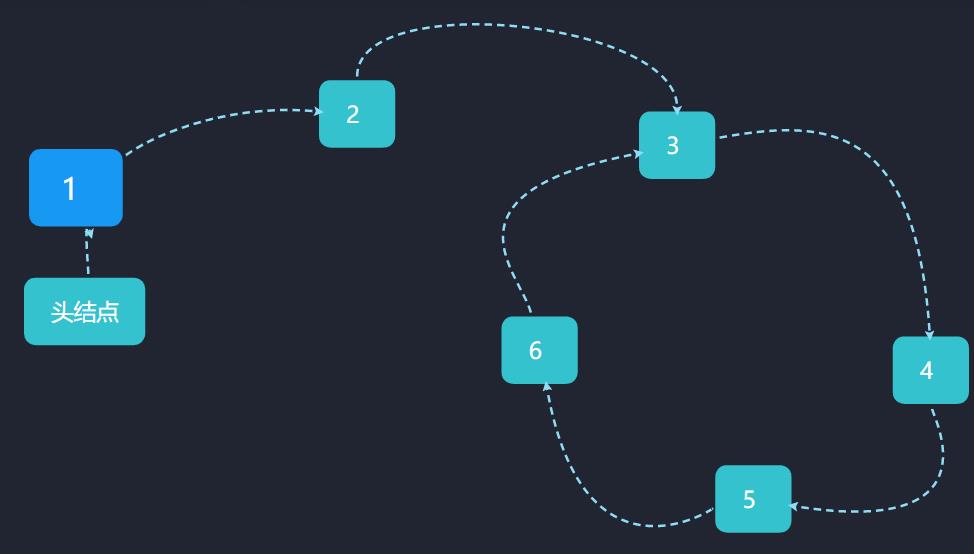
代码实现:
bool hasCycle(ListNode* head)
ListNode* fast=head;
ListNOde* slow=head;
while(fast!=nullptr&&fast->next!=nullptr)
//快指针每次跑两步
fast=fast->next->next;
//慢指针每次跑一步
slow=slow->next;
if(fast==slow)return true;//如果存在环,则快慢指针必相遇
return false;
【2】链表无环返回NULL,若有环则返回这个环的起始节点。

代码实现:
ListNode *detectCycle(ListNode *head)
ListNode* fast=head;
ListNode* slow=head;
while(fast!=nullptr&&fast->next!=nullptr)
fast=fast->next->next;
slow=slow->next;
if(fast==slow)break;
//先检验是否有环👇
if(fast==nullptr||fast->next==nullptr)return nullptr;
slow=head;//先把slow指向head
while(slow!=fast)
fast=fast->next;//两指针同速前进
slow=slow->next;
return slow;//两个指针相遇的地方就是环开始的地方
解释:为什么两指针第二次相遇的地方就是环开始的地方:
第一次相遇时,设快指针走了2k步,慢指针走了k步。快指针fast比慢指针正好比slow多走了k步(环的整数倍,分析易知)

设相遇点与环的起点的距离为m,则环的起点与头结点head的距离为k-m,即:从head前进k-m步即可到达环起点
同样,如果从相遇点继续走k-m步,也一定到达环起点
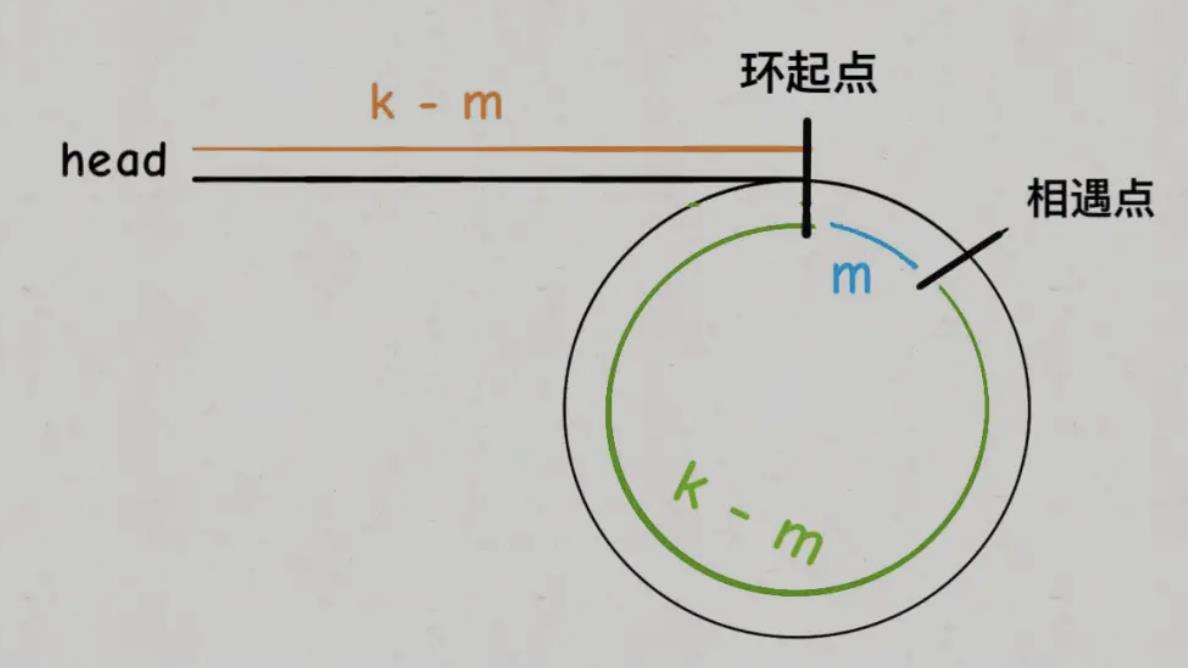
所以,我们只要把快、慢指针中的一个重新指向head,然后两个指针同时同速前进k-m步就会相遇,而这次的相遇点这是我们的目标
【3】寻找无环单链表的中间节点
ListNode* middleNode(ListNode* head)
ListNode* fast=head;
ListNode* slow=head;
while(fast!=nullptr&&fast->next!=nullptr)
fast=fast->next->next;
slow=slow->next;
return slow;
让快指针一次前进两步,慢指针一次前进一步,当快指针到达链表尽头时,慢指针就处于链表的中间位置。
若环长度为奇数,则慢指针恰在链表中心;
为偶数,则慢指针恰在链表中心偏右。
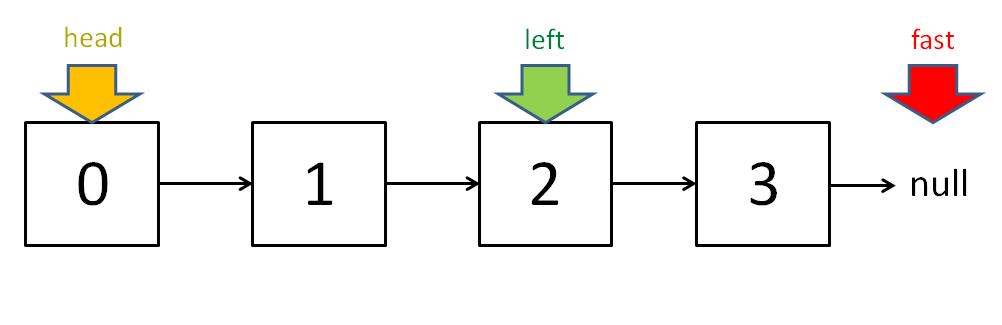
如果有需要找1/3、1/4……的节点,让调整快、慢指针速度的倍数即可
4.总结⋙
- 双指针的最难用法是滑动窗口
我将另做专题研究,尤其是KMP - 不管是【滑动窗口】还是【双指针】,都是基于暴力解法的优化,将时间复杂度降到线性,其实都是在求解中使用一些辅助变量优化
- 这里给出我的建议
- 多多动手画图,辅助分析
- 遇到BUG多多调试,在调试过程中仔细观察双指针是否按我们的想法移动
5.相关题目⋙
以上是关于《算法:一解通全》双指针篇——一篇解破ㄈ双指针技巧」的主要内容,如果未能解决你的问题,请参考以下文章