解题报告《LeetCode零基础指南》(第二讲) 函数
Posted XingleiGao
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了解题报告《LeetCode零基础指南》(第二讲) 函数相关的知识,希望对你有一定的参考价值。

☘前言☘
今天是九日集训第一天,我会记录一下学习内容和题解,争当课代表0.0.
注意!!!!题解的解法一是今天要掌握的解法,解法2是学有余力再研究,涉及到后面知识点0.0
链接:《LeetCode零基础指南》(第二讲) 函数
🧑🏻作者简介:一个从工业设计改行学嵌入式的年轻人
✨联系方式:2201891280(QQ)
⏳全文大约阅读时间: 20min
全文目录
🎁主要知识点梳理
📝力扣的简单使用
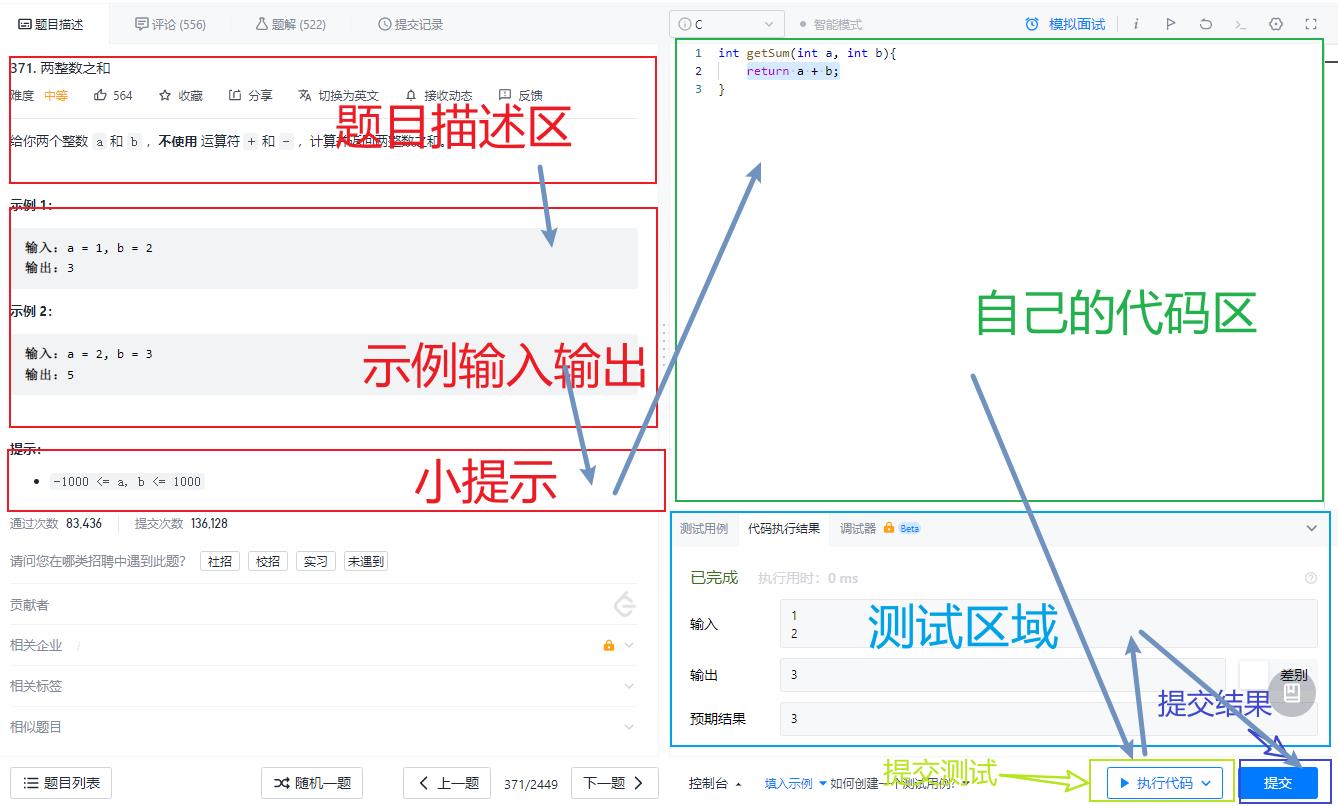
图上我标注了大概的分区,箭头是我的一个做题步骤
就是先看题->观察输入输出->看提示(一定要看,数据范围决定了很多东西)->编码->测试比对结果->提交
📝函数的定义和使用
为了方便理解,我给了一张图,大家应该能看明白。但是我现在有一种思维,就是很多时候函数是叫做接口函数的,那么,为什么叫接口函数呢?
因为如果你将函数看作一个黑匣子,那么你就不需要关注函数的实现,只要给函数对应的值它就会给你返回你要的功能。是不是就像接口一样呀?
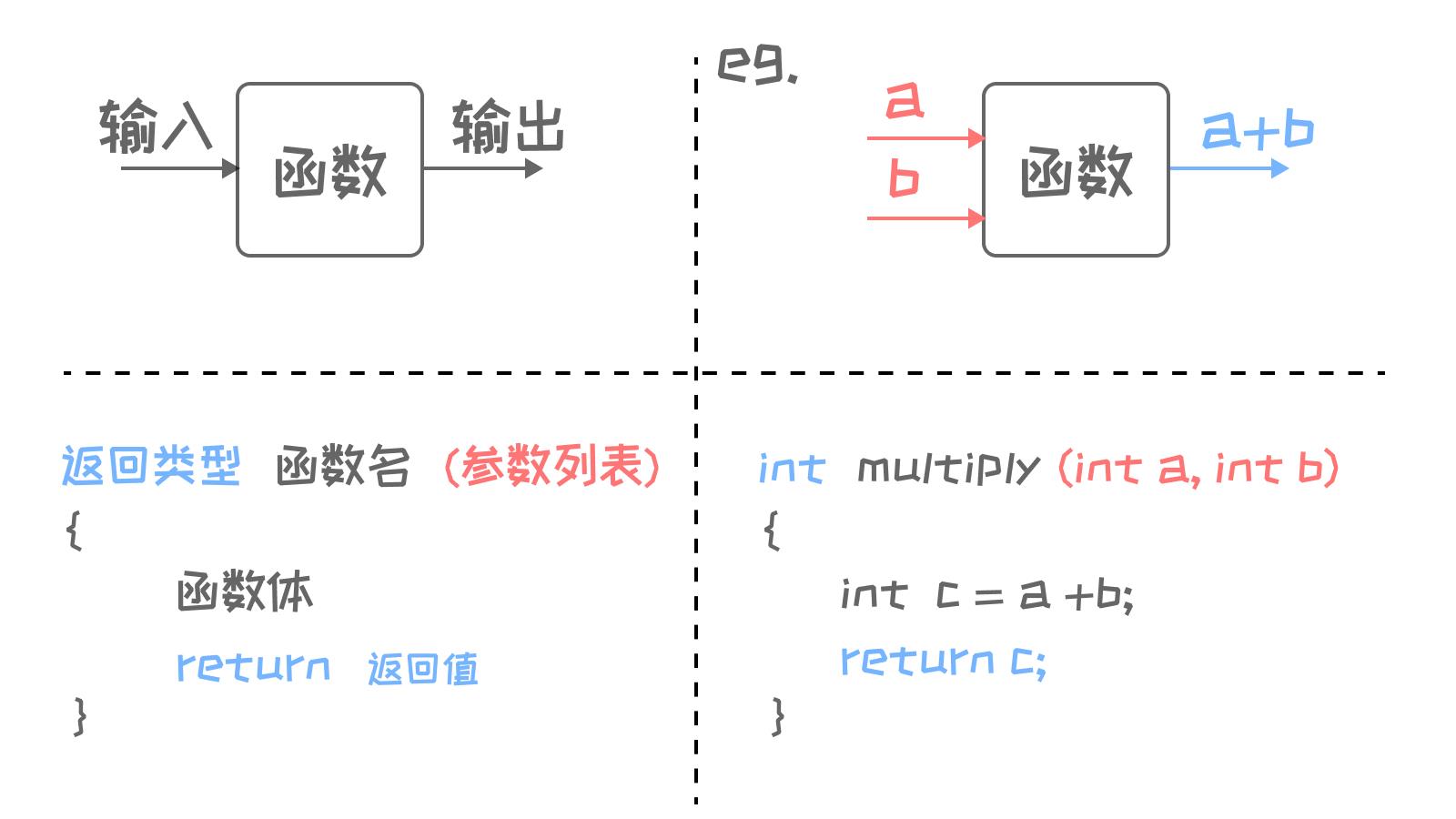
最后是函数的定义和使用 参考图很容易看出来的吧,因为c是一个强类型的语言,所以一定要有对应的类型。我用颜色标出了对应信息,是不是和黑匣子的概念很像呢?
📝内置函数的使用
上一个介绍了函数的定义方式,c语言里面给我们提供了一些内置的函数,今天又几个需要记住的函数,我给大家列出来了。
pow(x,n);// 返回x的n次方 其中x为浮点数
sqrt(x);//返回x的平方根 返回值为浮点数
fmax(a,b);//返回a b中较大的一个。
课后习题详解
371. 两整数之和
371. 两整数之和
面试题 17.01. 不用加号的加法
剑指 Offer 65. 不用加减乘除做加法
这三题是一样的所以就放在一起了
题目描述
给你两个整数 a 和 b ,不使用 运算符 + 和 - ,计算并返回两整数之和。
解题思路1
直接返回a+b就好了。
int getSum(int a, int b)
return a + b;
解题思路2
利用位运算,有一个小知识点,就是半加器其实就是位的异或,全加器是加上了进位,进位的产生是这个位全为1。
int getSum(int a, int b)
while(b)
unsigned int temp = (unsigned int)(a & b) << 1;
//防止溢出要用unsigned int
a = a ^ b;
b = temp;
return a;
面试题 08.05. 递归乘法
题目描述
递归乘法。 写一个递归函数,不使用 * 运算符, 实现两个正整数的相乘。可以使用加号、减号、位移,但要吝啬一些。
解题思路1
别天真,就用乘法就完事了!!
int getSum(int a, int b)
return a * b;
解题思路2
递归乘法有点类似于快速幂的思想,就是看看最低位是否为1
- 如果是的话就+a
- 如果不是就递归调用 a *2 和 b/2。因为整数除法 会舍弃掉余数,所以会有上面的加法。
int multiply(int A, int B)
return (B & 1 ? A : 0) + ((B >> 1) > 0 ? multiply(A<<1,B>>1) : 0);
//返回的其实就是首先判断末位是否为1 然后递归下一层。如果b>>1已经是0了就不需要递归了。
29. 两数相除
题目描述
给定两个整数,被除数
dividend和除数divisor。将两数相除,要求不使用乘法、除法和 mod 运算符。
返回被除数dividend除以除数divisor得到的商。
整数除法的结果应当截去(truncate)其小数部分,例如:truncate(8.345) = 8以及truncate(-2.7335) = -2
解题思路1
别天真,就用除法就完事了!!但是,,注意溢出。。
int divide(int dividend, int divisor)
//溢出判断
if(dividend == -2147483648 && divisor == -1) return 2147483647;
return dividend/divisor;
解题思路2
首先处理溢出的情况,和一些特殊情况。然后中间利用乘法的快速加实现来做判断。建议以后再看,过于难了
int MIN_INT = -2147483648; //int的最小值
int MAX_INT = 2147483647;
bool quickadd(int y, int z, int x) //判断z*y >= x?
int result = 0,add = y;
while(z)
if(z & 1)
if(result < x - add) return false;//保证 result + add >= x
result += add;
if(z != 1)
if(add < x - add) return false; // 保证add + add >= x
add += add;
z >>= 1;
return true;
int divide(int dividend, int divisor)
//异常处理
if(dividend == MIN_INT) //被除数的溢出处理
if(divisor == -1) return -(MIN_INT + 1);//超出正整数表示范围 返回2^31-1
else if(divisor == 1) return MIN_INT; //除1直接返回相应的值
if(divisor == MIN_INT) //除数的溢出处理
if(dividend == MIN_INT) return 1; //两个想等的数字相除 返回1
else return 0; //其它情况都是返回0 的
int flag = 0;//记录正负
if(dividend > 0) dividend = -dividend,flag++;//统一处理为负数
if(divisor > 0) divisor = -divisor,flag ++; //统一处理为负数
int a = 0,b = MAX_INT,ans = 0; //定义左右点和结果
while(a <= b)
int mid = a + ((b - a) >> 1);
if(quickadd(divisor,mid,dividend))
printf("d");
ans = mid;
if(mid == MAX_INT) break;
a = mid + 1;
else b = mid -1;
return flag & 1 ? -ans :ans;
50. Pow(x, n)
题目描述
实现 pow(x, n) ,即计算 x 的 n 次幂函数(即,xn)。
解题思路1
别天真,就用pow就完事了!!
double myPow(double x, int n)
return pow(x,n);
解题思路2
是利用二分快速幂的思想。建议以后再看,过于难了
double myPow(double x, int n)
double ans = 1;
unsigned int m = n;
if(n < 0) m = -(unsigned)n,x = 1.0 /x;
while(m)
if(m&1) ans *= x;
m>>=1;
x*=x;
return ans;
69. Sqrt(x)
题目描述
给你一个非负整数 x ,计算并返回 x 的 算术平方根 。
由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
注意:不允许使用任何内置指数函数和算符,例如pow(x, 0.5)或者x ** 0.5。
解题思路1
别天真,就用sqrt就完事了!!
int mySqrt(int x)
return sqrt(x);
解题思路2
利用二分的思想,去找到一个最小的能达到mid*mid < x的值。
int mySqrt(int x)
int left = 0,right = ((unsigned)1<<16);
while(left < right)
unsigned mid = left + ((right - left) >> 1);
if(mid * mid > x) right = mid;
else if(mid * mid < x) left = mid + 1;
else return mid;
return left - 1;
面试题 16.07. 最大数值
题目描述
编写一个方法,找出两个数字a和b中最大的那一个。不得使用if-else或其他比较运算符。
解题思路1
别天真,就用fmax就完事了!!
int maximum(int a, int b)
return fmax(a,b);
解题思路2
利用加减法判断正负号。为了防止溢出采用long long,然后右移可以移动符号位,移动63位就刚好可以移动变为0或者-1。然后+1就可以变为1和0。然后变成a和b就好了。
int maximum(int a, int b)
long long c = (long long) a - (long long)b;
c >>= 63;
c += 1;
return a*c + b*(!c);
📑写在最后
今天完成了第一天的打卡,最近的c语言和算法的打卡暂停了,好空虚,所以明天开一个算法笔记,希望大家可以跟我一起。0.0
以上是关于解题报告《LeetCode零基础指南》(第二讲) 函数的主要内容,如果未能解决你的问题,请参考以下文章