LeetCode回溯 JS经典题型（全排列子集与组合）汇总

Posted 2022-01-02 YuLong~W

文章目录

• 46. 全排列
• 47. 全排列 II
• 78. 子集
• 77. 组合

回溯算法： 实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就 “回溯” 返回，尝试别的路径。

回溯算法的基本思想是：从一条路往前走，能进则进，不能进则退回来，换一条路再试。 ——LeetCode

46. 全排列

原题链接：46. 全排列

/**
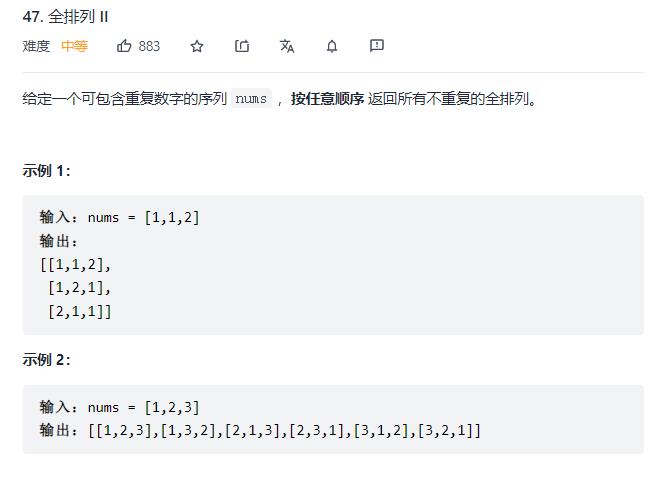
 * @param number[] nums
 * @return number[][]
 */
var permute = function(nums) 
    const res = [];
    // 用于标记使用过的值 避免重复使用同一个数字
    const used = ;

    function dfs(path) 
        if (path.length == nums.length)  // 个数选够了
            res.push(path.slice()); // 拷贝一份path，加入解集res
            return;                 // 结束当前递归分支
        
        for (const num of nums)  // for枚举出每个可选的选项
            // if (path.includes(num)) continue; // 这么写会增加时间复杂度 查找是O(n)
            if (used[num]) continue; // 使用过的，跳过
            path.push(num);         // 选择当前的数，加入path
            used[num] = true;       // 记录一下 使用了
            dfs(path);              // 基于选了当前的数，递归
            path.pop();             // 上一句的递归结束，回溯，将最后选的数pop出来
            used[num] = false;      // 撤销这个记录
        

        // 同理，也可以用for循环来写
        // for(let i=0;i<nums.length;i++)
        //     if(!used[i])
        //         used[i]=true;
        //         path.push(nums[i]);
        //         dfs(path);
        //         path.pop();
        //         used[i]=false;
        //     
        // 
      
    

    dfs([]); // 递归的入口，空path传进去
    return res;
;

注意：

• Map 结构 used的使用：填坑时，每用到一个数字，都要给这个数字打上“已用过”的标——避免它被使用第二次；数字让出坑位时，对应的排列和 used 状态也需要被及时地更新掉。

• 当走到递归边界时，一个完整的排列也完成了。将这个完整排列推入结果数组时，用了res.push(path.slice())，而不是简单的res.push(path) 。因为全局只有一个唯一的 path ， path 的值会随着 dfs 的进行而不断被更新。 slice方法的作用是拷贝出一个不影响path正本的副本，以防直接修改到path的引用。

47. 全排列 II

原图链接：47. 全排列 II

对数组进行排序，并且边界条件进行前后重复比对，其余解题步骤与上题一致

/**
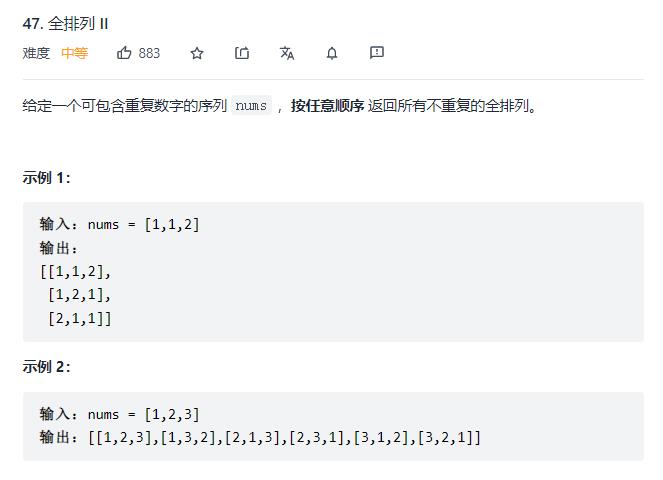
 * @param number[] nums
 * @return number[][]
 */
var permuteUnique = function(nums) 
	//先对数组进行排序
    nums.sort((a,b)=>a-b);

    const res=[];
    const used=;

    function dfs(path)
        if(path.length===nums.length)
            res.push(path.slice());
            return;
        
        for(let i=0;i<nums.length;i++)
            // 每次填入的数一定是这个数所在重复数集合中 从左往右第一个未被填过的数字
            if(i>0 && nums[i]===nums[i-1] && !used[i-1]) continue;
            if(!used[i])
                used[i]=true;
                path.push(nums[i]);
                dfs(path);
                path.pop();
                used[i]=false;
            
        
    
    dfs([]);
    return res;
;

78. 子集

原题链接： 78. 子集

/**
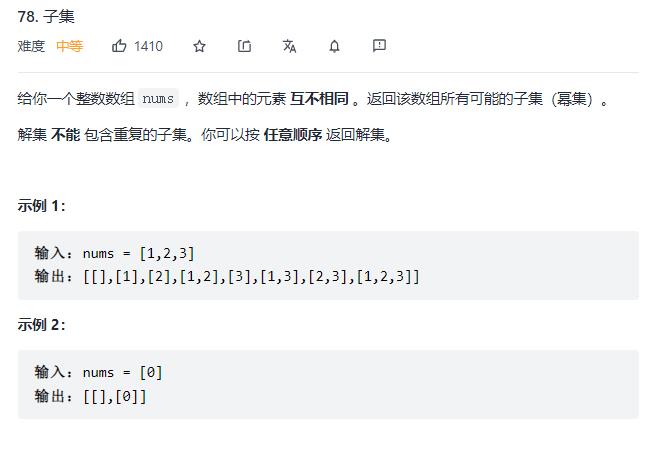
 * @param number[] nums
 * @return number[][]
 */
var subsets = function(nums) 
    // 结果数组
    const res=[];
    // 组合数组
    const subset=[];
    const len=nums.length;
    // 进入dfs
    dfs(0);

    function dfs(index)
        // 每次进入，组合更新一次，推入结果数组
        res.push(subset.slice());
        for(let i=index;i<len;i++)
            subset.push(nums[i]);
            // 基于当前数字存在于组合中 进一步dfs
            dfs(i+1)
            // 当前数字不存在组合情况
            subset.pop();
        
    
    return res;
;

77. 组合

原题链接： 77. 组合

/**
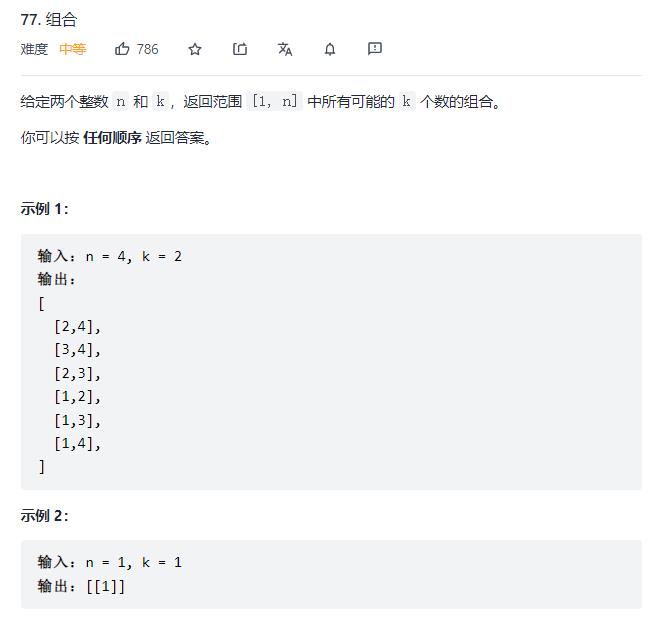
 * @param number n
 * @param number k
 * @return number[][]
 */
var combine = function(n, k) 
    // 参数不是nums数组 而是数字范围边界n
    const res=[];
    const subset=[];
    // 起始从1开始
    dfs(1);

    function dfs(index)
        if(subset.length===k)
            res.push(subset.slice());
            return;
        
        // 遍历inde——n之间所有数字
        for(let i=index;i<=n;i++)
            subset.push(i);
            dfs(i+1);
            subset.pop();
        
    
    return res;
;

总结：

1、什么时候用：

看两个特征：

• 题目中暗示了一个或多个解，并且要求我们详尽地列举出每一个解的内容时，一定要想到 DFS、想到递归回溯。
• 题目经分析后，可以转化为树形逻辑模型求解。

2、为什么这样用：

递归与回溯的过程，本身就是穷举的过程。题目中要求我们列举每一个解的内容，解从哪来？解是基于穷举思想、对搜索树进行恰当地剪枝后得来的。

注意到另一种问法：不问解的内容，只问解的个数。这类问题往往不用 DFS 来解，而是用动态规划

3、怎么用：

一个模型——树形逻辑模型；两个要点——递归式和递归边界。

• 树形逻辑模型的构建，关键在于找“坑位”，一个坑位就对应树中的一层，每一层的处理逻辑往往是一样的，这个逻辑就是递归式的内容。
• 递归边界，要么在题目中约束得非常清楚、要么默认为“坑位”数量的边界。

用伪代码总结一下编码形式，大部分的题解都符合以下特征：

function xxx(入参) 
  前期的变量定义、缓存等准备工作 
  
  // 定义路径栈
  const path = []
  
  // 进入 dfs
  dfs(起点) 
  
  // 定义 dfs
  dfs(递归参数) 
    if(到达了递归边界) 
      结合题意处理边界逻辑，往往和 path 内容有关
      return   
    
    
    // 注意这里也可能不是 for，视题意决定
    for(遍历坑位的可选值) 
      path.push(当前选中值)
      处理坑位本身的相关逻辑
      path.pop()