AI Studio 对于波士顿房价的线性回归

Posted 2022-01-02 卓晴

简 介： 这是利用线性回归模型来 处理波士顿房价的预测。通过随机梯度下降完成模型的训练。对于最终的结果来看，预测的误差还是非常大的。

关键词： 波士顿房价，NN，AI

 

§01 创建项目

---

一、创建带有housing.data的项目

  进入AI Studio用户的主页，打开“项目”中的“创建和Fork项目”，点击“创建”，进行项目的创建。

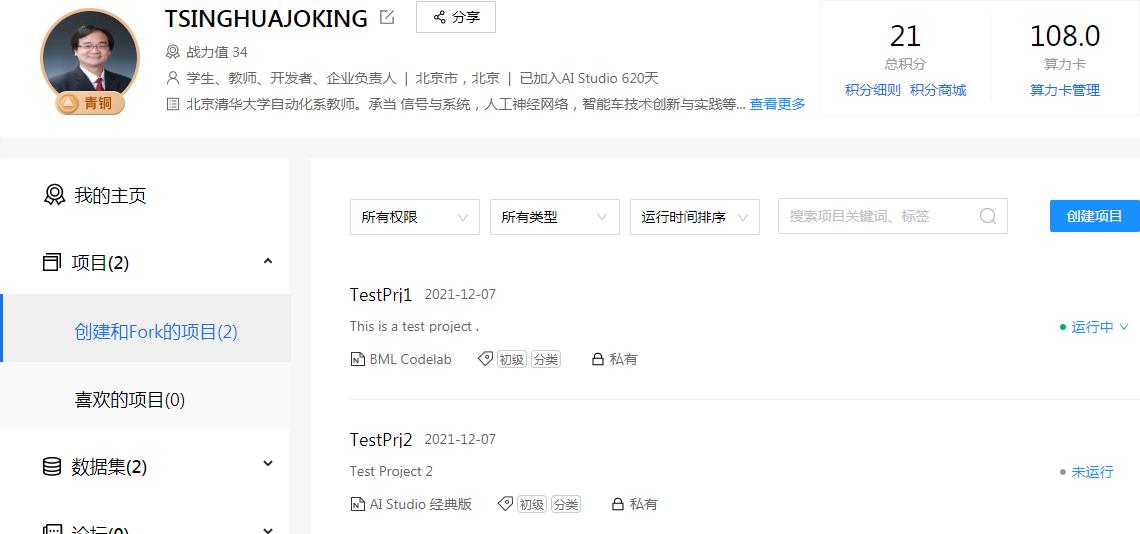
▲ 图1.1.1 AI Studio下的项目管理界面

  选择创先Notebook类型的项目，可以加快交互过程。

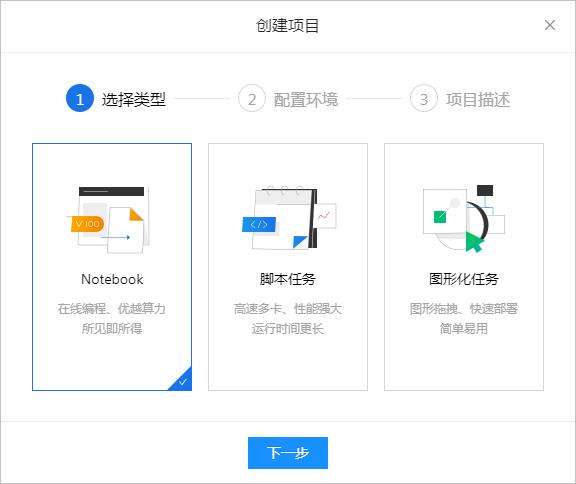
▲ 图1.1.2 选择Notebook类型的项目

  在配置环境中选择BML CodeLab。 对于项目框架选择：PaddlePaddle 2.2.0, 项目环境选择 Python3.7。

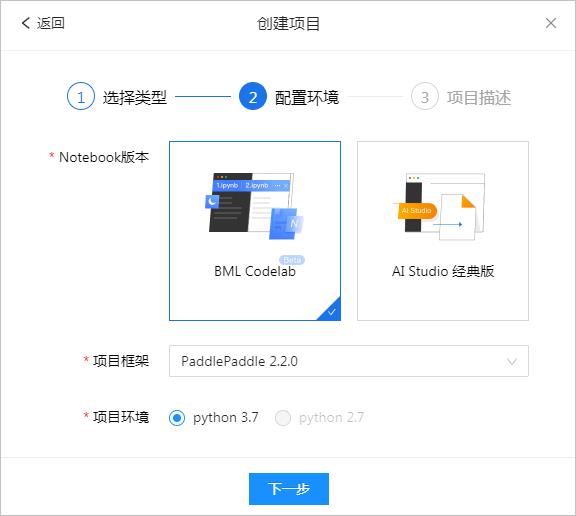
▲ 图1.1.4 选择BML CodeLab进行配置环境

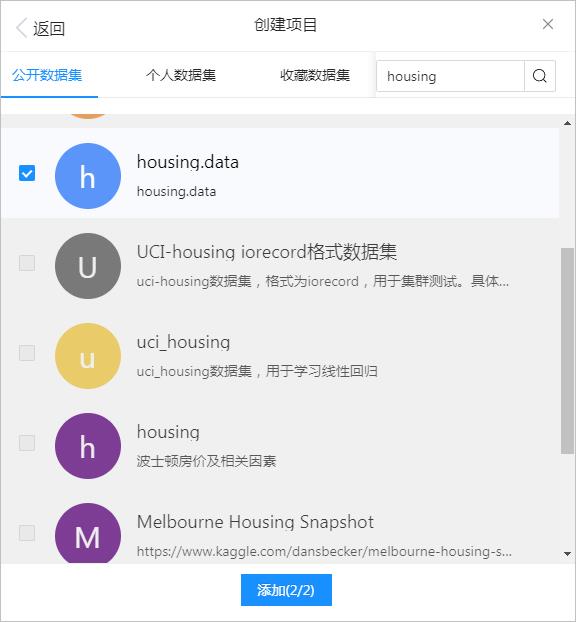
▲ 图1.1.3 选择波士顿房价数据集合

  然后最终在建立的项目中，存在data目录中，就自动带有housing.data。

1、housing.data结构

  下面是housing.data前几行的内容。

 0.00632  18.00   2.310  0  0.5380  6.5750  65.20  4.0900   1  296.0  15.30 396.90   4.98  24.00
 0.02731   0.00   7.070  0  0.4690  6.4210  78.90  4.9671   2  242.0  17.80 396.90   9.14  21.60
 0.02729   0.00   7.070  0  0.4690  7.1850  61.10  4.9671   2  242.0  17.80 392.83   4.03  34.70
 0.03237   0.00   2.180  0  0.4580  6.9980  45.80  6.0622   3  222.0  18.70 394.63   2.94  33.40
 0.06905   0.00   2.180  0  0.4580  7.1470  54.20  6.0622   3  222.0  18.70 396.90   5.33  36.20
 0.02985   0.00   2.180  0  0.4580  6.4300  58.70  6.0622   3  222.0  18.70 394.12   5.21  28.70
 0.08829  12.50   7.870  0  0.5240  6.0120  66.60  5.5605   5  311.0  15.20 395.60  12.43  22.90
 0.14455  12.50   7.870  0  0.5240  6.1720  96.10  5.9505   5  311.0  15.20 396.90  19.15  27.10
 0.21124  12.50   7.870  0  0.5240  5.6310 100.00  6.0821   5  311.0  15.20 386.63  29.93  16.50
 0.17004  12.50   7.870  0  0.5240  6.0040  85.90  6.5921   5  311.0  15.20 386.71  17.10  18.90
 0.22489  12.50   7.870  0  0.5240  6.3770  94.30  6.3467   5  311.0  15.20 392.52  20.45  15.00
 0.11747  12.50   7.870  0  0.5240  6.0090  82.90  6.2267   5  311.0  15.20 396.90  13.27  18.90
 0.09378  12.50   7.870  0  0.5240  5.8890  39.00  5.4509   5  311.0  15.20 390.50  15.71  21.70

▲ 图1.1.5 数据各段的含义

2、预测模型

线性预测模型来描述影响放假和各种影响因素之间的关系。

$$y=\sum _{j=1}^M{x}_j{w}_j+b$$

其中：

wj：模型权重
b：偏置

$$MSE=\frac{1}{n}\sum _{i=1}^n{\left({\hat{Y}}_i-Y_i\right)}^2$$

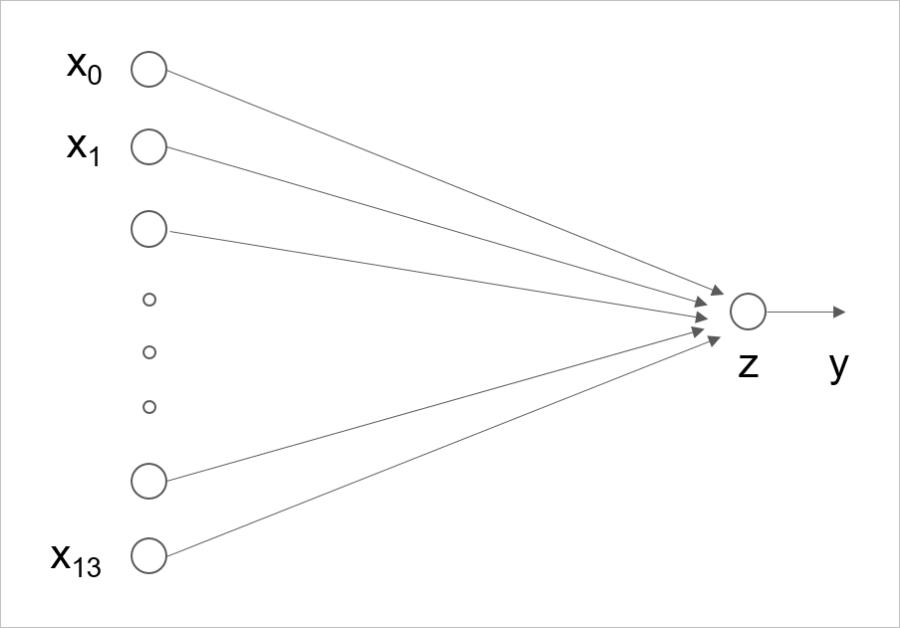
▲ 图1.1.6 线性回归单个神经网络模型

二、读取数据库

1、读取数据

（1）数据调入data

  利用numpy 读取数据。

data = fromfile(datafile, sep=' ')
printf(data)
printf(len(data))

  可以看到读取的数据为一列数据。

[6.320e-03 1.800e+01 2.310e+00 ... 3.969e+02 7.880e+00 1.190e+01]
7084

（2）数据转换成二维矩阵

feature_names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS',
                 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTA', 'MEDV']

feature_num = len(feature_names)

data = data.reshape([data.shape[0]//feature_num, feature_num])
printf(data)

#------------------------------------------------------------
data_file = 'data/data58711/housing.data'

feature_names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS',
                     'RAD', 'TAX', 'PTRATIO', 'B', 'LSTA', 'MEDV']

def load_file(filename, ratio):
    data = fromfile(filename, sep = ' ')

    feature_num = len(feature_names)
    data = data.reshape([data.shape[0]//feature_num, feature_num])

    train_num = int(data.shape[0]*ratio)
    train_data = data[:train_num]

    maximums, minimums, averages = (train_data.max(axis=0),
                                    train_data.min(axis=0),
                                    train_data.sum(axis=0)/train_data.shape[0])

    for i in range(feature_num):
        data[:,i] = (data[:,i] - minimums[i]) / (maximums[i] - minimums[i])

    train_data = data[:train_num]
    test_data = data[train_num:]
    return train_data, test_data

#------------------------------------------------------------
training_data, testing_data = load_file(data_file, 0.8)
x = training_data[:,:-1]
y = training_data[:,-1:]

2、数据预处理

（1）分割训练与测试集合

train_data_ratio = 0.8
train_data_offset = int(data.shape[0]*train_data_ratio)
train_data = data[:train_data_offset]

（2）数据归一化

maximum, minimum, averages = (train_data.max(axis=0),
                              train_data.min(axis=0),
                              train_data.sum(axis=0)/train_data.shape[0])
printf(maximum, minimum, averages)

[ 88.9762 100.      25.65     1.       0.871    8.78   100.      12.1265
  24.     666.      22.     396.9     37.97    50.    ] [6.3200e-03 0.0000e+00 4.6000e-01 0.0000e+00 3.8500e-01 3.5610e+00
 2.9000e+00 1.1296e+00 1.0000e+00 1.8700e+02 1.2600e+01 7.0800e+01
 1.7300e+00 5.0000e+00] [1.91589931e+00 1.42326733e+01 9.50232673e+00 8.66336634e-02
 5.31731931e-01 6.33310891e+00 6.44274752e+01 4.17421361e+00
 6.78960396e+00 3.52910891e+02 1.80262376e+01 3.79971757e+02
 1.13549505e+01 2.41757426e+01]

（3）绘制数据曲线

def plotx_y(x, y, features=''):
    xy = sorted(zip(x.flatten(),y.flatten()), key=lambda x:x[0])
    x = [s[0] for s in xy]
    y = [s[1] for s in xy]

    plt.plot(x,y)
    plt.xlabel(features)
    plt.ylabel(feature_names[-1])
    plt.title(features)
    plt.grid(True)
    plt.tight_layout()
#    plt.savefig('plot.png')
    plt.show()

#------------------------------------------------------------
id = 11
plotx_y(x[:,id], y, feature_names[id])

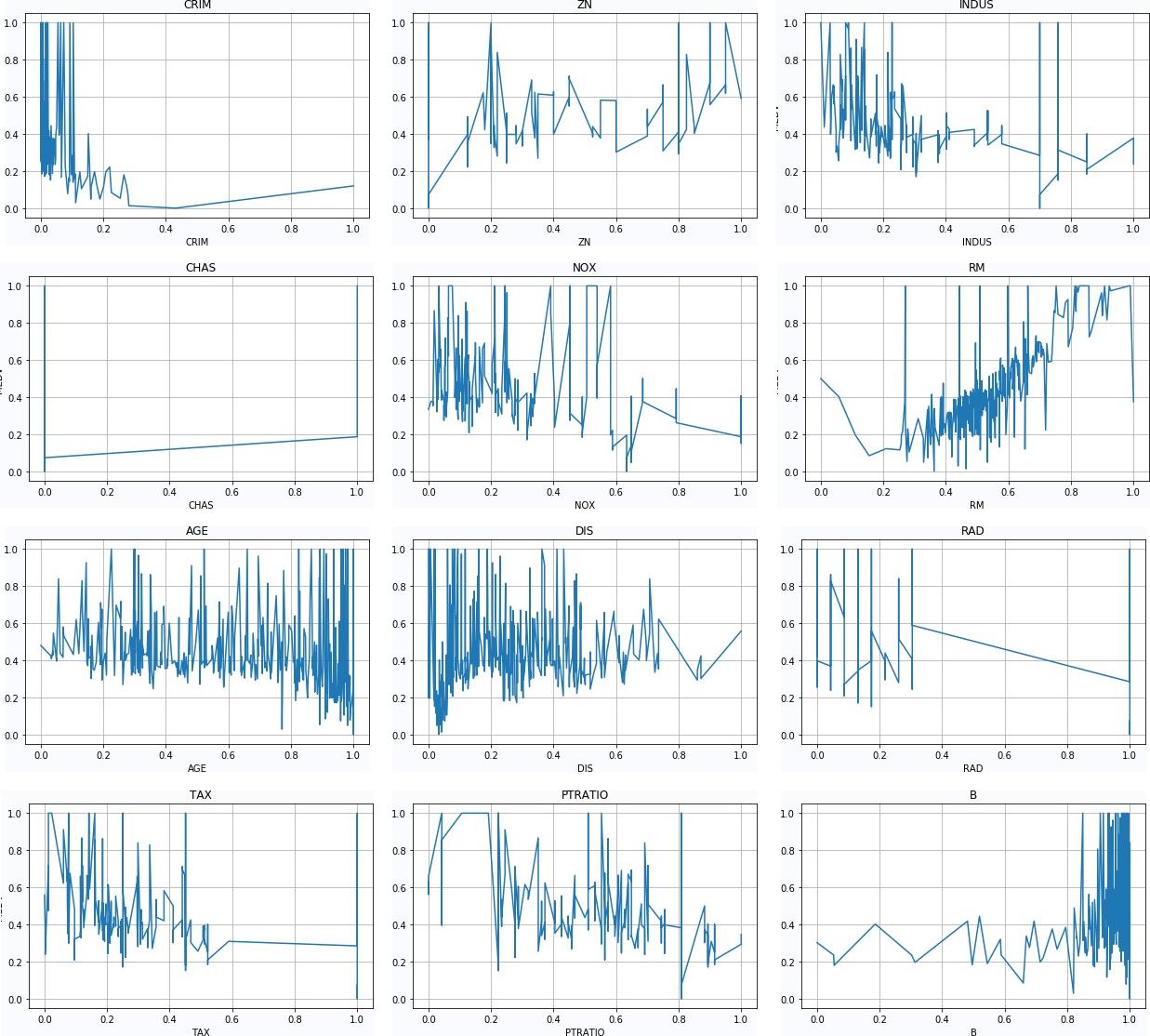
▲ 图1.2.1 数据曲线

3、模型设计

  设计Network的类，来计算对应的 预测输出。

（1）网络设计

class Network(object):
    def __init__(self, num_of_weights):
        random.seed(0)
        self.w = random.randn(num_of_weights, 1)
        self.b = 0

    def forward(self, x):
        z = dot(x, self线性回归模型之波士顿房价预测

 线性回归案例：波士顿房价预测
 机器学习之利用线性回归预测波士顿房价和可视化分析影响房价因素实战（python实现 附源码 超详细）
 机器学习实战—— 用线性回归预测波士顿房价
 《用Python玩转数据》项目—线性回归分析入门之波士顿房价预测
 机器学习之路: python 线性回归LinearRegression, 随机参数回归SGDRegressor 预测波士顿房价