概率统计笔记： 协方差与相关系数

Posted 2022-01-02 UQI-LIUWJ

1 协方差

1.1 定义

假设两个随机变量X和Y满足未知的概率分布，那么X和Y的协方差为：

其中E是求解数学期望的运算符，μx，μy分别是X和Y的均值

1.2 存在的问题

        协方差告诉我们两个随机变量是如何一起移动的，但只用协方差衡量变量相关性存在一些问题：协方差是有量纲的，它的大小受随机变量本身取值范围的影响。

2 相关系数

        人们希望使用某个和协方差有关，但是又是无量纲的测量来描述两个随机变量的相关性。

        最简单的做法就是用变量自身的波动对协方差进行标准化，相关系数便由此得来。

2.1 相关系数的定义

        令ρ表示X和Y的相关系数，它的定义为

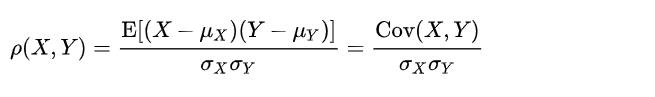
        其中σx和σy分别是X和Y的标准差

        通过使用X和Y的标准差对它们的协方差归一化，ρ的取值范围为 [-1, +1]： 

2.2 相关系数和XY分布之间的关系

• ρ(X,Y)=1表示X和Y之间存在确切的线性正相关；

• ρ(X,Y)=0表示X和Y之间不存在任何线性相关性；

• ρ(X,Y)=-1表示X和Y之间存在确切的线性负相关。

        值得一提的是，相关系数仅仅刻画 X和Y之间的线性相关性；它不描述它们之间的（任何）非线性关系。

3 时间序列的自相关系数

3.1 时间序列的弱平稳性

算法笔记：ARIMA_UQI-LIUWJ的博客-CSDN博客 提及了弱平稳性

我们这里涉及的弱平稳性性质是：如果时间序列数据具有弱平稳性，那么对于所有的时刻t和任意的间隔k，值之间的协方差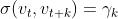,其中γk与时间t无关。他仅仅依赖于时间间隔k。

（比如样本是 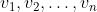,那么)

3.2 自相关系数ACF

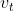和的自相关系数称为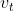的间隔为k的自相关系数。

 当k=0的时候，有：

说明对任何时刻t， 的间隔为k的自相关系数恒为1 

 进一步，我们计算

 

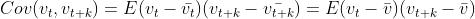
【弱平稳性的性质，时间序列的期望不变】

这里的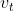是 ,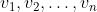

 所以 

【注：也有很多版本底下除的是n，就不太明白究竟应该是哪个。。。但如果n很大h很小的时候，差距并不是很大】

3.2.1 自相关图解读

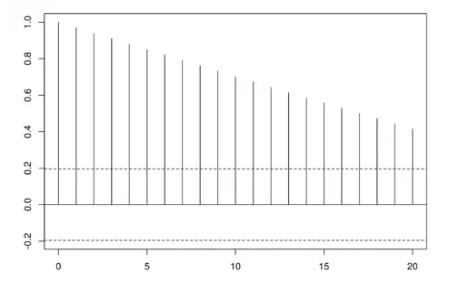
下面为一些时间序列的自相关图。它们呈现出完全不同结构的自相关性。

 

这个自相关图的时间序列存在明显的趋势

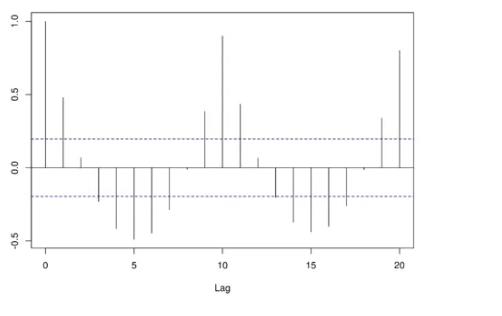
这个相关图的时间序列存在明显的周期性。

 

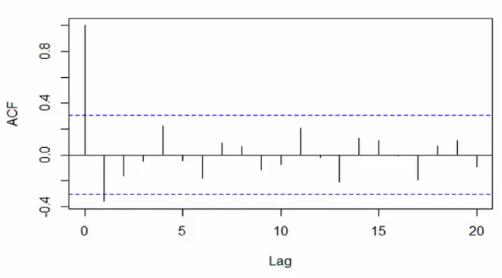
 这个则同时有一定的趋势和周期性