概率统计笔记：白噪声与随机游走

Posted 2022-01-02 UQI-LIUWJ

1 白噪声

1.1 定义

        白噪声是一个理想中的时序模型，它有一个重要的特性，即序列不相关：一个白噪声序列中的每一个点都独立的来自某个未知的分布，即它们满足独立同分布。

        考虑时间序列 。如果该序列的成分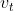 满足均值为0方差为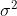,且对于任意大于等于1的k， 自相关系数均为0，则称该时间序列为一个白噪声。

        

 1.2 作用

        一个优秀的时序模型拟合出的残差序列应该（近似）为一个白噪声。（残差序列：拟合值-观测值。

        使用白噪声序列的性质可以帮助我们确认我们的残差序列中没有任何相关性了，一旦残差序列没有相关性便意味着模型是原始时间序列的一个良好的拟合。

2 随机游走

2.1 定义

        对于时间序列 xt，如果它满足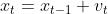,其中vt是一个均值为0方差为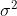的白噪声，那么序列 xt 为一个随机游走。 (x0=v0)

        由定义我们可以知道，任何时刻的xt，都可以表示为不超过t时刻的所有历史白噪声序列的总和

 

2.1 随机游走的均值和方差

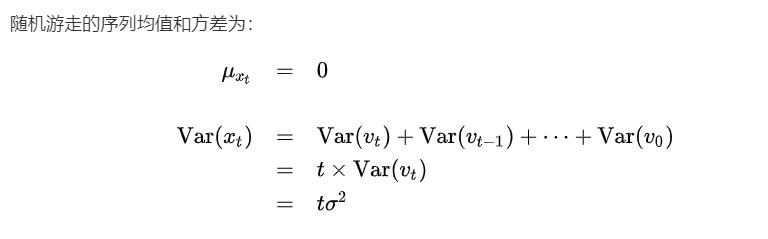
由于方差是一个σ的函数，所以不满足弱稳定性的定义【至少时间间隔k=0的协方差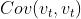就不是 一个和t无关的函数】 

随着t的增加，方差增大，说明随机游走的波动性会不断增加。

参考内容：【TS技术课堂】时间序列统计分析