A Exam：Machine Learning with Python

Posted 2022-01-02 amcomputer

机器学习题目，目前已经做好了，1-7，9共八道题目。共99RMB, 需要的私聊。

Problem 1 [8 pts]

You are robot in a lumber yard, and must learn to discriminate Oak wood from Pine wood. You
choose to learn a Decision Tree Classifier. You are given the following examples:

(a) [3 pts] Calculate the information gain for each attribute for (1). Which attribute is the best for
(1)? Fill in ① and ②.

(b) [3 pts] Calculate the information gain for each attribute for (2). Which attribute is the best for
(2)? Fill in ③ and ④.

© [2 pts] Classify these new examples as Oak or Pine using your decision tree above.
i. What class is [Density = Light, Grain = Small, Hardness = Hard]?
ii. What class is [Density= Light, Grain = Small, Hardness = Soft]?

Problem 2 [3 pts]

Consider the following training set in the 2-dimensional Euclidean space:


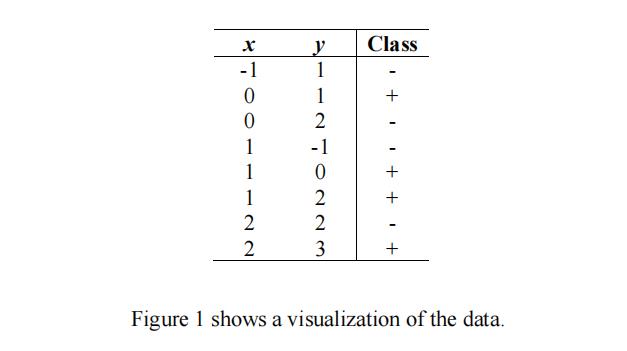
(a) [1 pt] What is the prediction of the 3-nearest-neighbor classifier at the point (1,1)?

(b) [1pt] What is the prediction of the 5-nearest-neighbor classifier at the point (1,1)?

© [1pt] What is the prediction of the 7-nearest-neighbor classifier at the point (1,1)?

Problem 3 [4 pts]

Suppose we are learning a classifier with binary output values Y = 0 and Y = 1. There are two real valued input attributes X1 and X2. Here is our data:


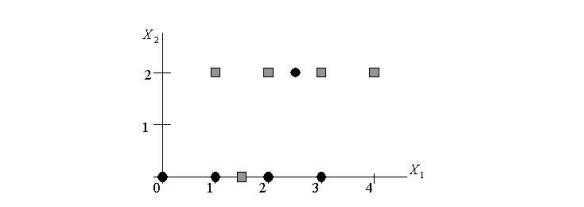
Assume we will learn a decision tree using ID3 algorithm on this data.
Assume that when the decision tree splits on the real-valued attributes, it putsthe split threshold halfway
between the values that surround the highest-scoring split location. For example, if X2 is selected as
the root attribute, the decision tree would choose to split at X2 = 1, which is halfway between X2 = 0
and X2 = 2.
Let Algorithm DT2 be the method of learning a decision tree with only two leaf nodes (i.e. only one
split), and Algorithm DT* be the method of learning a decision tree fully with no pruning.
(a) (2 pts) What will be the training set error of DT2 and DT* on our data? Express your answer
as the number of misclassifications out of 10.
DT2:
DT*:

(b) (2pts) What will be the leave-one-out cross-validation error of DT2 and DT* on our data?
DT2:
DT*:

• Leave-one-out cross validation is K-fold cross validation taken to its logical extreme, with K equal
  to N, the number of data points in the set. That means that N separate times, the function approximator
  is trained on all the data except for one point and a prediction is made for that point.

Problem 4 [3 pts]

Support vector machines learn a decision boundary leading to the largest margin from both classes.
You are training a Support Vector Machine (SVM) on a tiny dataset with 4 points shown in Figure 1

(a) [2 pts] Find w1, w2 and b from a decision boundary f(x1, x2) = w1⋅x1+w2⋅x2+b?
(b) [1 pt] Choose all support vectors (the data points that lie closest to the decision surface)

Problem 5 [6 pts]

Consider fitting the linear regression model for these data.

Assume you solve the problems using least squares.
(a) [3 pts] Fit 𝑌𝑌𝑖𝑖 = 𝛽𝛽0, find 𝛽𝛽0. Explain how you got your answer.

(b) [3 pts] Fit 𝑌𝑌𝑖𝑖 = 𝛽𝛽1𝑋𝑋𝑖𝑖, find 𝛽𝛽1. Explain how you got your answer.

Problem 6 [4 pts]

Suppose your training set for two-class classification in one dimension (d=1, 𝑥𝑥𝑖𝑖 ∈ ℝ) contains three
sample points:
point 𝑥𝑥1 = 3 with label 𝑦𝑦1 = 1,
point 𝑥𝑥2 = 1 with label 𝑦𝑦2 = 1, and
point 𝑥𝑥3 = −1 with label 𝑦𝑦3 = −1.
What are the values of w and b given by a logistic regression (with no regularization)?

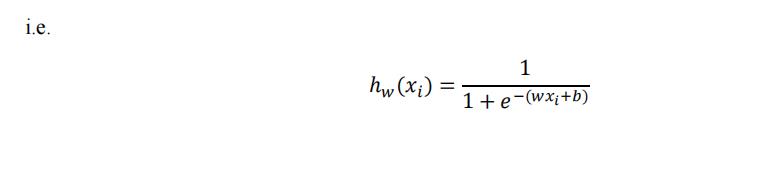
Problem 7 [9 pts]

We are interested in predicting whether a person makes over 50K a year. For simplicity suppose we
model the two features with two boolean variables 𝑋𝑋1, 𝑋𝑋2 ∈ 0,1 and label 𝑌𝑌 ∈ 0,1 where 𝑌𝑌 = 1 indicates a person makes over 50K. In Figure, we show three positive samples (“+” for 𝑌𝑌 = 1) and
one negative samples (“-” for 𝑌𝑌 = 0). Please complete the following questions.

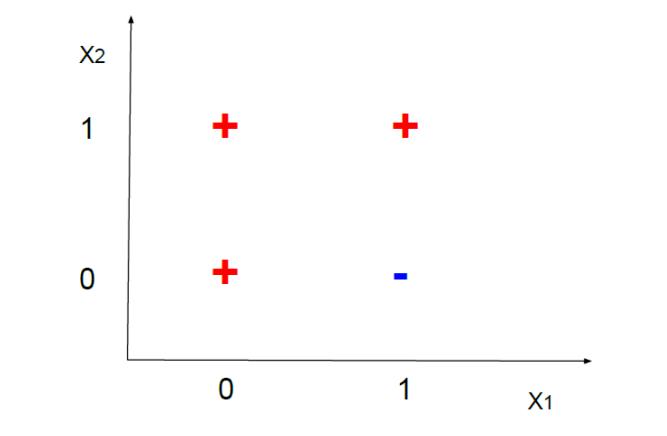
(a) [1 pts] If we train a k-NN classifier (k=3) based on data in Figure, and then try to classify the
same data. Which sample(s) must be misclassified by this classifier?

(b) [1 pts] For predicting samples in Figure, which model is better: Logistic Regression or Linear
Regression. Why?

© [1.5 pts] Is there any logistic regression classifier using X1 and X2 that can perfectly classify
the examples in Figure? Why?

(d) [1.5 pts] How about if we change label of point (0,1) from “+” to ”-”? Why?

(e) [2 pts] Suppose we have trained a linear regression model y=ax+b where a=0.5 and b=1.0, on
a set of training data points D = (1.0, 1.6), (1.5, 1.5), (3.0, 2.4). Please calculate the mean
squared errors (MSE) of this model on D (MSE = mean of error2
). Write down how you got
your answer.

(f) [2 pts] If we train a classifier based on data in Figure, and then we apply that classifier on a
testing dataset. The testing confusion matrix is given by:

What is the precision and recall of that classifier?

Problem 8 [9 pts]

Use k-means algorithm to create two clusters. The initial centroids are 𝜇1 = (2,2) and 𝜇2 = (1,1).
Measure the distance using the Euclidean distance:
e.g ) distance between 𝜇1 and 𝜇2 = (2 − 1)2 + (2 − 1)^2

1. [5 pts] Fill in the following table:
2. 
3. [2 pts] Re-compute the new centroids.
4. 
   

Problem 9 [3 pts]

Suppose you have inputs as x = −2, y = 5, and z = −4. You have a neuron q and neuron f with functions:
q = x + y
f = q ∗ z
What is the gradient of f with respect to x, y, and z? See the figure below:

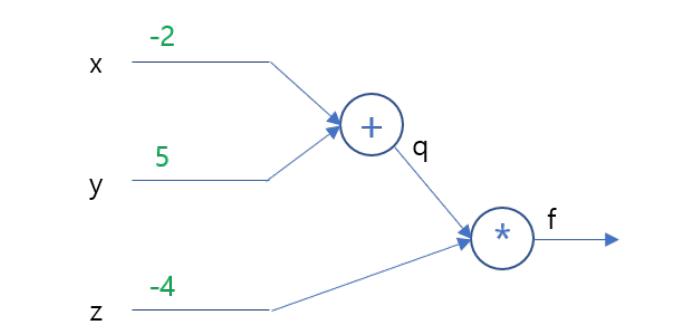
Problem 10 [3 pts]

Consider the following convolution procedure:
Greyscale Image --> Convolution with filter A (no padding, stride=1) --> 2x2 maxpool --> Output
A =

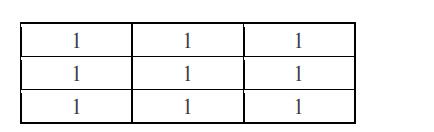
When the input image is

what is the output of the convolution procedure?

Problem 11 [2 pts]

Suppose you are learning a CNN on grayscale images of size 105x154, so the image has only one
channel. In the first convolutional layer, you use a filter of size 21x14 with stride of size 7 in both x and
y dimensions without any padding or bias term. How many neurons will there be in the next layer?

Problem 12 [2 pts]

After performing SVD on a dataset with 5 features, you retrieve eigenvalues 6, 5, 4, 3, 2. How many
components should we include to explain at least 75% of the variance of the dataset?
(Hint: we choose k explaining 99% of the variance PCA)

Problem 13 [4 pts]

Consider a recommender system using collaborative filtering. The movie rating matrix is as follows:

(1) [2 pts] Predict (Movie1, Movie3, Movie4) ratings of User A.

(2) [2 pts] Predict (Movie1, Movie2, Movie3, Movie4) ratings of a new User E using mean
normalization.