POSEIDON: A New Hash Function for Zero-Knowledge Proof Systems 学习笔记

Posted 2022-01-02 mutourend

1. 引言

Grassi等人2019年论文《POSEIDON: A New Hash Function for Zero-Knowledge Proof Systems》。

前序博客有：

• snark/stark-friendly hash函数
• HADES Strategy

相关代码实现有：

• https://github.com/dusk-network/Poseidon252
• https://github.com/shamatar/poseidon_hash
• https://github.com/daira/pasta-hadeshash
• https://github.com/zcash/orchard/blob/main/src/circuit/gadget/poseidon.rs
• https://github.com/lovesh/bulletproofs-r1cs-gadgets/blob/master/src/gadget_poseidon.rs
• https://github.com/shamatar/rescue_hash（Rescue hash）

SNARK、STARK、Bulletproofs（PLONK/RedShift）中，若用于proof of knowledge of a preimage under a certain cryptographic hash function时，都需要消耗大量的计算。

所谓proof of knowledge of a preimage under a certain cryptographic hash function，针对的场景为：

• public info：$h,H$
• private info：$x$
• 待证明relation：$h=H(x)$

其中$H(\ast )$ 为hash函数。

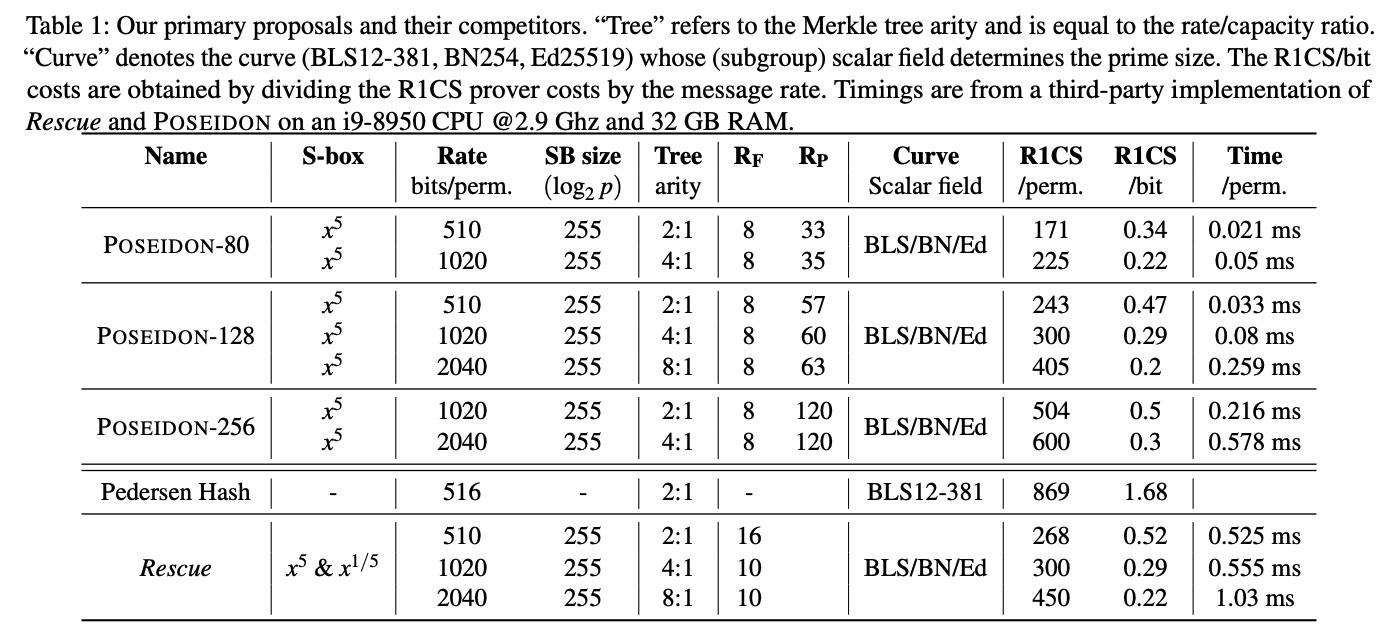
若hash函数为POSEIDON，其具有8x fewer constraints per message bit than Pedersen Hash。

POSEIDON hash可：

• 紧凑地以circuit表示
• tailored for various proof systems using specially crafted polynomials，从而进一步提升性能。

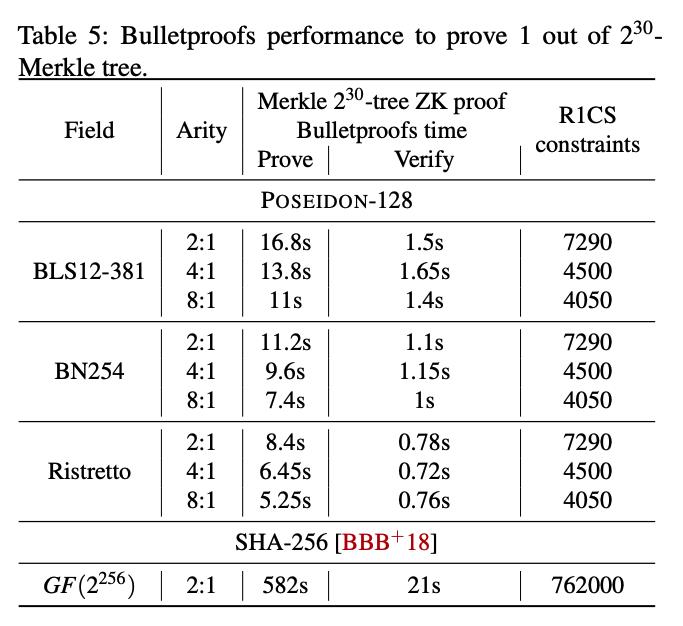
借助POSEIDON hash，采用Bulletproofs方案来实现1-out-of-10亿 membership proof with Merkle trees，所需的时间少于1秒。

1.1 不同circuit对比

此处主要考虑2种circuit：

• R1CS（rank-1 quadratic constraints）：用于ZK-SNARKs和Bulletproofs中。
• algebraic execution trace (AET) ：用于ZK-STARKs和PLONK中。

1）R1CS（rank-1 quadratic constraints）：
Bulletproofs 和 ZK-SNARKs 采用R1CS format（rank-1 quadratic constraints）来描述circuit，表示为一组二次多项式：
$L_1(X)\cdot L_2(X)=L_3(X)$
其中$X$为the tuple of internal and input variables，$L_i$为affine forms，$\cdot$为the field multiplication。
R1CS circuit中的加法门和乘法门都是定义在prime field $GF(p)$内。$GF(p)$为the scalar field of an elliptic curve，对应ZK-SNARKs来说，该椭圆曲线通常需pairing-friendly；对于Bulletproofs来说，该椭圆曲线通常仅需为secure curve即可。
R1CS的proof generation complexity与constraints的数量$T$成正比，而constraints的数量$T$通常与乘法门的数量相关。

2）algebraic execution trace (AET)：
algebraic execution trace (AET) 将computation 表示为 a set of internal program states related to each other by polynomial equations of degree $d$。该state包含了$w$ field elements，并经历$T$ transformations。
AET的proof generation与$w\cdot d\cdot T$ 成比例。The number and sparsity of polynomial constraints do not play a major role。

1.2 实现的POSEIDON家族

POSEIDON采用 HADES 设计策略，基于具有$t$ cells的substitution-permutation networks，使用了名为partial的rounds，采用了non-linear functions only for part of the state。
POSEIDON中在partial rounds中仅使用了1个S-box，但是在所有其它rounds中使用了full non-linear layers（即$t$个S-box），从而可降低R1CS或AET的开销。

POSEIDON支持80、128、256-bit security：

1.3 POSEIDON性能

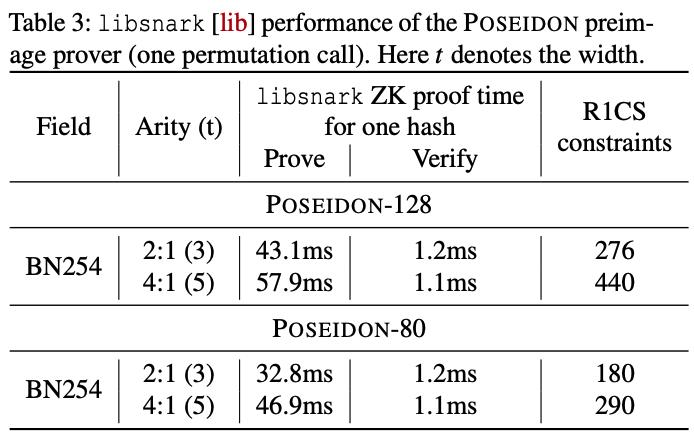
• Groth16：
  

• R1CS 用于Prove a leaf knowledge in the Merkle tree of $2^{30}$ elements：
  

• Bulletproofs 用于Prove a leaf knowledge in the Merkle tree of $2^{30}$ elements：
  

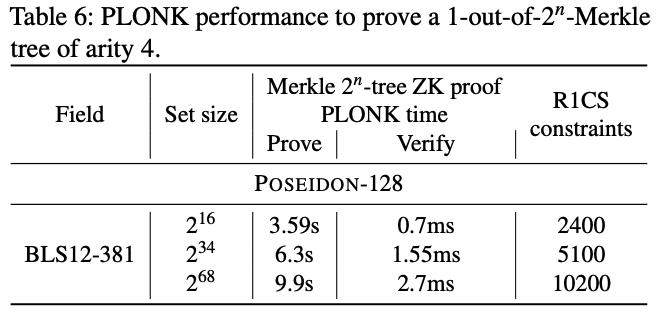
• PLONK 用于证明1-out-of-$2^n$ Merkle tree of arity of $4$：
  

2. Sponge Construction for POSEIDON

Sponge构建与Hades permutation之上，可用于实现：

• encryptiong
• authentication
• hashing

Sponge额外定义了2个参数：

• $r$：为rate。在tree hashing上下文中是指arity。rate定义了吞吐量。
• $c$：capacity。或inner part。capacity则决定了security level。

当将内部的Hades permutation size固定为$N$ bits，则需要在吞吐量和安全性之间做平衡。

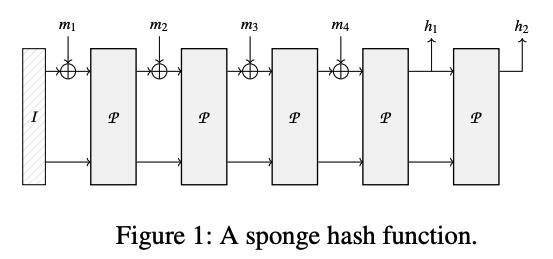
以下图为例，用于计算the hash output为$h_1||h_2$ of the $4$-block message $m_1||m_2||m_3||m_4$，其中$m_i$和$h_i$为$r$-bit values。初始state $I$为全0，即$I=0^r||0^c$ for an $r$-bit rate and a $c$-bit capacity。

3. POSEIDON hash代码解析

详细参看：

• https://github.com/dusk-network/Poseidon252/blob/master/src/sponge/sponge.rs

其中messages.chunks(WIDTH - 1) 对应为$m_1,m_2,m_3,m_4$。
state[0]对应为capacity。

/// The `hash` function takes an arbitrary number of Scalars and returns the
/// hash, using the `Hades` ScalarStragegy.
///
/// As the paper definition, the capacity `c` is set to [`WIDTH`], and `r` is
/// set to `c - 1`.
///
/// Considering `r` is set to `c - 1`, the first bit will be the capacity and
/// will have no message addition, and the remainder bits of the permutation
/// will have the corresponding element of the chunk added.
///
/// The last permutation will append `1` to the message as a padding separator
/// value. The padding values will be zeroes. To avoid collision, the padding
/// will imply one additional permutation in case `|m|` is a multiple of `r`.
pub fn sponge_hash(messages: &[BlsScalar]) -> BlsScalar 
    let mut h = ScalarStrategy::new();
    let mut state = [BlsScalar::zero(); WIDTH];

    // If exists an `m` such as `m · (WIDTH - 1) == l`, then the last iteration
    // index should be `m - 1`.
    //
    // In other words, if `l` is a multiple of `WIDTH - 1`, then the last
    // iteration of the chunk should have an extra appended padding `1`.
    let l = messages.len();
    let m = l / (WIDTH - 1);
    let n = m * (WIDTH - 1);
    let last_iteration = if l == n 
        m.saturating_sub(1)
     else 
        l / (WIDTH - 1)
    ;

    messages
        .chunks(WIDTH - 1)
        .enumerate()
        .for_each(|(i, chunk)| 
            state[1..].iter_mut().zip(chunk.iter()).for_each(|(s, c)| 
                *s += c;
            );

            // Last chunk should have an added `1` followed by zeroes, if there
            // is room for such
            if i == last_iteration && chunk.len() < WIDTH - 1 
                state[chunk.len() + 1] += BlsScalar::one();

            // If its the last iteration and there is no available room to
            // append `1`, then there must be an extra permutation
            // for the padding
             else if i == last_iteration 
                h.perm(&mut state);

                state[1] += BlsScalar::one();
            

            h.perm(&mut state);
        );

    state[1]

参考资料

[1] Encoding and Hashing of Long Objects with Poseidon
[2] Dmitry Khovratovich 的hackmd系列中有多个关于Poseidon的笔记
[3] Plonk and Poseidon
[4] Poseidon: ZK-friendly Hashing