HADES Strategy

Posted 2022-01-02 mutourend

1. 引言

主要参考Grassi等人2019年论文《On a Generalization of Substitution-Permutation Networks: The HADES Design Strategy (Updated Version)》。

相关代码实现有：

• https://github.com/dusk-network/Hades252（Rust）

block ciphers和cryptographic permutations通常设计为：

• iterate an efficiently implementable round function many times 使得结果看起来像随机的。

通常，对同一round function迭代调用足够多次数，可确保round function中的一些对称和结构属性肯定会消失。

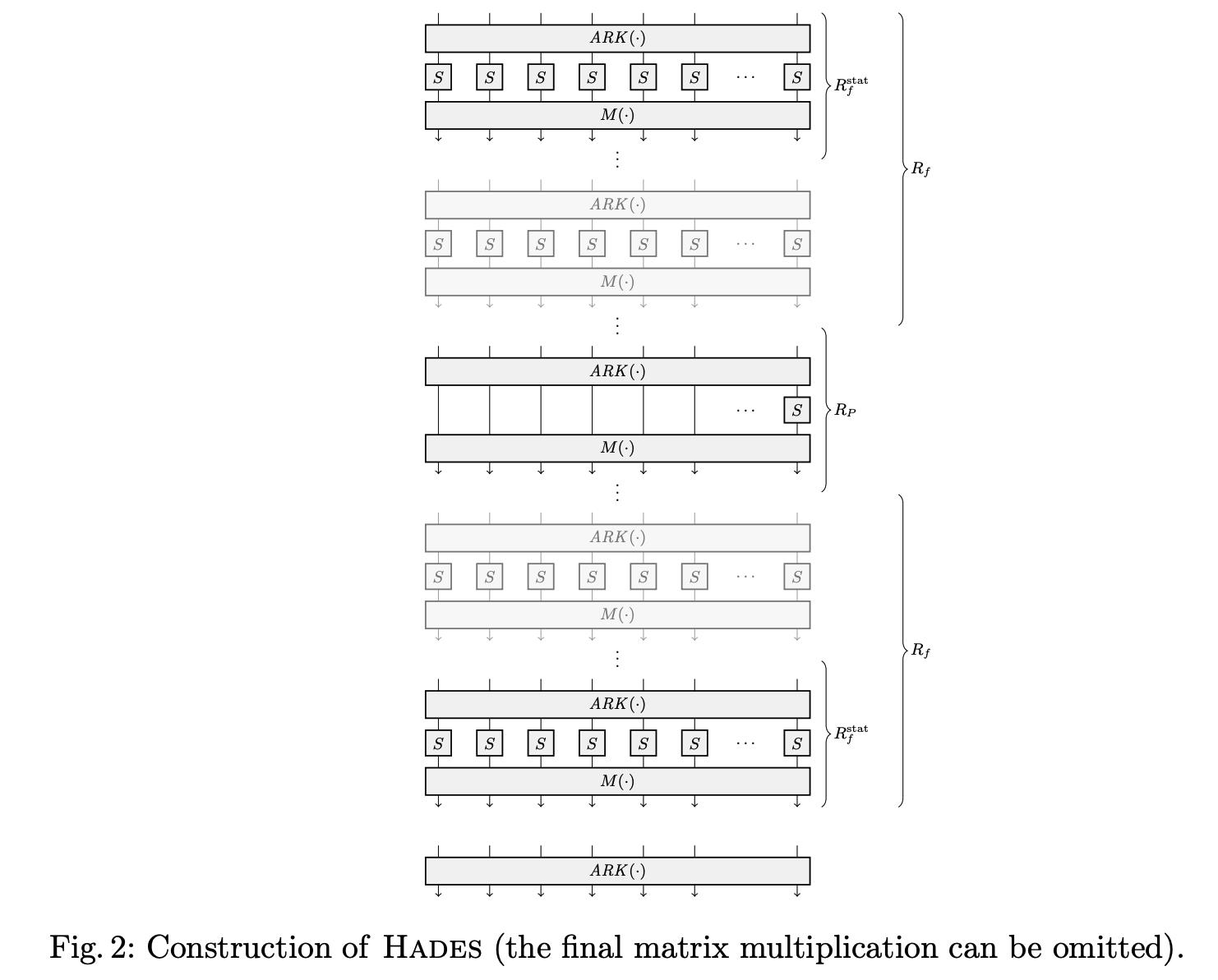
基于HADES构建的cipher，其每轮中有以下三步组成：

• 1）Add Round Key：表示为$\text{ARK}(\cdot )$
• 2）SubWords：表示为$\text{S-Box}(\cdot )$【每一轮使用的S-Box数量是不一样的。】
• 3）MixLayer：表示为$\text{M}(\cdot )$

然后，最后一轮中，MixLayer操作可忽略：

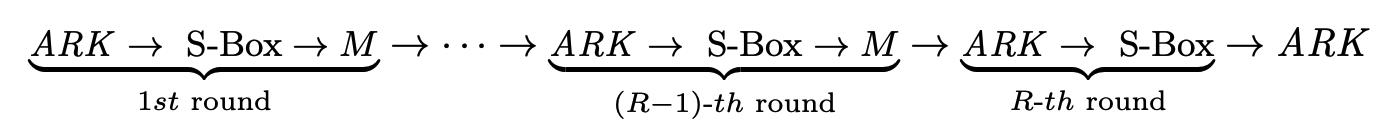
HADES中的关键特性是每一轮的S-Box数量是不一样的：

• 一定数量的轮中，标记为$R_F$，具有full S-Box layer，即$t$个S-Box functions；
• 一定数量的轮中，标记为$R_P$，具有partial S-Box layer，即$1\le s<t$个S-Box和$(t-s)$个identity functions。

接下来仅考虑$s=1$的情况。
令$R_F=2\cdot R_f$，则总的轮数为$R=2\cdot R_f+R_P$。

2. HADESMiMC

HADESMiMC中每一轮的$R_k(\cdot ):({\mathbb{F}}_p{)}^t\to ({\mathbb{F}}_p{)}^t$定义为：
$R_k(\cdot )=k+M\times \mathcal{S}(\cdot )$

其中$k\in ({\mathbb{F}}_p{)}^t$ 为secret subkey，$M\in ({\mathbb{F}}_p{)}^{t\times t}$为定义了linear layer的invertible matrix，$\mathcal{S}(\cdot ):({\mathbb{F}}_p{)}^t\to ({\mathbb{F}}_p{)}^t$为S-Box layer。
对于full S-Box layers，定义$\mathcal{S}=[S(\cdot ),\cdots ,S(\cdot )]$，对于partial S-Box layer，定义$\mathcal{S}=[S(\cdot ),I(\cdot ),\cdots ,I(\cdot )]$。其中$S(\cdot ):{\mathbb{F}}_p\to {\mathbb{F}}_p$为non-linear S-Box，$I(\cdot )$为identity function。

对于素数域$p$，non-linear S-Box定义为power map：
$\text{S-Box}(x)=x^{\alpha }$

其中$\alpha \ge 3$ 为最小整数——满足$gcd(p-1,\alpha )=1$（如当$gcd(p-1,3)=1$时$\alpha =3$，当$gcd(p-1,3)\ne 1且gcd(p-1,5)=1$时$\alpha =5$）。

3. HADESMiMC代码解析

Dusk团队实现的 https://github.com/dusk-network/Hades252（Rust）中，定义了：

• 采用BLS12-381曲线，$p=0x73eda753299d7d483339d80809a1d80553bda402fffe5bfeffffffff00000001$；
• $R_P=59,R_F=8$，每一轮最多的input width为$5$——即$t=5$；

/// Total ammount of full rounds that will be applied.
/// This is expressed as `RF` in the paper.
pub const TOTAL_FULL_ROUNDS: usize = 8;

/// Total ammount of partial rounds that will be applied.
/// This is expressed as `Rp` in the paper.
pub const PARTIAL_ROUNDS: usize = 59;

/// Maximum input width for the rounds
pub const WIDTH: usize = 5;

• Add Round Key $ARK(\cdot )$定义为在./assets/ark.bin中，总个数为960：

pub const ROUND_CONSTANTS: [BlsScalar; CONSTANTS] = 
	let bytes = include_bytes!("../assets/ark.bin");
    let mut cnst = [BlsScalar::zero(); CONSTANTS];
    ......

	fn add_round_key<'b, I>(&mut self, constants: &mut I, words: &mut [BlsScalar])
    where
        I: Iterator<Item = &'b BlsScalar>,
    
        words.iter_mut().for_each(|w| 
            *w += Self::next_c(constants);
        );
    

• $\text{S-Box}(x)=x^5$ 实现为：

fn quintic_s_box(&mut self, value: &mut BlsScalar) 
        *value = value.square().square() * *value;
    

• MixLayer $\text{M}(\cdot )$定义在./assets/mds.bin中，为$5$