LeetCodeLeetCode之打家劫舍暴力递归动态规划动态规划之优化空间的具体分析与实现

Posted 2022-01-02 Roninaxious

🔒198打家劫舍：https://leetcode-cn.com/problems/house-robber/

🎃你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

示例 1：

输入：[1,2,3,1]
输出：4
解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。

示例 2：

输入：[2,7,9,3,1]
输出：12
解释：偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。

提示：

• 1 <= nums.length <= 100
• 0 <= nums[i] <= 400

---

📕1.暴力解法-递归实现

使用递归解题首先想到的肯定是如何推导出递推公式，也就是如何分解成一个个的子问题。如果你在脑子里递来递去的，那样就陷入了一个误区，很容易思维混乱。递归最最重要的是推导出递推公式即可，至于怎么递来递去的交给计算机。

🧿（1）当nums.length=1时，那肯定最高金额就是nums[0]
🧿（2）当nums.lenght=2时，最高金额要么是nums[0]要么是nums[1]
🧿（3）当nums.length=3时，此时最高金额要么是nums[0]+nums[2]要么是nums[1]，也就是max(nums[0]+nums[2]，nums[1]);
…
🧿（4）当nums.length=n时，此时最高金额就是max(nums[n-1]，nums[n-2]+nums[n]);

你会发现当我们求nums.length=n的最大金额时相当于对上述过程进行倒推，此时递推公式就出来了。

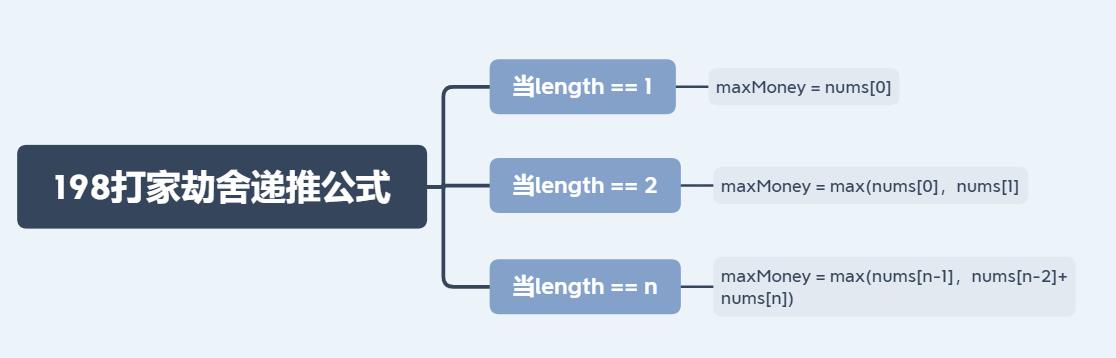
递归中第二个比较重要的是找出终止条件

🛑由于我们递推公式里包含nums[n-1]与nums[n-2]，所以为了防止数组越界，终止条件就是当n==1 || n ==2时。

代码实现：

    public static int rob(int[] nums)   
        if (nums.length == 1) //如果length=1，那么最大值肯定就是nums[0]
            return nums[0];
        
        //由于我们的终止条件是当n==0||n==1时
        //当递归从n到1时就要回溯了，此时就得考虑当n=1时，nums[1]是最大金额而不是nums[0],所以有种情况对应下面的解释
        nums[1] = Math.max(nums[0], nums[1]);
        return recursion(nums.length - 1, nums);
    

    public static int recursion(int n, int[] nums) 
        if (n == 0 || n == 1) 
            return nums[n];//这里终止条件直接返回的是nums[n],代表此时n的最大金额
            //如果n=1，那么你能否确定nums[1]是最大金额而不是nums[0]呢
            //我们在rob方法体内要进行判断，如果nums[0]>nums[1],要将nums[0]赋值给nums[1]
        
        return Math.max(recursion(n - 1, nums), recursion(n - 2, nums) + nums[n]);
    

从上图我们可以看出使用递归出现了大量的重复计算（我只是枚举前三行，越往后重复越多），这是递归比较忌讳的问题之一（重复和栈溢出）。这样无异于在浪费CPU的运算单元。

复杂度分析：
空间复杂度：O(n)【每个栈空间复杂度为O(1)】O(n*1)=O(n)
时间复杂度：O(n^n)

• 递归算法的空间复杂度与所生成的最大递归树的深度成正比。如果递归算法的每个函数调用都占用 O(m) 空间,并且如果递归树的最大深度为 n,则递归算法的空间复杂度将为 O(n·m)。”

当我使用暴力解法提交到LeetCode时，可以看出超时了，这种方式解题肯定不行。

💌上述中递归解题方式的缺点就是重复量比较多，所以我们可以可以将途中计算的结果保存下来，俗称记忆集或记忆化搜索。此时你应该想到这不正是动态规划嘛。

2.记忆化搜索-动态规划

如果你懂得了上述中的递归，那么理解动态规划解题应该比较容易，首先要根据动态规划的解题步骤进行分析

（1）分解为子问题，这个上述递归已经分析过
（2）确定状态
（3）推导转移方程，这个上述递归的递推式
（4）寻找边界条件，也就是上述递归中的终止条件

上述四个步骤，除了第二个我们都已经在上述递归中分析出来了，这个确定状态也就是用什么来保存遍历过程中的值,此题当然最适合使用一维数组进行保存
【比如dp[0]代表n=1时的最大金额；dp[1]代表n=2时的最大金额；dp[2]代表n=3时的最大金额，也就是dp[2]=max(dp[0]+nums[2],dp[1])，可以看出max中的dp[0]与dp[1]已经被记录下来了。那么一旦到dp[n]它的最大金额就可以根据前面的最优结果进行求解。】

动态规划一般都是通过迭代完成的，而不是递归。动态规划=迭代+记忆集

🎩代码实现

    public static int rob(int[] nums) 
        if (nums.length == 1) 
            return nums[0];
        
        int[] dp = new int[nums.length];//创建一个dp数组
        dp[0] = nums[0];//0和1都要先确定下来，因为下面遍历时包含i-2
        dp[1] = Math.max(nums[0], nums[1]);
        for (int i = 2; i < nums.length; i++) 
            dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);
        
        return dp[nums.length - 1];
    

复杂度分析

空间复杂度为O(n)
时间复杂度为O(n)

当我提交LeetCode上时，可以发现通过了。

分析一下：能不能将空间复杂度优化成O(1)呢？

3.动态规划之优化空间复杂度

优化成O(1)，那肯肯定就是使用0维数组作为记忆集了，经分析会发现每个结果只会被调用一次而且是有顺序性的。
比如遍历到i=4时，求maxMoney=max(nums[i-1]，nums[i-2]+nums[i])；当用完一次nums[i-1]或者nums[i-2]时后续就不会再使用

使用pre保存当n-2时的最大金额
使用suf保存当n-1时的最大金额

    public static int rob2(int[] nums) 
        if (nums.length == 1) 
            return nums[0];
        
        int pre = nums[0];
        int suf = Math.max(nums[0], nums[1]);
        int maxMoney = suf;
        for (int i = 2; i < nums.length; i++) 
            maxMoney = Math.max(pre + nums[i], suf);
            pre = suf;
            suf = maxMoney;
        
        return maxMoney;
    

复杂度分析

时间复杂度：O(n）
空间复杂度：O(1)

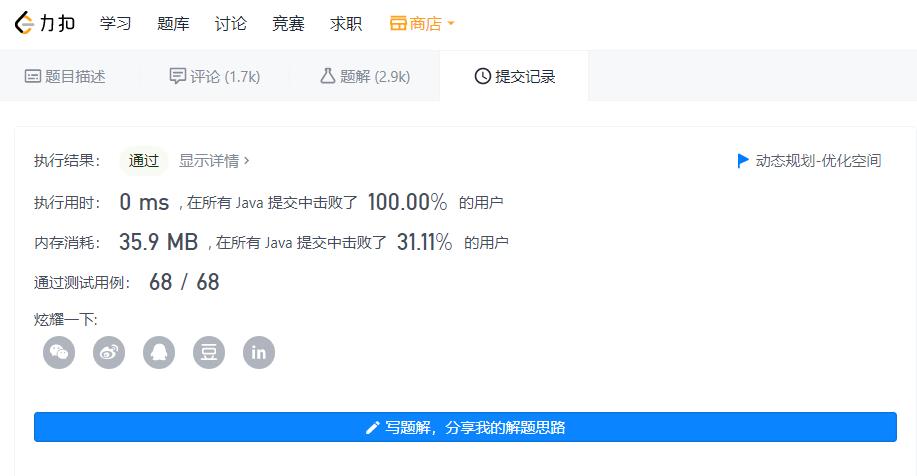
提交到LeetCode，当然能通过