LeetCodeLeetCode之打家劫舍Ⅱ——暴力递归+动态规划解决循环问题+DP空间优化

Posted 2022-01-02 Roninaxious

这道题和第 198 题相似，建议读者首先阅读「198. 打家劫舍」

🔒LeetCode之打家劫舍Ⅰ：LeetCode之打家劫舍Ⅰ

---

1.打家劫舍II 题目描述

你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警 。

给定一个代表每个房屋存放金额的非负整数数组，计算你 在不触动警报装置的情况下 ，今晚能够偷窃到的最高金额。

💎示例 1：

输入：nums = [2,3,2]
输出：3
解释：你不能先偷窃 1 号房屋（金额 = 2），然后偷窃 3 号房屋（金额 = 2）, 因为他们是相邻的。

💎示例 2：

输入：nums = [1,2,3,1]
输出：4
解释：你可以先偷窃 1 号房屋（金额 = 1），然后偷窃 3 号房屋（金额 = 3）。
偷窃到的最高金额 = 1 + 3 = 4 。

💎示例 3：

输入：nums = [0]
输出：0

📜提示：

• 1 <= nums.length <= 100
• 0 <= nums[i] <= 1000

---

2.打家劫舍Ⅱ思路分析

🔗直达打家劫舍①链接，默认读者已经搞懂了打家劫舍①.

该问题是在打家劫舍①的基础上，添加了一个循环结构。如果你已经理解了打家劫舍①，那么这个Ⅱ只需要考虑怎么解决这个循环问题即可，也就是第一个数据和最后一个数据不能同时出现，要么最大金额只包含第一个数据，要么只包含最后一个数据。

所以我们可以将数组分为两部分，各自找出每一部分的最大金额，然后返回它们两个金额最大的即可【你会发现这样分为两部分之后，就不会出现第一个和最后一个数据同时出现的问题了；然后每一部分的解题过程就和打家劫舍1一模一样了。

---

3.暴力解法-递归实现

📕流程

（1）将数组分为两部分即可

• 0 ~ n - 1
• 1 ~ n

（2）然后将每一部分按照打家劫舍Ⅰ求解即可
（3）返回这两部分结果的最大值

    public int rob(int[] nums) 
        int l = nums.length;
        if (l == 1) 
            return nums[0];
        
        if (l == 2) 
            return Math.max(nums[0], nums[1]);
        
        int[] preNums = new int[l - 1];
        int[] sufNums = new int[l - 1];
        for (int i = 0; i < l - 1; i++) 
            preNums[i] = nums[i];
            if (i > 0) 
                sufNums[i - 1] = nums[i];
            
        
        sufNums[l - 2] = nums[l - 1];
        //以上代码是将数组分为两个子数组【1~n,0~n-1】
        preNums[1] = Math.max(preNums[0], preNums[1]);
        sufNums[1] = Math.max(sufNums[0], sufNums[1]);
		//以上两行与打家劫舍1类似
        return Math.max(recursion(preNums.length - 1, preNums), recursion(sufNums.length - 1, sufNums));
    
    public int recursion(int n, int[] nums) 
        if (n == 0 || n == 1) 
            return nums[n];
        
        return Math.max(recursion(n - 1, nums), recursion(n - 2, nums) + nums[n]);
    

当我将该暴力解法提交到LeetCode，发现会超时。


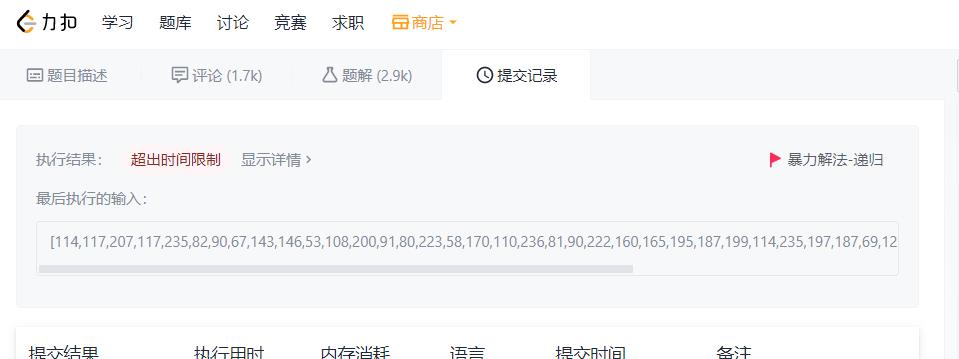
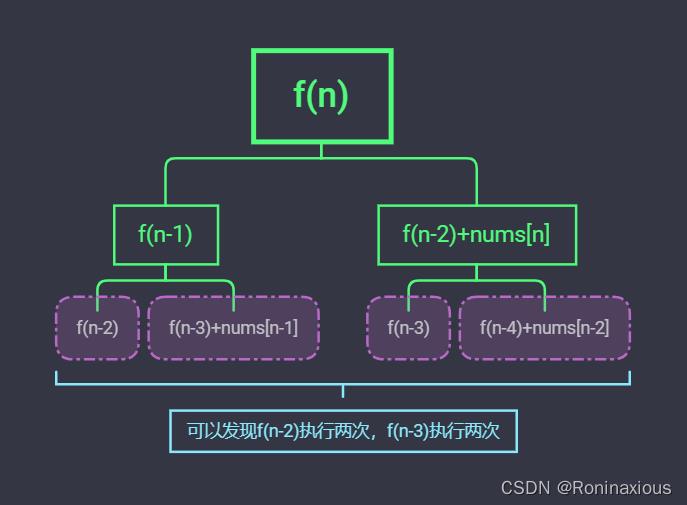
从上图我们可以看出使用递归出现了大量的重复计算（我只是枚举前三行，越往后重复越多），这是递归比较忌讳的问题之一（重复和栈溢出）。这样无异于在浪费CPU的运算单元。

复杂度分析：
空间复杂度：O(n)【每个栈空间复杂度为O(1)】O(n*1)=O(n)
时间复杂度：O(n^n)

• 递归算法的空间复杂度与所生成的最大递归树的深度成正比。如果递归算法的每个函数调用都占用 O(m) 空间,并且如果递归树的最大深度为 n,则递归算法的空间复杂度将为 O(n·m)。”

💌上述中递归解题方式的缺点就是重复量比较多，所以我们可以可以将途中计算的结果保存下来，俗称记忆集或记忆化搜索。此时你应该想到这不正是动态规划嘛。

---

4.记忆化搜索-动态规划

需要两个dp数组进行保存，因为在抽象层面分为两个数组了嘛，所以要使用两个记忆集。其他就和打家劫舍1一样了。

循环体内部包含两部分

• 0 ~ n-1
• 1 ~ n

    public int rob2(int[] nums) 
        if (nums.length == 1) 
            return nums[0];
        
        if (nums.length == 2) 
            return Math.max(nums[0], nums[1]);
        
        int[] dp1 = new int[nums.length - 1];
        dp1[0] = nums[0];
        dp1[1] = Math.max(nums[0], nums[1]);
        int[] dp2 = new int[nums.length - 1];
        dp2[0] = nums[1];
        dp2[1] = Math.max(nums[1], nums[2]);
        for (int i = 2; i < nums.length - 1; i++) 
        	//0~n-1
            dp1[i] = Math.max(dp1[i - 1], dp1[i - 2] + nums[i]);
            //1~n
            dp2[i] = Math.max(dp2[i - 1], dp2[i - 2] + nums[i + 1]);
        
        return Math.max(dp1[nums.length - 2], dp2[nums.length - 2]);
    

复杂度分析

空间复杂度为O(n)
时间复杂度为O(n)

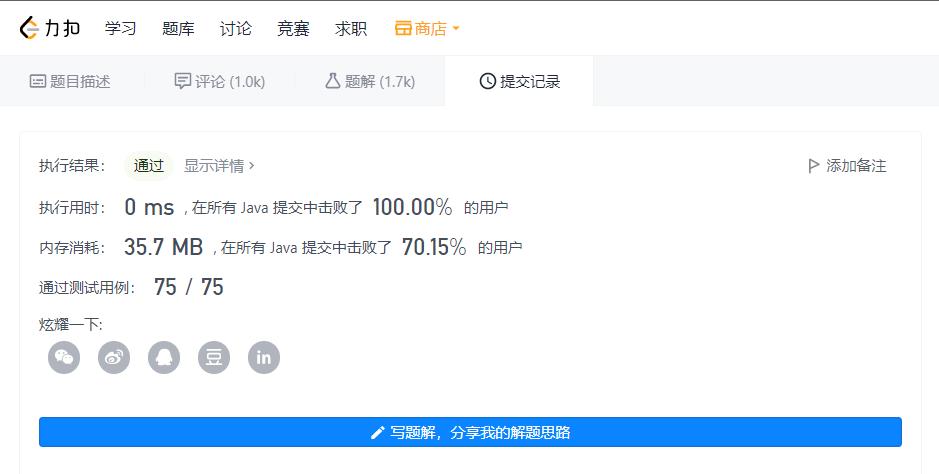
当我提交LeetCode上时，可以发现通过了。
分析一下：能不能将空间复杂度优化成O(1)呢？

---

5.动态规划之优化空间复杂度

如果理解了打家劫舍1和前面的流程，这个应该很简单。

    public int rob3(int[] nums) 
        if (nums.length == 1) 
            return nums[0];
        
        if (nums.length == 2) 
            return Math.max(nums[0], nums[1]);
        
        int pre1 = nums[0], pre2 = nums[1];
        int suf1 = Math.max(nums[0], nums[1]);
        int suf2 = Math.max(nums[1], nums[2]);
        int maxMoney1 = suf1;
        int maxMoney2 = suf2;
        for (int i = 2; i < nums.length - 1; i++) 
            maxMoney1 = Math.max(pre1 + nums[i], suf1);
            pre1 = suf1;
            suf1 = maxMoney1;
            maxMoney2 = Math.max(pre2 + nums[i + 1], suf2);
            pre2 = suf2;
            suf2 = maxMoney2;
        
        return Math.max(maxMoney1, maxMoney2);
    

复杂度分析

时间复杂度：O(n）
空间复杂度：O(1)

提交到LeetCode，当然能通过