模幂运算问题，使用朴素算法和重复-平方算法（快速幂+C#计算程序运行时间）

Posted 2022-01-01 小哈里

1、什么是模幂运算问题

• 给出a, k, mod
• 计算$a^k（\%mod）$的值
• k是一个非常大的正整数（超过1e7）

附，一个可以提交的地方：
leetcode 372. 超级次方

class Solution 
public:
    int pows(int a, int k)
        a %= 1337;
        if(k==0)return 1;
        int pp = pows(a,k/2)%1337;
        if(k%2==1)return pp*pp%1337*a%1337;
        else return pp*pp%1337;
    
    int superPow(int a, vector<int>& b) 
        if(b.empty())return 1;
        int last = b.back();  b.pop_back();
        return pows(a,last)*pows(superPow(a,b),10)%1337;
    
;

2、解决方法

朴素算法：

• 循环k次，每次乘上a，模上mod就行。

重复-平方算法：

• 即快速幂，有递归写法和非递归写法
• 递归做法的递推公式如下：
  
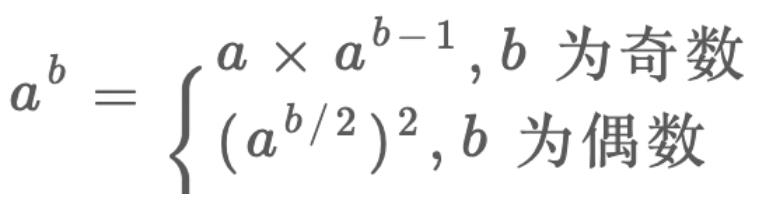
• 循环做法：
  将k表示为二进制，即每次最后一位为1，就是奇数，否则为偶数，不断右移，模拟递归过程，继续用上面的公式即可。。

附GUI效果图：

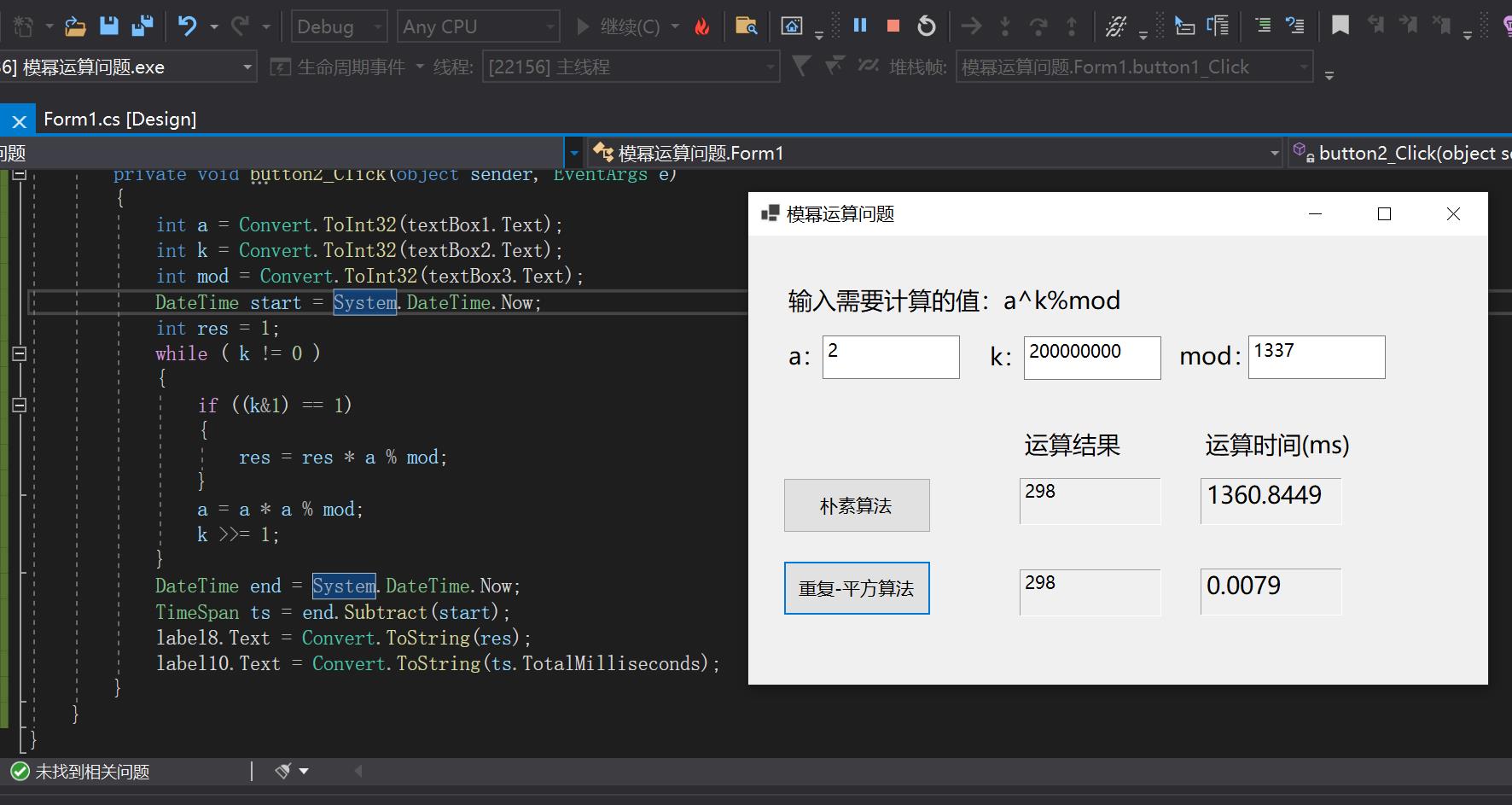
C#代码：

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;
using System.Timers;

namespace 模幂运算问题

    public partial class Form1 : Form
    
        public Form1()
        
            InitializeComponent();
        
        
        private void button1_Click(object sender, EventArgs e)
        
            int a = Convert.ToInt32(textBox1.Text);
            int k = Convert.ToInt32(textBox2.Text);
            int mod = Convert.ToInt32(textBox3.Text);
            DateTime start = System.DateTime.Now;
            int res = 1;
            for(int i = 1; i <= k; i++)
            
                res *= a;
                res %= mod;
            
            DateTime end = System.DateTime.Now;
            TimeSpan ts = end.Subtract(start);
            label7.Text = Convert.ToString(res);
            label9.Text = Convert.ToString(ts.TotalMilliseconds);
        

        private void button2_Click(object sender, EventArgs e)
        
            int a = Convert.ToInt32(textBox1.Text);
            int k = Convert.ToInt32(textBox2.Text);
            int mod = Convert.ToInt32(textBox3.Text);
            DateTime start = System.DateTime.Now;
            int res = 1;
            while ( k != 0 )
            
                if ((k&1) == 1)
                
                    res = res * a % mod;
                
                a = a * a % mod;
                k >>= 1;
            
            DateTime end = System.DateTime.Now;
            TimeSpan ts = end.Subtract(start);
            label8.Text = Convert.ToString(res);
            label10.Text = Convert.ToString(ts.TotalMilliseconds);