贪心思想及其题目,来刷吧
Posted 两片空白
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了贪心思想及其题目,来刷吧相关的知识,希望对你有一定的参考价值。
前言
之前觉得贪心思想,根本就总结不出一种规律。虽然这种题思想都是一个,但是,情况太多了。感觉这种题,很难想到。要不就是常识,要不想都想不到。这种题就是要看自己有没有刷过,并且还要能记住。
但是,细细体会。才会让你跟好的理解这种题的解题思路。至少,能让你很好的理解你刷的贪心题目。
贪心思想:
局部最优,推导出全局最优。
简单点说就是,每一次都取得最优的结果。最终的结果一定就会得到最优的结果。
比如:有很多钞票,规定次数,最后得到价值最大。解法:就是,每一次拿价值最大的钞票(局部最优),最后价值会最大(全局最优)。
主要就是想到,局部最优。
题目
基础
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
示例 1:输入: g = [1,2,3], s = [1,1]
输出: 1
解释:
你有三个孩子和两块小饼干,3个孩子的胃口值分别是:1,2,3。
虽然你有两块小饼干,由于他们的尺寸都是1,你只能让胃口值是1的孩子满足。
所以你应该输出1。
局部最优:每一次都拿最大的饼干,去喂给胃口最大,并且可以满足的孩子。
整体最优:满足孩子数最多。
class Solution
public:
int findContentChildren(vector<int>& g, vector<int>& s)
//贪心,将最大的饼干给胃口最大,并且能满足的孩子
//排序,最大在后面,最小在前面
sort(g.begin(), g.end());
sort(s.begin(), s.end());
int len1 = g.size();
int len2 = s.size();
int count = 0;
int j = len1-1;
for(int i =len2-1; i>=0; i--)
//找胃口最大的
for(; j>=0; j--)
if(g[j] <= s[i])
//找到
count++;
j--;
break;
if(j < 0)
//没有学生了
break;
return count;
;摆动序列
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 摆动序列 。第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。
例如, [1, 7, 4, 9, 2, 5] 是一个 摆动序列 ,因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。
相反,[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
子序列 可以通过从原始序列中删除一些(也可以不删除)元素来获得,剩下的元素保持其原始顺序。给你一个整数数组 nums ,返回 nums 中作为 摆动序列 的 最长子序列的长度 。
示例 1:
输入:nums = [1,7,4,9,2,5]
输出:6
解释:整个序列均为摆动序列,各元素之间的差值为 (6, -3, 5, -7, 3) 。
画成图,情况会是这样:
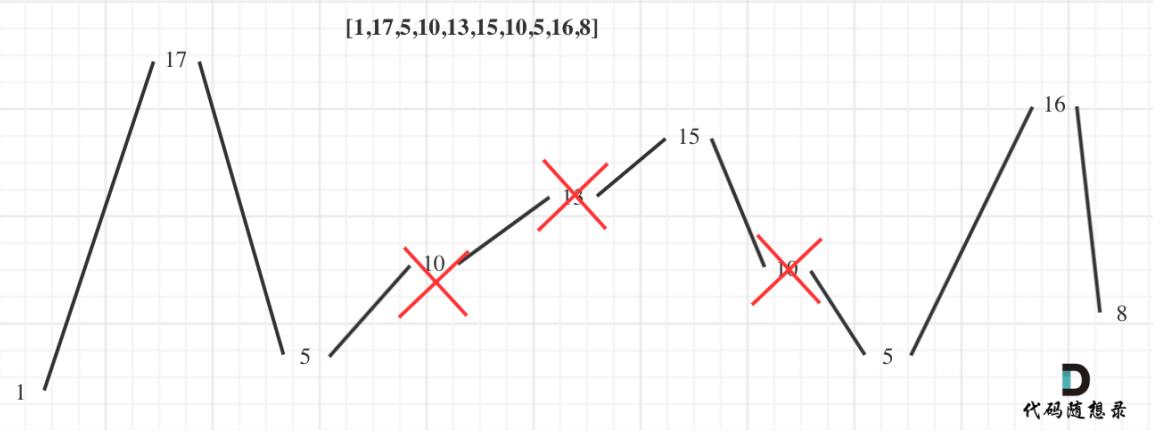
局部最优:找到单调序列里的最大值和最小值。即删除单调序列里的中间值。
整体最优:摆动序列长度最长。
特殊情况:
根据题意,数组只有一个或者两个元素也构成摆动序列。于是需要定起始就有一个摆动序列。
并且:
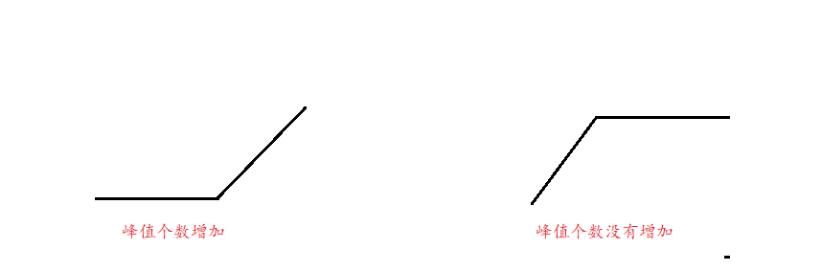
解法:比较前后差值,正负交替,或者前面为0,摆动序列数加1。
class Solution
public:
int wiggleMaxLength(vector<int>& nums)
//贪心思想,局部最优,找到单调的最高和最低点、删除单调不是最高最低点的值。
//整体才能得到最大长度
int res = 1;//只有一个值的情况
int len = nums.size();
if(len == 1)
return res;
//first最低点前一个差值
int first = nums[1] - nums[0];
//两个值的情况
if(first)
res++;
//最高点差值
int second = 0;
for(int i=2; i<len; i++)
//找最高点
second = nums[i] - nums[i-1];
if((first <= 0 &&second > 0)||(first >= 0 && second < 0))
//更新最低点
first = second;
res++;
return res;
;最大子序和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
局部最优:找到每一次正数和的最大值。
当和加到为负数时,这个和成为了下一次和的负担。会拖累下一次的总和。需要从0开始加。
整体最优:找到整体最大和。
class Solution
public:
int maxSubArray(vector<int>& nums)
int res = INT_MIN;
int sum = 0;
for(int i= 0; i<nums.size(); i++)
sum+=nums[i];
//最大子序和
if(sum > res)
res = sum;
//和为负数,需要从0开始加
if(sum < 0)
sum=0;
return res;
;股票的最大利润
假设把某股票的价格按照时间先后顺序存储在数组中,请问买卖该股票一次可能获得的最大利润是多少?
示例 1:
输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。
注意:只能一次买卖。
贪心算法:
局部最优:每次选出前面的最小买入价格。当前卖出,每次当前值和最小卖出价格的利润的最大值。
全局最优:得到最大利润。
class Solution
public:
int maxProfit(vector<int>& prices)
//最小买入点
int pmin = INT_MAX;
//最大利润
int pmax = 0;
int len = prices.size();
for(int i =0; i<len; i++)
//找前面最小买入点
if(pmin > prices[i])
pmin = prices[i];
//当前卖出的最大利润
if(pmax < prices[i] - pmin)
pmax = prices[i] - pmin;
return pmax;
;买卖股票的最佳时机II
给定一个数组 prices ,其中 prices[i] 是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: prices = [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
贪心算法:
局部最优:在最低是买入,在最高时卖出。完后如此循环。
全局最优:会得到最大的利润。
怎么才是最高和最低呢?
在一段区间内,单调递增,找到最高点和最低点。计算差值。
class Solution
public:
int maxProfit(vector<int>& prices)
//贪心算法
int res = 0;
int i = 1;
while(i<prices.size())
if(prices[i] > prices[i-1])
//最低价格
int minprice = prices[i-1];
while(i< prices.size() && prices[i] > prices[i-1])
i++;
//最高价格
int maxprice = prices[i-1];
//得到一段区间的最大利润
res += (maxprice - minprice);
else
i++;
return res;
;但是,其实,我们可以将每一个利润进行分解,分解成每天的利润。
比如:要求prices[3] - prices[0]的利润。可以分解成prices[3] - prices[2] + prices[2] - prices[1] + prices[1] - prices[0]。
要求单调递增的最大值和最小值的差。由于是单调递增,每天的利润一定会是正利润。将所有的正利润加起来就好了。
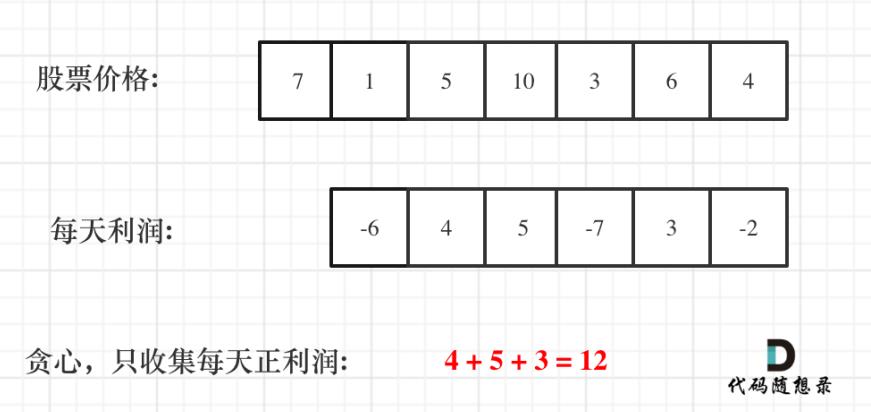
class Solution
public:
int maxProfit(vector<int>& prices)
//贪心算法
//局部最优:获得每天的 正利润
//整体最优:得到最大利润
int res = 0;
int money = 0;
for(int i =1; i<prices.size(); i++)
if(prices[i] - prices[i-1] > 0)
res += (prices[i] - prices[i-1]);
return res;
;跳跃游戏
给定一个非负整数数组 nums ,你最初位于数组的 第一个下标 。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标。
示例 1:
输入:nums = [2,3,1,1,4]
输出:true
解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
局部最优:选出当前范围内,下一次可以走的最大范围。
全局最优:得到最大范围。
结果:比较最大范围是否包含nums的最后一个下标。
范围就是索引对应索引对应的值,即i + nums[i]。
class Solution
public:
bool canJump(vector<int>& nums)
//贪心算法;
//局部最优:每次都选步数范围内的最大步数。
int len = nums.size();
int i = 0;
while(i < len)
int maxstep = i + nums[i];
//可以到达最后一个下标
if(maxstep >= len - 1)
return true;
//不可以到达最后一个下标
//nums[i] = 0
if(i == maxstep)
return false;
//选最大范围,范围等于j + nums[j]
int m = -1;
for(int j = i+1; j <= maxstep; j++)
if(m < j + nums[j])
i = j;
m = j + nums[j];
return true;
;跳跃游戏II
给你一个非负整数数组 nums ,你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
你的目标是使用最少的跳跃次数到达数组的最后一个位置。
假设你总是可以到达数组的最后一个位置。
示例 1:
输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
和上面一题如出一辙,不同的是,这一次肯定可以到达最后一个下标处,记录步数。
局部最优:选出当前范围内,下一次可以走的最大范围。
全局最优:得到最小步数。
范围就是索引对应索引对应的值,即i + nums[i]。
class Solution
public:
int jump(vector<int>& nums)
int len = nums.size();
//不需要跳
if(len == 1)
return 0;
int i = 0;
//初始化为1,最后一跳
int step = 1;
while(i < len)
//最大范围
int maxcover = i + nums[i];
//到达最后一个下标
if(maxcover >= len - 1)
break;
//找最大范围
int m = -1;
for(int j = i+1; j <= maxcover; j++)
if(m < j + nums[j])
i = j;
m = j + nums[j];
//步数加1
step++;
return step;
;K次取反后最⼤化的数组和
给你一个整数数组 nums 和一个整数 k ,按以下方法修改该数组:
选择某个下标 i 并将 nums[i] 替换为 -nums[i] 。
重复这个过程恰好 k 次。可以多次选择同一个下标 i 。以这种方式修改数组后,返回数组 可能的最大和 。
示例 1:
输入:nums = [4,2,3], k = 1
输出:5
解释:选择下标 1 ,nums 变为 [4,-2,3] 。
贪心算法:
注意:数字可以重复选取。
局部最优:每次让负数转变为正数,如果为0并且没有负数,让0变符号K次。
整体最优:得到的数组和为最大值。
当上面变化完之后,K还是大于0。还需要使用贪心算法。
注意:上面情况变化完之后,没有负数了。
局部最优:如果K为负数,让最小值为负数,意思就是让最小值变化符号K次。
整体最优:数组和最大。
注意:再变符号前,先将数组排好序。
class Solution
public:
int largestSumAfterKNegations(vector<int>& nums, int k)
sort(nums.begin(), nums.end());
int len = nums.size();
for(int i =0; i<len; i++)
//如果是负数,变为正数
if(k && nums[i] < 0)
k--;
nums[i] = -nums[i];
continue;
//如果是0,只让0变化就好了
if(nums[i] == 0)
k=0;
break;
//如果此时K>0且k为奇数,让最小值为负数就好了
if(k % 2)
int min = INT_MAX;
int pos = 0;
for(int i =0; i<len; i++)
if(min > nums[i])
min = nums[i];
pos = i;
nums[pos] = -nums[pos];
//求和
int sum = 0;
for(auto ch : nums)
sum += ch;
return sum;
;加油站
在一条环路上有 N 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
如果你可以绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1。
说明:
如果题目有解,该答案即为唯一答案。
输入数组均为非空数组,且长度相同。
输入数组中的元素均为非负数。
示例 1:输入:
gas = [1,2,3,4,5]
cost = [3,4,5,1,2]输出: 3
解释:
从 3 号加油站(索引为 3 处)出发,可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站,此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站,此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站,此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站,此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站,你需要消耗 5 升汽油,正好足够你返回到 3 号加油站。
因此,3 可为起始索引。
首先考虑清除,什么情况可以绕环路行驶一周。当消耗汽油和加的汽油数的差之和大于等于0时,说明可以环路一周。
起始位置怎么求,从0开始,走过一个站的剩余油数和小于0,说明不能做起始位置。
贪心算法:
局部最优:从0站开始,走到j站的剩余油数小于0,说明j不能做起始位置。起始位置从j+1开始。并且,剩余油数从j+1开始加。
全局最优:找到可以跑一圈的起始位置。
class Solution
public:
int canCompleteCircuit(vector<int>& gas, vector<int>& cost)
int len1 = gas.size();
int len2 = cost.size();
int sumrest = 0;//剩余总和
int rest = 0;//当前剩余汽油
int startpos = 0;//起始位置
for(int i =0; i<len1; i++)
sumrest += (gas[i] - cost[i]);
rest += (gas[i] - cost[i]);
//剩余汽油小于0,不能作为起始位置,起始位置在下一个
if(rest < 0)
rest = 0;
startpos = i + 1;
//sumrest >= 0说明可以环路一周
if(sumrest >= 0)
return startpos;
return -1;
;柠檬⽔找零
在柠檬水摊上,每一杯柠檬水的售价为 5 美元。顾客排队购买你的产品,(按账单 bills 支付的顺序)一次购买一杯。
每位顾客只买一杯柠檬水,然后向你付 5 美元、10 美元或 20 美元。你必须给每个顾客正确找零,也就是说净交易是每位顾客向你支付 5 美元。
注意,一开始你手头没有任何零钱。
给你一个整数数组 bills ,其中 bills[i] 是第 i 位顾客付的账。如果你能给每位顾客正确找零,返回 true ,否则返回 false 。
示例 1:
输入:bills = [5,5,5,10,20]
输出:true
解释:
前 3 位顾客那里,我们按顺序收取 3 张 5 美元的钞票。
第 4 位顾客那里,我们收取一张 10 美元的钞票,并返还 5 美元。
第 5 位顾客那里,我们找还一张 10 美元的钞票和一张 5 美元的钞票。
由于所有客户都得到了正确的找零,所以我们输出 true。
注意:是顺序收取。
一开始没有零钱,一开始卖出,收到的必须是5块。
有三种情况:
1. 收到5块,不需要找零,直接收取。
2. 收到10块,需要找零5块。
3. 收到20块,需要找零15块。
贪心思想:
局部最优:如果收到20块钱,优先找零10块和5块,因为5块的用处比10块多。
全局最优:可以找零成功
class Solution
public:
bool lemonadeChange(vector<int>& bills)
int fivecount = 0;
int tencount = 0;
int twcount = 0;
int len = bills.size();
if(bills[0] != 5)
return false;
for(int i =0; i < len; i++)
if(bills[i] == 5)
fivecount++;
else if(bills[i] == 10)
if(fivecount == 0)
return false;
else
tencount++;
fivecount--;
else
//bills[i] == 20
if(tencount > 0 && fivecount > 0)
//先还10块加5块的,5块用处更多
tencount--;
fivecount--;
twcount++;
else if(fivecount >= 3)
fivecount -= 3;
twcount++;
else
return false;
return true;
;根据身⾼重建队列
假设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ,前面 正好 有 ki 个身高大于或等于 hi 的人。
请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ,其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性(queue[0] 是排在队列前面的人)。
示例 1:
输入:people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
输出:[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
解释:
编号为 0 的人身高为 5 ,没有身高更高或者相同的人排在他前面。
编号为 1 的人身高为 7 ,没有身高更高或者相同的人排在他前面。
编号为 2 的人身高为 5 ,有 2 个身高更高或者相同的人排在他前面,即编号为 0 和 1 的人。
编号为 3 的人身高为 6 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。
编号为 4 的人身高为 4 ,有 4 个身高更高或者相同的人排在他前面,即编号为 0、1、2、3 的人。
编号为 5 的人身高为 7 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。
因此 [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 是重新构造后的队列。
这个题有两个维度,一个维度是身高,一个维度是前面大于当前身高的人数。
我们需要先确定一个维度,通过另外一个维度来得到结果。
那我们是先确定身高还是人数呢?
如果确定人数,按照k从大到小排列。我们发现,身高仍会是无序的,并没有确定好一个条件。
先确定好身高,按照身高从高到低排列,身高相同,人数少的排前面。此时,就只需要按照K来进行排列就好了。
看下图:

此时,我们只需要按照K来进行插入到对应值的位置,前面高于当前身高的人数一定是正确的。
我们需要从大到小来进行插入,先处理好高身高的人。
贪心思想:
前提:按照身高从大到小排列,身高相同,人数少的排前面。
局部最优:按照人数,插入到对应位置。
全局最优:形成正确排列。
class Solution
static bool cmp(vector<int>& p1, vector<int>& p2)
return p1[0] > p2[0] || (p1[0] == p2[0] && p1[1] < p2[1]);
public:
vector<vector<int>> reconstructQueue(vector<vector<int>>& people)
int row = people.size();
vector<vector<int>> res;
sort(people.begin(), people.end(), cmp);
for(int i=0; i<row; i++)
//res[people[i][1]] = people[i];
//vector<int> tmp = people[i];
//people.erase(people.begin() + i);
//people.insert(people.begin() + tmp[1], tmp);
//cout<<i<<endl;
res.insert(res.begin() + people[i][1], people[i]);
//cout<<i<<endl;
return res;
;我们知道数组插入数据,需要挪动数据,效率不是很高,而链表插入数据可以直接插入。
我们可以先用链表来形成队列。
class Solution
static bool cmp(vector<int>& p1, vector<int>& p2)
return p1[0] > p2[0] || (p1[0] == p2[0] && p1[1] < p2[1]);
public:
vector<vector<int>> reconstructQueue(vector<vector<int>>& people)
//先将ki为0,且最小的排前面
int row = people.size();
//不需要初始化
list<vector<int>> ls;
sort(people.begin(), people.end(), cmp);
//从身高高的开始插入,按照k插入
//前面会正好
for(int i=0; i<row; i++)
auto it = ls.begin();
int pos = people[i][1];
//ls.insert(ls.begin() + pos, people[i]);不可以,因为list不连续
while(pos--)//寻找插入位置
it++;
ls.insert(it, people[i]);
vector<vector<int>> res;
for(auto ch : ls)
res.push_back(ch);
return res;
;⽤最少数量的箭引爆⽓球
在二维空间中有许多球形的气球。对于每个气球,提供的输入是水平方向上,气球直径的开始和结束坐标。由于它是水平的,所以纵坐标并不重要,因此只要知道开始和结束的横坐标就足够了。开始坐标总是小于结束坐标。
一支弓箭可以沿着 x 轴从不同点完全垂直地射出。在坐标 x 处射出一支箭,若有一个气球的直径的开始和结束坐标为 xstart,xend, 且满足 xstart ≤ x ≤ xend,则该气球会被引爆。可以射出的弓箭的数量没有限制。 弓箭一旦被射出之后,可以无限地前进。我们想找到使得所有气球全部被引爆,所需的弓箭的最小数量。
给你一个数组 points ,其中 points [i] = [xstart,xend] ,返回引爆所有气球所必须射出的最小弓箭数。
示例 1:输入:points = [[10,16],[2,8],[1,6],[7,12]]
输出:2
解释:对于该样例,x = 6 可以射爆 [2,8],[1,6] 两个气球,以及 x = 11 射爆另外两个气球
这个的贪心思想很容易想到:
局部最优:选出范围重叠个数最多的气球。
全局最优:针数最少。
但是,怎么使得重叠的范围最多呢?这个不容易想到。
首先,我们需要对区间排好序,可以按照范围的起始值排序。
其次,找重叠区间在于,气球的起始值在重叠区间的最小结束值里,即小于等于重叠区间最小结束值。
当不在重叠区间里时,需要加一根针。
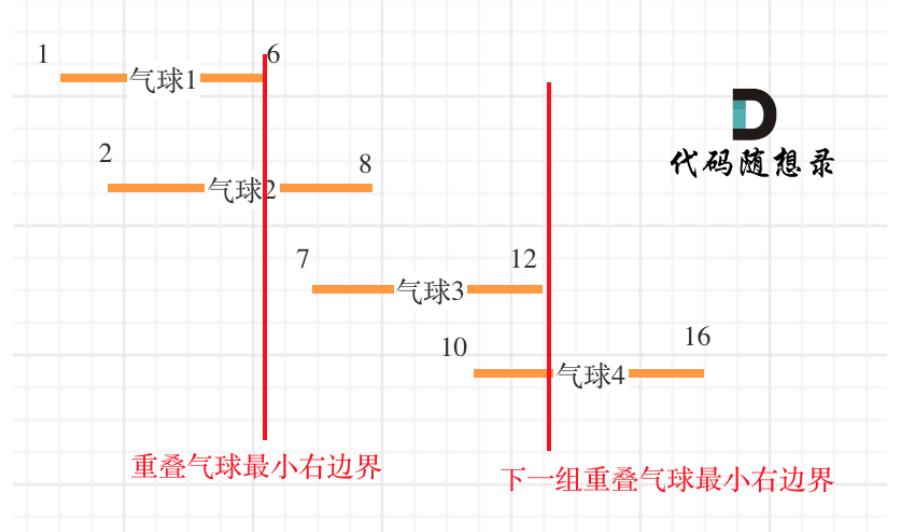
class Solution
static bool cmp(vector<int>& p1, vector<int>& p2)
return p1[0] < p2[0];
public:
int findMinArrowShots(vector<vector<int>>& points)
if(points.size() == 0)
return 0;
sort(points.begin(), points.end(), cmp);
//有气球,一定需要一根针
int count = 1;
for(int i =1; i<points.size(); i++)
if(points[i][0] > points[i-1][1])
//不在重叠区间里,需要加一根针
count++;
else
//在重叠区间里
//找最小重叠区间结束值
points[i][1] = min(points[i][1], points[i-1][1]);//下一次循环就会是points[i][1]
return count;
;⽆重叠区间
给定一个区间的集合,找到需要移除区间的最小数量,使剩余区间互不重叠。
注意:
可以认为区间的终点总是大于它的起点。
区间 [1,2] 和 [2,3] 的边界相互“接触”,但没有相互重叠。
示例 1:输入: [ [1,2], [2,3], [3,4], [1,3] ]
输出: 1
解释: 移除 [1,3] 后,剩下的区间没有重叠。
和上题思想差不多。
贪心思想:
局部最优:计算出每个重复区间的个数减1的和。
全局最优:需要移除区间个数。
怎么计算重复区间个数?
首先,按照左边界从小到大排序。
其次,找重复区间个数,记录重复区间的最小右边界。当当前区间左边界小于右边界时,重复区间数加1。
class Solution
static bool cmp(vector<int>& p1, vector<int>& p2)
return p1[0] < p2[0];
public:
int eraseOverlapIntervals(vector<vector<int>>& intervals)
//找出 重叠的区间个数
sort(intervals.begin(), intervals.end(), cmp);
int count = 0;//记录重复区间个数
for(int i = 1; i < intervals.size(); i++)
//每个重复区间个数都会减1,第一个没算进去
if(intervals[i][0] < intervals[i - 1][1])
//重复
count++;
//记录区间最小值
intervals[i][1] = min(intervals[i][1], intervals[i-1][1]);
return count;
;
借鉴:「代码随想录」贪⼼算法专题精讲
以上是关于贪心思想及其题目,来刷吧的主要内容,如果未能解决你的问题,请参考以下文章