算法入门（回溯算法）

Posted 2022-01-01 韶光不负

当学习完递归后，就可以来学习与理解它好兄弟回溯了。回溯算法比较抽象，小编就以自己学习的角度来分析了！

 

回溯与递归有什么关系 

递归与回溯是相辅相成的，回溯算法在递归之后，（可以理解没有递归就没有回溯，递归下不一定使用回溯算法，要根据问题）

什么是回溯算法

回溯算法是一个暴力的搜索算法。回溯就是一个递归的过程

按选优条件向前搜索，以达到目标。 但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术，而满足回溯条件的某个状态的点称为"回溯点"。

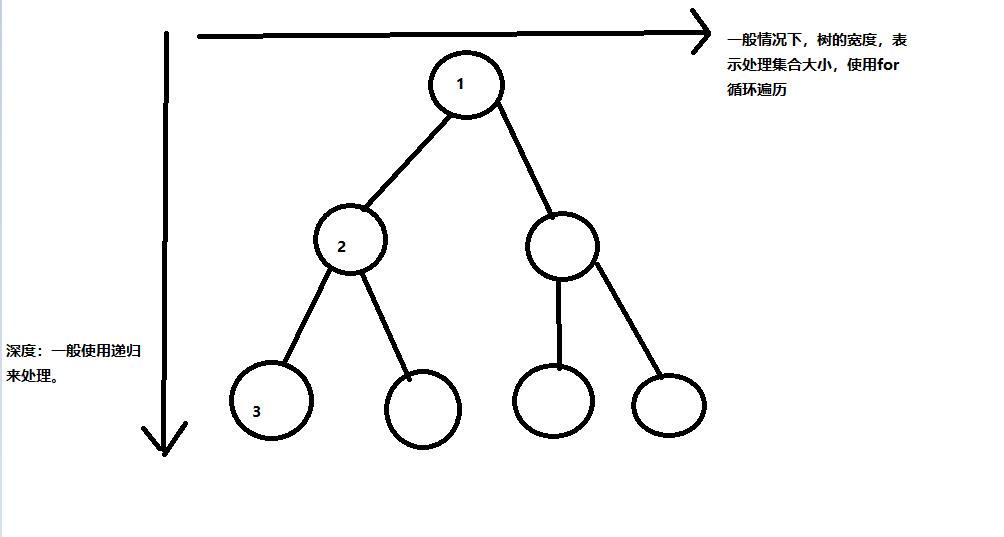
所有的回溯法可以抽象为一个树形结构

如下图二叉树

回溯算法模板

void backtracking(参数) 
     if (终⽌条件) 
     存放结果;
     return;
     
     for (选择：本层集合中元素（树中节点孩⼦的数量就是集合的⼤⼩）) 
           处理节点;
         backtracking(路径，选择列表); // 递归
         回溯，撤销处理结果
     

回溯算法能解决的题目

数组（leetcode 39,40,216），切割(140)，子集(78,90)，组合(46,47)，少数棋盘（如n皇后(51)，n数组问题）

数组总和（leetcode）

class Solution 
    List<List<Integer>> list = new ArrayList<>();
    List<Integer> list1 = new ArrayList<>();
    public List<List<Integer>> combinationSum(int[] candidates, int target) 
        Arrays.sort(candidates);
        helper(candidates,0,target);
        return list;
    
    public void helper(int[] cand , int start ,int target)
        int len = cand.length;
        if (target == 0)
            list.add(new ArrayList<Integer>(list1));
            return;
        
        for (int i = start; i < len ; i++) 
            if (cand[i] > target) break;
            list1.add(cand[i]);
            helper(cand,i,target - cand[i]);
            list1.remove(list1.size()-1);
        
    

全排列（46）

class Solution 
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> output = new ArrayList<>();
    public List<List<Integer>> permute(int[] nums) 
        for (int num : nums) 
            output.add(num);
        

        int n = nums.length;
        backtrack(n, output, res, 0);
        return res;
    
    public void backtrack(int n, List<Integer> output, List<List<Integer>> res, int first) 
        // 所有数都填完了
        if (first == n) 
            res.add(new ArrayList<Integer>(output));
        
        for (int i = first; i < n; i++) 
            // 动态维护数组
            Collections.swap(output, first, i);
            // 继续递归填下一个数
            backtrack(n, output, res, first + 1);
            // 撤销操作
            Collections.swap(output, first, i);
        
    

n皇后

package com.itheima;


import java.util.ArrayList;
import java.util.List;

class Solution 
    
    int[] arr;
    List<List<String>> res = new ArrayList<>();
    public List<List<String>> solveNQueens(int n) 
        arr = new int[n];
        dnf(n,0);
        return res;
    
    public void dnf(int n , int index)
        if (n == index)
            ArrayList<String> list = new ArrayList<>();
            for (int i = 0; i < n;i++)
                StringBuilder str =new StringBuilder();
                for (int j = 0; j < n ; j++) 
                    if (arr[i] == j)
                        str.append('Q');

                    else 
                        str.append('.');
                    
                
                list.add(new String(str));
            
            res.add(list);
            return;
         else
            for (int i = 0; i < n ; i++) 
                arr[index] = i;
                if (judge(index))
                    dnf(n,index+1);
                
            
        

    
    private boolean judge(int index) 
        for (int i = 0; i < index; i++) 
            if (arr[i] == arr[index] || Math.abs(i - index) == Math.abs(arr[i] - arr[index])) 
                return false;
            
        
        return true;