剑指 Offer 59 - I. 滑动窗口的最大值 c++/java详细题解

Posted 2022-01-01 林深时不见鹿

目录

• • • 1、题目
    • 2、思路
    • 3、c++代码
    • 4、java代码

1、题目

给定一个数组 nums 和滑动窗口的大小 k，请找出所有滑动窗口里的最大值。

示例:

输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7] 
解释: 

  滑动窗口的位置                最大值

-------------------------     -----

[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

提示：

你可以假设 k 总是有效的，在输入数组不为空的情况下，1 ≤ k ≤ 输入数组的大小。

2、思路

(单调队列) $O(n)$

给定一个数组 nums 和滑动窗口的大小 k，让我们找出所有滑动窗口里的最大值。

样例：

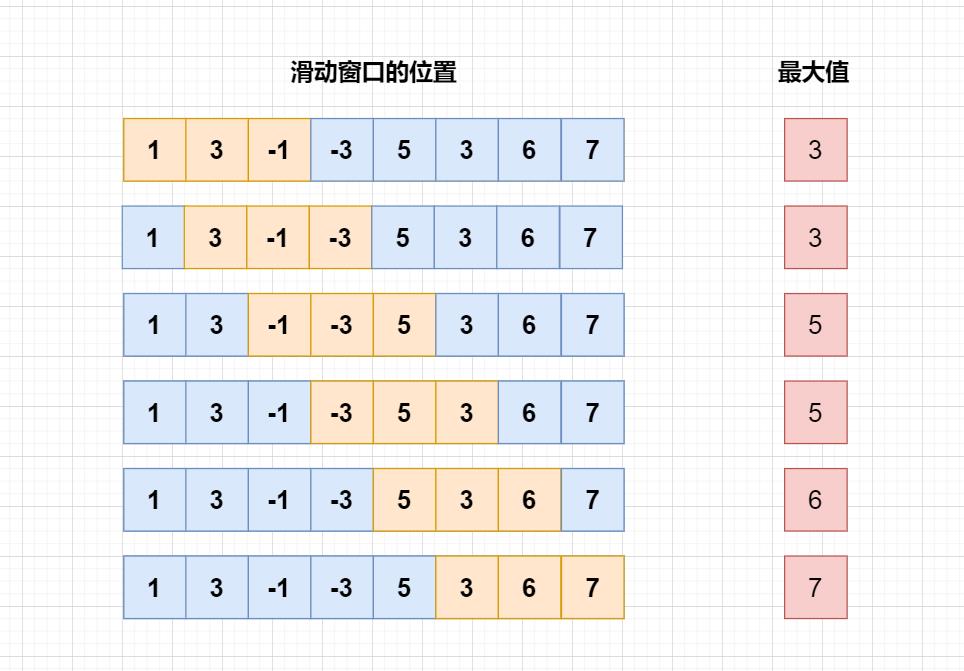
如样例所示，nums = [1,3,-1,-3,5,3,6,7]，k = 3，我们输出[3,3,5,5,6,7]。

首先，我们可以想到最朴素的做法是模拟滑动窗口的过程，每向右滑动一次都遍历一遍滑动窗口，找到最大的元素输出，这样的时间复杂度是$O(nk)$。考虑优化，其实滑动窗口类似于数据结构双端队列，窗口向右滑动过程相当于向队尾添加新的元素，同时再把队首元素删除。

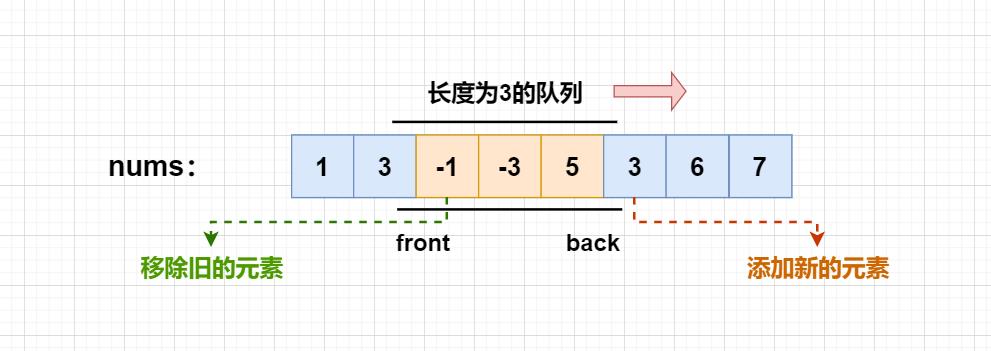
如何更快的找到队列中的最大值？

其实我们可以发现，队列中没必要维护窗口中的所有元素，我们可以在队列中只保留那些可能成为窗口中的最大元素，去掉那些不可能成为窗口中的最大元素。

考虑这样一种情况，如果新进来的数字大于滑动窗口的末尾元素，那么末尾元素就不可能再成为窗口中最大的元素了，因为这个大的数字是后进来的，一定会比之前先进入窗口的小的数字要晚离开窗口，因此我们就可以将滑动窗口中比其小的数字弹出队列，于是队列中的元素就会维持从队头到队尾单调递减，这就是单调递减队列。

单调递增队列

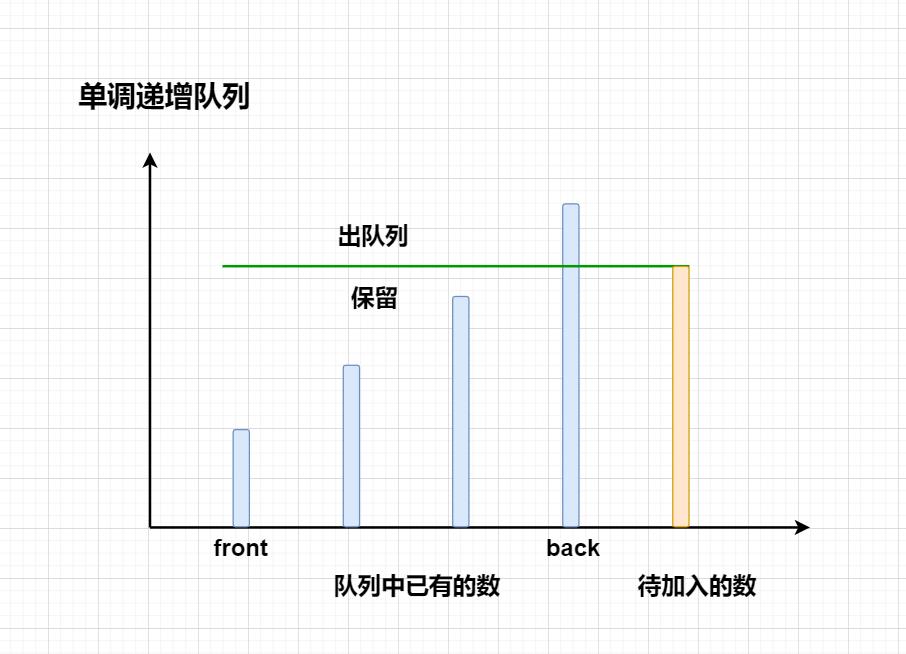
对于队列内的元素来说：

1. 在队列内自己左边的数就是数组中左边第一个比自己小的元素。
2. 当被弹出时，遇到的就是数组中右边第一个比自己小的元素 。( 只要元素还在队列中，就意味着暂时还没有数组中找到自己右侧比自己小的元素)
3. 队头到队尾单调递增，队首元素为队列最小值。

单调递减队列

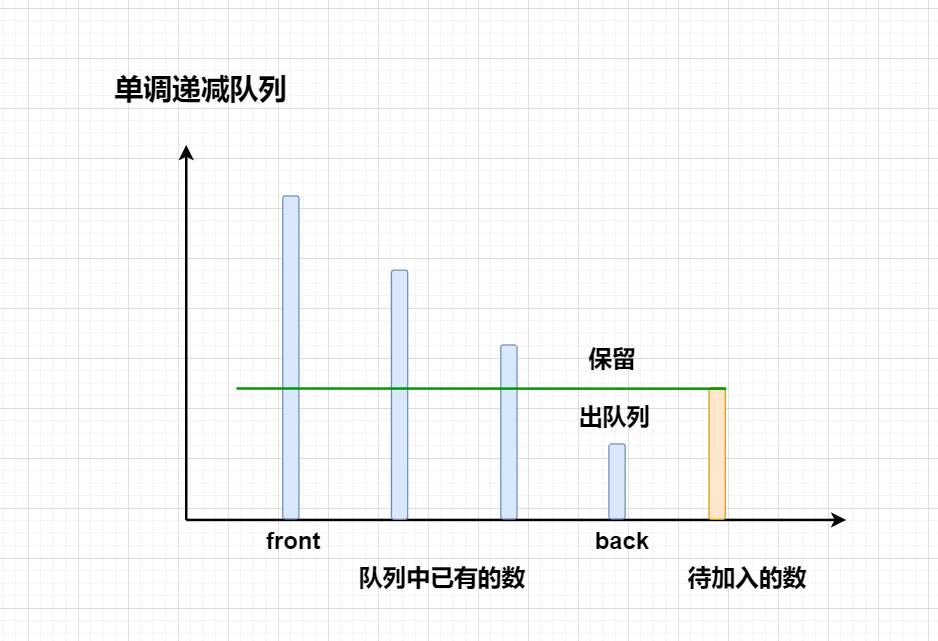
对于队列内的元素来说：

1. 在队列内自己左边的数就是数组中左边第一个比自己大的元素。
2. 当被弹出时，遇到的就是数组中右边第一个比自己大的元素 ，只要元素还在队列中，就意味着暂时还没有数组中找到自己右侧比自己大的元素。
3. 队头到队尾单调递减，队首元素为队列最大值。

了解了单调队列的一些性质以后，对于这道题我们就可以维护一个单调递减队列，来保存队列中所有递减的元素 ，随着入队和出队操作实时更新队列，这样队首元素始终就是队列中的最大值。同时如果队首元素在滑动窗口中，我们就可以将其加入答案数组中。

实现细节：

为了方便判断队首元素与滑动窗口的位置关系，队列中保存的是对应元素的下标。

具体解题过程如下：

初始时单调队列为空，随着对数组的遍历过程中，每次插入元素前，需要考察两个事情：

• 1、合法性检查：队头下标如果距离i 超过了 k ，则应该出队。
• 2、单调性维护：如果 nums[i] 大于或等于队尾元素下标所对应的值，则当前队尾再也不可能充当某个滑动窗口的最大值了，故需要队尾出队，始终保持队中元素从队头到队尾单调递减。
• 3、如次遍历一遍数组，队头就是每个滑动窗口的最大值所在下标。

时间复杂度分析： 每个元素最多入队出队一次，复杂度为$O(n)$。

3、c++代码

class Solution 
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) 
        deque<int>q; //双端队列
        vector<int>res;
        for(int i = 0; i < nums.size(); i++)
            while(q.size() &&  i - k + 1 > q.front())  q.pop_front(); //判断队头是否在滑动窗口范围内
            while(q.size() && nums[i] >= nums[q.back()]) q.pop_back();//维护单调递减队列
            q.push_back(i); //将当前元素插入队尾
            if(i >= k - 1)  res.push_back(nums[q.front()]); //滑动窗口的元素达到了k个，才可以将其加入答案数组中
        
        return res;
    
;

4、java代码

class Solution 
    public int[] maxSlidingWindow(int[] nums, int k) 
        int n = nums.length;
        Deque<Integer> queue = new ArrayDeque<>(); //双端队列
        int[] res = new int[n - k + 1];
        for (int i = 0 , j = 0; i < n; i++) 
            //判断队头是否在滑动窗口范围内
            while (!queue.isEmpty() && i- k + 1 > queue.getFirst())   queue.pollFirst();
            //维护单调递减队列
            while (!queue.isEmpty() && nums[i] > nums[queue.getLast()])  queue.pollLast();
            queue.offer(i);    //将当前元素插入队尾
            //滑动窗口的元素达到了k个，才可以将其加入答案数组中
            if( i - k + 1 >= 0) res[j++] = nums[queue.getFirst()];           
        
        return res;
    

原题链接： 剑指 Offer 59 - I. 滑动窗口的最大值