AVL树（Java语言）

Posted 2021-12-30 啊qie！

平衡二叉树

平衡二叉树也叫平衡二叉查找树，又被称为AVL树，可以保证查询效率较高。它的特点是：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。
结点的平衡因子定义为：结点的左子树高度与右子树高度之差。显然，对一棵AVL树而言，其所有结点的平衡因子只能是-1，0，1.挡在一棵AVL树上插入一个结点时，有可能导致失衡，即出现绝对值大于1的平衡因子。

单旋转（左旋转）

插入70后失去平衡，调整过程如下：。

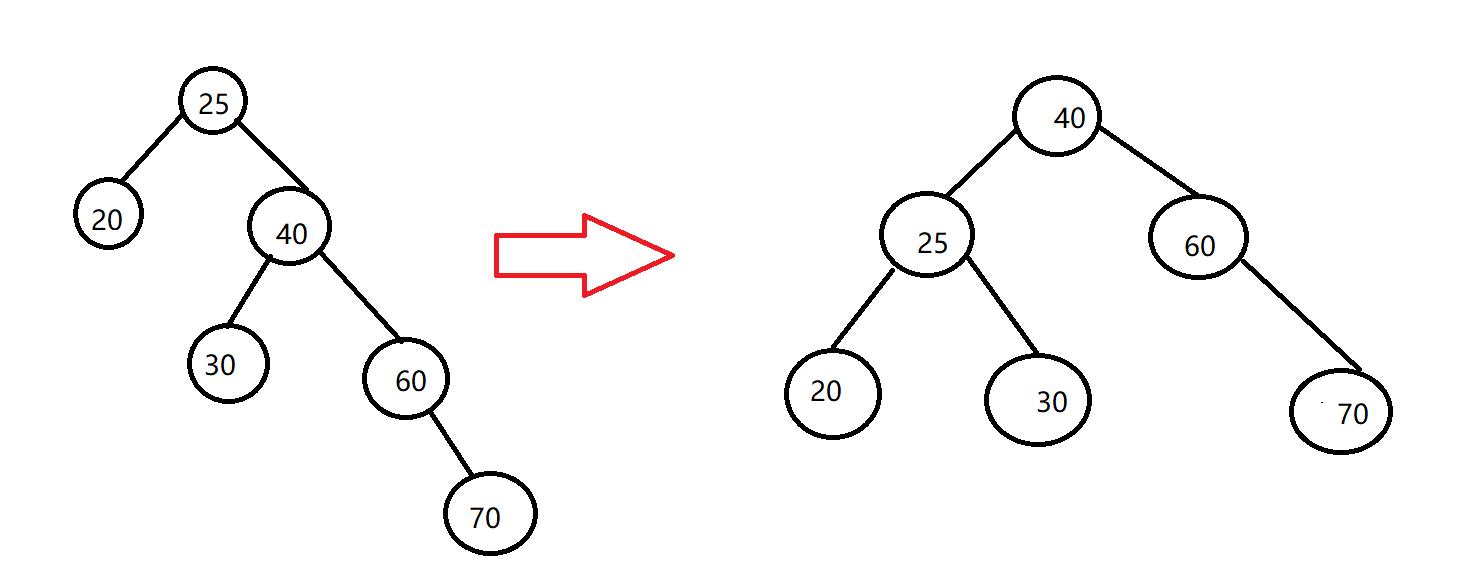
思路：
1、创建一个新的结点，值等于当前根节点的值。
2、把新节点的左子树设置为当前结点的左子树。
3、把新节点的右子树设置为当前节点的右子树的左子树。
4、把当前结点的值换为右子节点的值
5、把当前节点的右子树设置为当前节点右子树的右子树。
6、把当前结点的左子树（左子节点）设置为新节点

单旋转（右旋转）

插入15后失去平衡，调整过程如下：

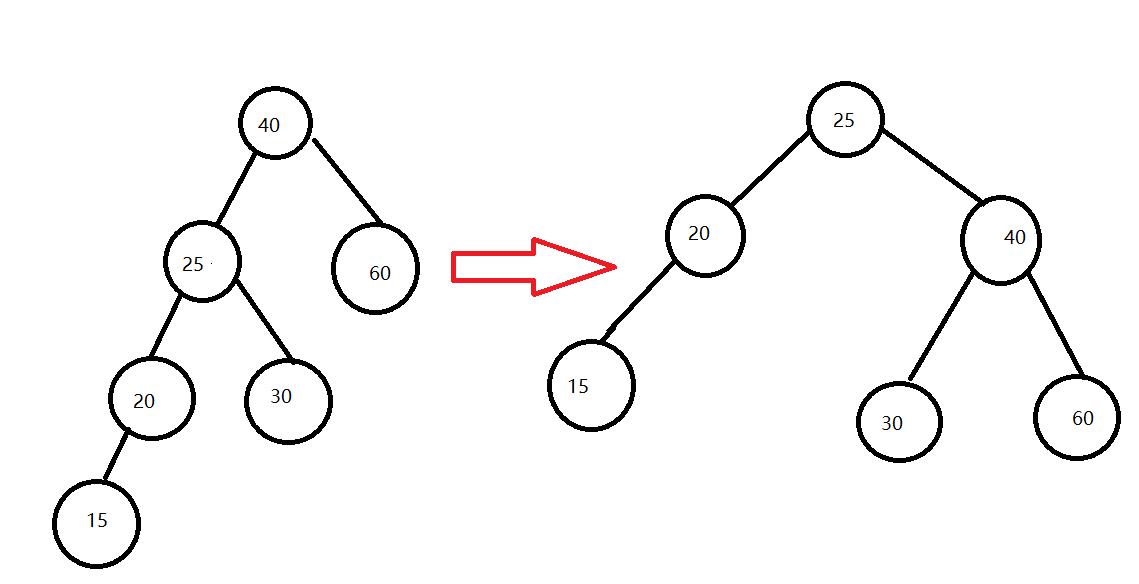
思路：
1、创建一个新的结点，值等于当前根节点的值。
2、把新节点的右子树设置为当前结点的右子树。
3、把新节点的左子树设置为当前节点的左子树的右子树。
4、把当前结点的值换为左子节点的值
5、把当前节点的左子树设置为当前节点左子树的左子树。
6、把当前结点的右子树（右子节点）设置为新节点

双旋转

情况一：当符合左旋转条件时

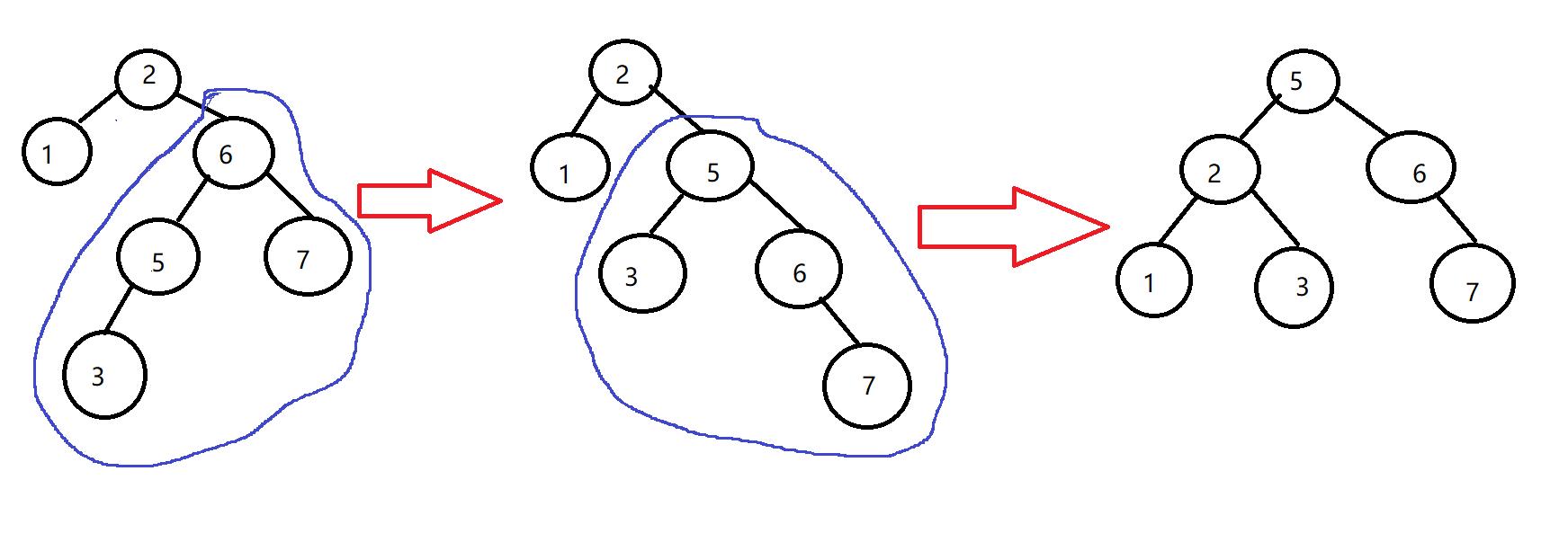
1、如果它的右子树的左子树高度大于它的右子树的右子树的高度
2、先对当前结点的右节点（右子树）进行右旋转
3、再对当前结点进行左旋转的操作即可
情况二：当符合右旋转条件时

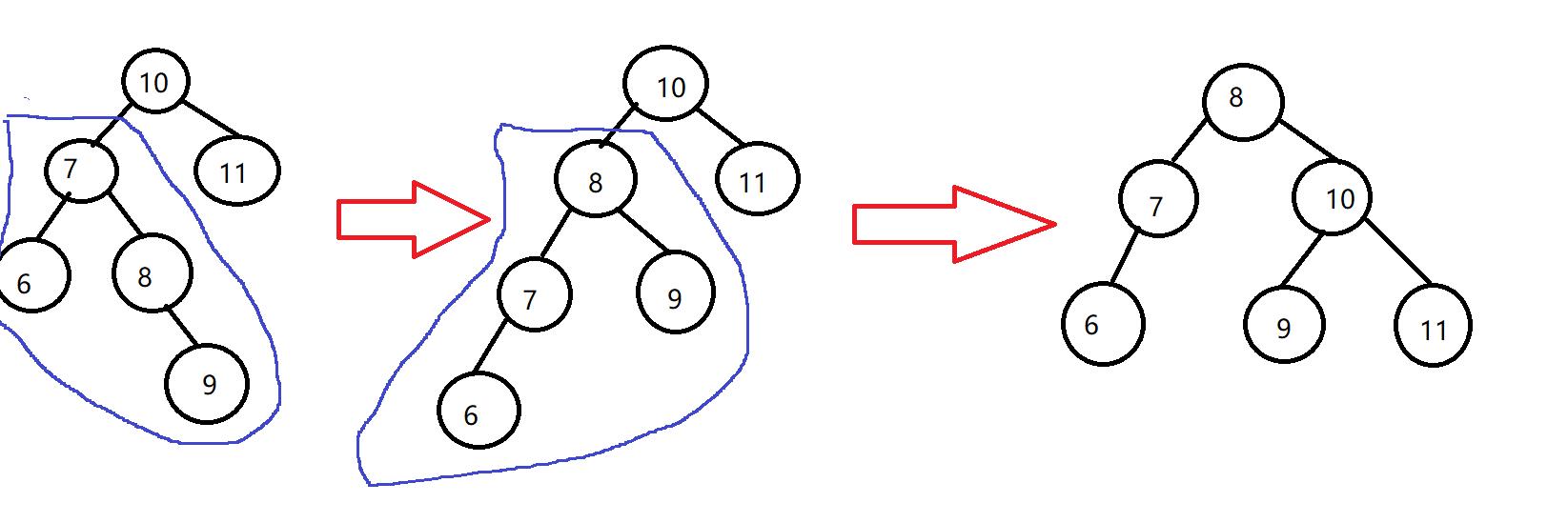
1、如果它的左子树的右子树高度大于它的左子树的左子树的高度
2、先对当前结点的左节点（左子树）进行左旋转
3、再对当前结点进行右旋转的操作即可。

代码实现：

Node类：

package com.Tree.AVL;

public class Node 
    int value;
    Node left;
    Node right;

    public Node() 
    

    public Node(int value) 
        this.value = value;
    

    public int getValue() 
        return value;
    
    //返回左子树的高度
    public int leftHeight() 
        if(left == null) 
            return 0;
         else 
            return left.height();
        
    
    //返回右子树的高度
    public int rightHeight() 
        if(right == null) 
            return 0;
         else 
            return right.height();
        
    
    //返回以该节点为根节点的树的高度
    public int height() 
        return Math.max(left == null ? 0 : left.height(), right == null ? 0 : right.height()) + 1;
    
    //左旋转的方法
    private void leftRotate() 
        //创建一个新节点,值为当前根节点的值
        Node newNode = new Node(value);
        //把新节点的左子树设置为当前节点的左子树
        newNode.left = left;
        //把新节点的右子树设置为当前节点右子树的左子树
        newNode.right = right.left;
        //把当前节点的值替换为右子节点的值
        value = right.value;
        //把当前节点的右子树设置成为当前节点右子树的右子树
        right = right.right;
        //把当前节点的左子树(左子节点)设置为新的节点
        left = newNode;

    
    //右旋转的方法
    private void rightRotate() 
        //创建一个新节点，值为当前根节点的值
        Node newNode = new Node(value);
        //把新节点的右子树设置为当前节点的右子树
        newNode.right = right;
        //把新节点的左子树设置为当前节点左子树的右子树
        newNode.left = left.right;
        //把当前节点的值替换为左子节点的值
        value = left.value;
        //把当前节点的左子树设置成为当前节点左子树的左子树
        left = left.left;
        //把当前节点的右子树(右子节点)设置为新的节点
        right = newNode;
    
    //中序遍历
    public void infixOrder() 
        if(this.left != null) 
            this.left.infixOrder();
        
        System.out.println(this);
        if(this.right != null) 
            this.right.infixOrder();
        
    
    //添加节点
    public void add(Node node) 
        if(node ==null) 
            return;
        
        if(node.value < this.value) 
            //如果当前结点的左子节点为null，则将node添加到当前结点的左子节点上
            if(this.left == null) 
                this.left = node;
             else  //递归向左子树添加
                this.left.add(node);
            
         else  //传入结点的值大于等于当前子树的根节点的值
            if(this.right == null) 
                this.right = node;
             else  //递归向右子树添加
                this.right.add(node);
            
        
        //当添加完一个节点后，如果右子树的高度-左子树的高度大于1，左旋转
        if(rightHeight() - leftHeight() > 1) 
            //如果他的右子树的左子树的高度大于它的右子树的右子树的高度
            if(right != null && right.leftHeight() > right.rightHeight()) 
                //先对当前节点的右节点(右子树)进行右旋转
                right.rightRotate();
                //然后再对当前节点进行左旋转
                leftRotate();
             else 
                //直接进行左旋转即可
                leftRotate();
            
            return;
        
        //当添加完一个节点后，如果左子树的高度-右子树的高度大于1，右旋转
        if(leftHeight() - rightHeight() > 1) 
            //如果它的左子树的右子树高度大于它的左子树的左子树的高度
            if(left != null && left.rightHeight() > left.leftHeight()) 
                //先对当前节点的左节点(左子树)进行左旋转
                left.leftRotate();
                //再对当前节点进行右旋转
                rightRotate();
             else 
                //直接进行右旋转即可
                rightRotate();
            
        
    

    @Override
    public String toString() 
        return "Node" +
                "value=" + value +
                '';
    

AVLTree类：

package com.Tree.AVL;


public class AVLTree 
    Node root;

    //添加节点
    public void add(Node node) 
        if(root == null) 
            root = node;
         else 
            root.add(node);
        
    
    //中序遍历
    public void infixOrder() 
        if(root != null) 
            root.infixOrder();
         else 
            System.out.println("null");
        
    

测试类：

package com.Tree.AVL;

public class AVLTreeDemo 
    public static void main(String[] args) 
        int[] arr = 2,1,6,5,7,3;
        AVLTree avl = new AVLTree();
        for (int i = 0; i < arr.length; i++) 
            avl.add(new Node(arr[i]));
        
        avl.infixOrder();
        System.out.println(avl.root.height());
        System.out.println(avl.root.leftHeight());
        System.out.println(avl.root.rightHeight());
    

二叉排序树的运行结果：

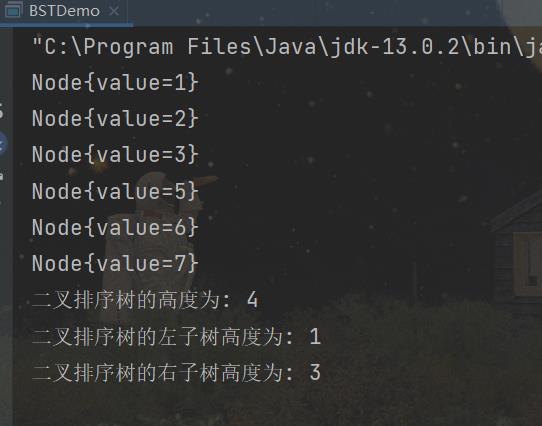
AVL树的运行结果：

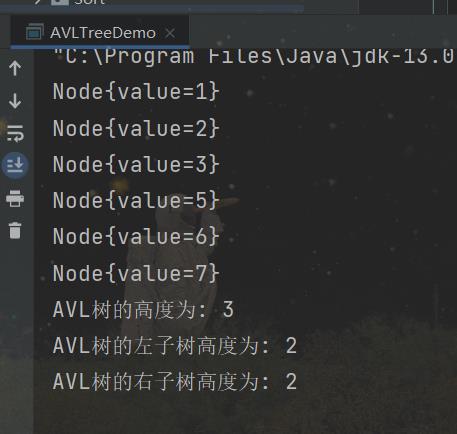
从以上两个运行结果可以看出：树的高度、树的左、右子树高度经过处理后，原来的二叉排序树变为了一棵AVL树。