翻译: 最小二乘法 - 交互式线性代数

Posted 2021-12-29 AI架构师易筋

1. 目标

1. 学习最佳拟合问题的示例。
2. 学习将最佳拟合问题转化为最小二乘问题。
3. 秘诀：找到最小二乘解（两种方法）。
4. 图片：最小二乘解的几何。
5. 词汇： 最小二乘解。

在本节中，我们将回答以下重要问题：

假设 Ax =b 没有解决方案。最好的近似解是什么？

出于我们的目的，最佳近似解称为最小二乘解。我们将介绍两种寻找最小二乘解的方法，并将给出几种最佳拟合问题的应用。

2. 最小二乘解

我们首先明确我们对不一致矩阵方程的“最佳近似解”的含义Ax =b

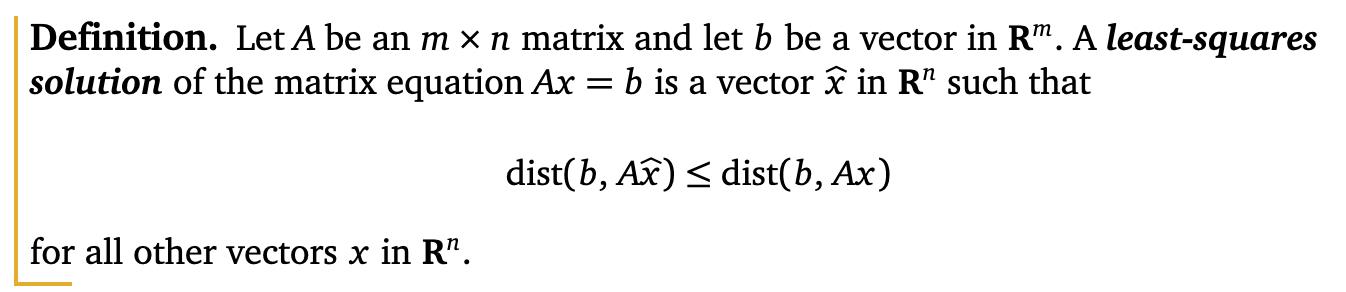
回想起那个 dist(v, w) = ||v - w|| 是向量v和w之间的距离。 “最小二乘法”一词源于这样一个事实：

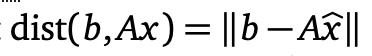
是向量项的平方和的平方根
所以最小二乘法最小化了条目之间差异的平方和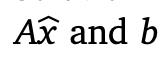
换句话说，最小二乘解解方程 Ax = b 尽可能接近，因为差的平方和 b − Ax 被最小化。











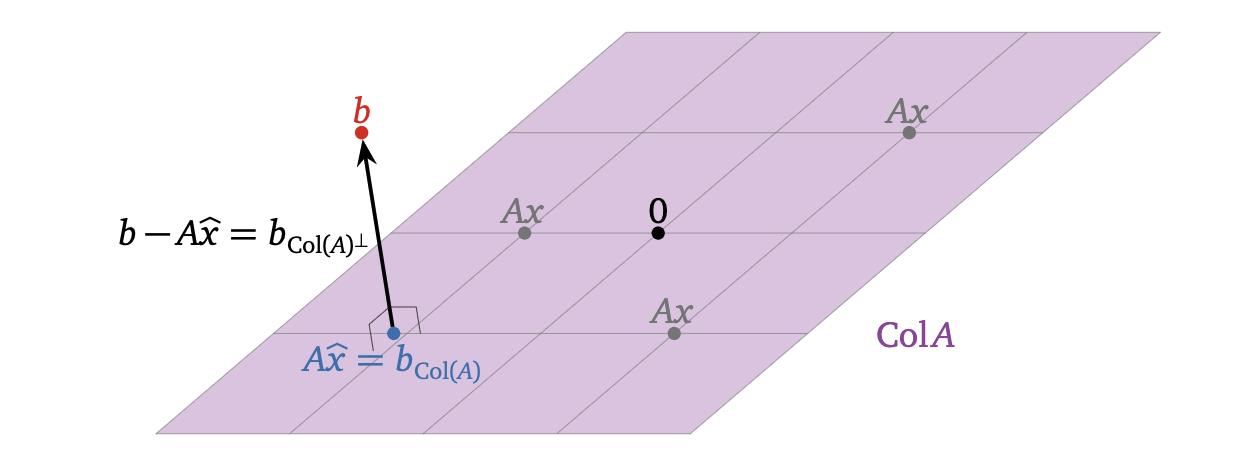
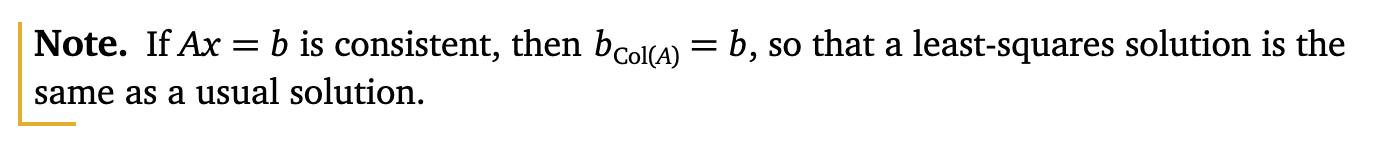
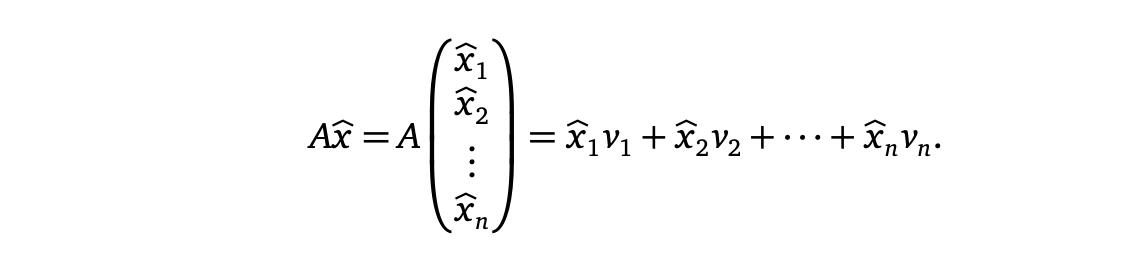
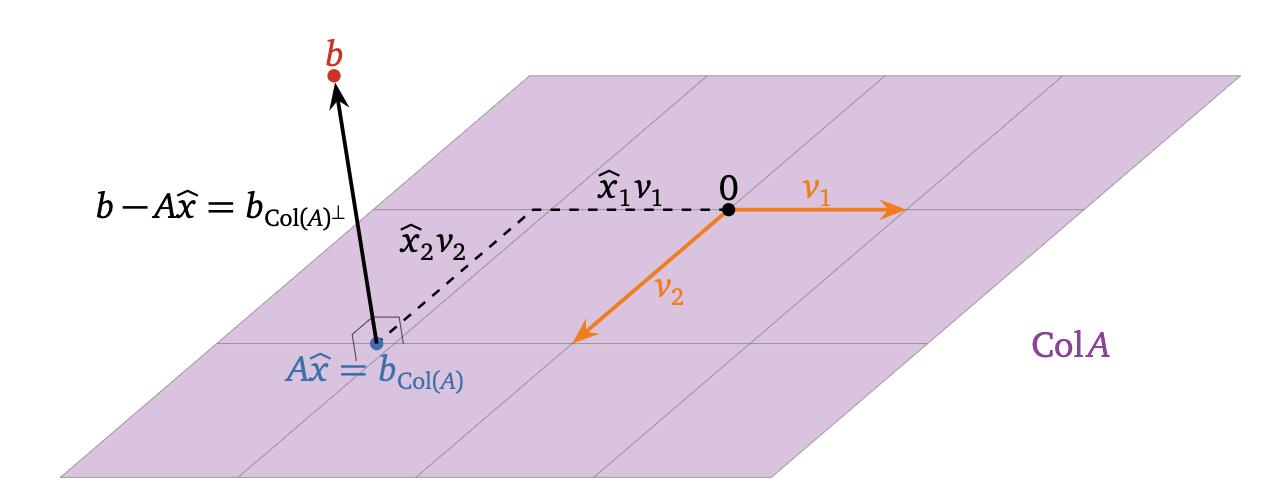
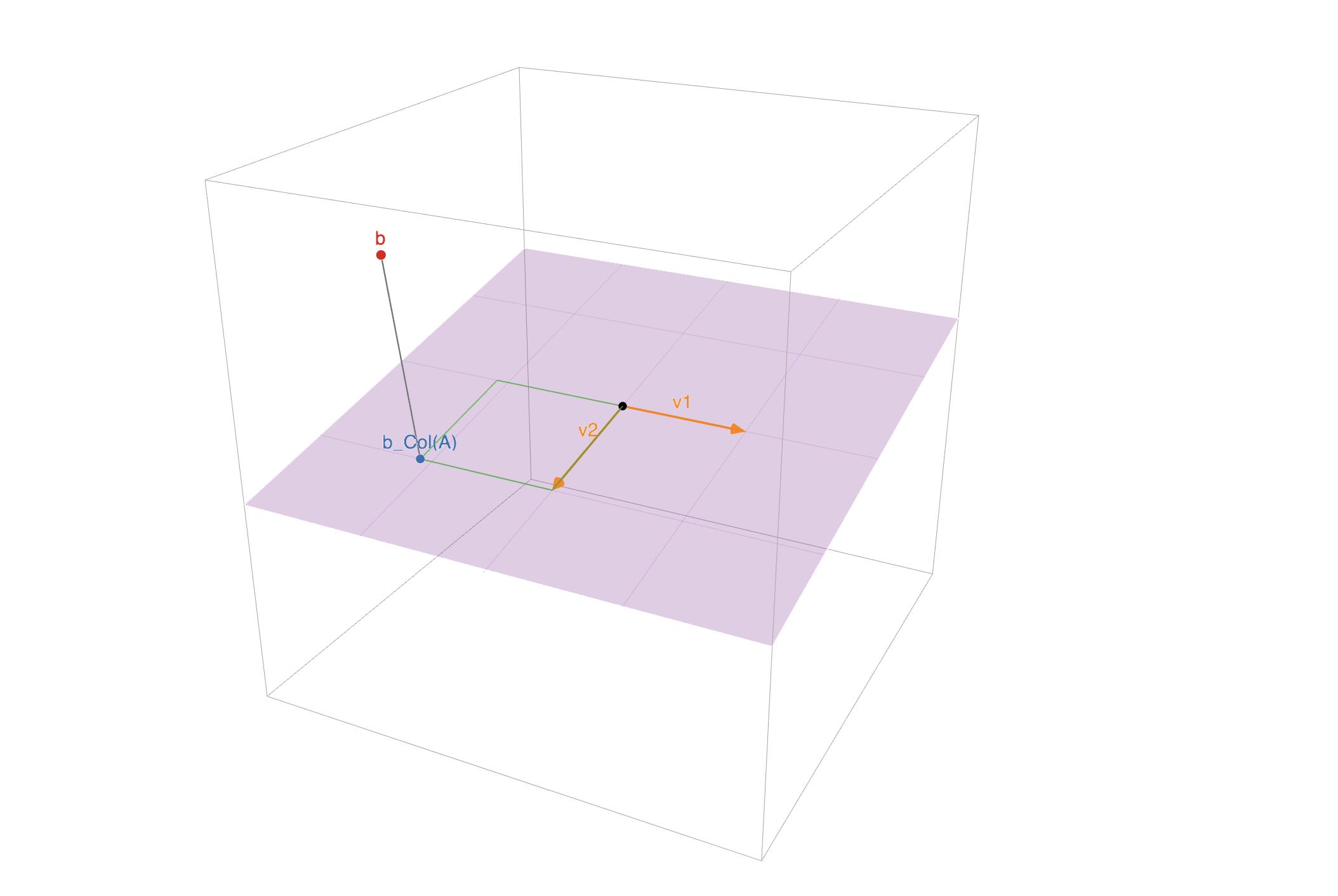
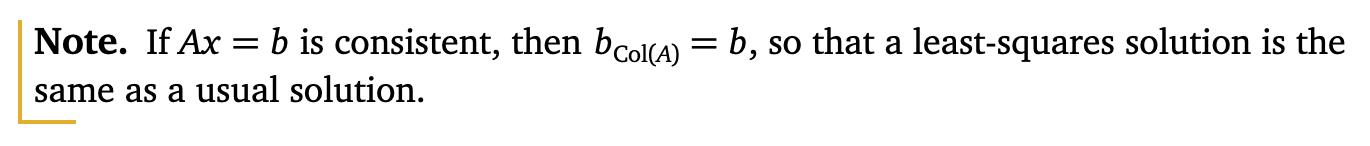
我们在第 6.3 节中学会了解决这种正交投影问题。


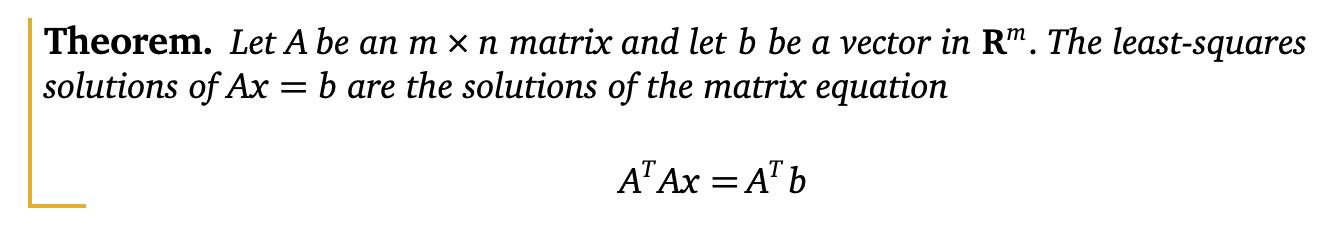
特别是，找到最小二乘解意味着求解一致的线性方程组。我们可以将上述定理转化为一个秘诀：


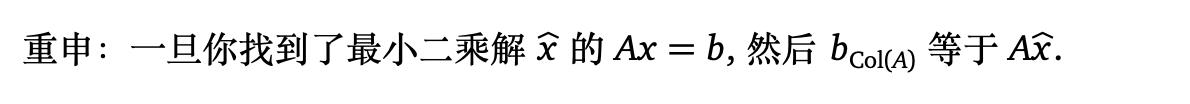
读者可能已经注意到，我们小心翼翼地用复数表示“最小二乘解”，而用不定冠词表示“最小二乘解”。这是因为最小二乘解不需要唯一：实际上，如果A 是线性相关的，那么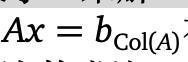有无穷多个解。以下定理给出了唯一性的等效标准，是中该的类比。


像往常一样，在存在正交集的情况下，涉及投影的计算变得更容易。确实，如果A是一个 m×n具有正交列的矩阵
u1,u2,...,um 那么我们可以用的来写

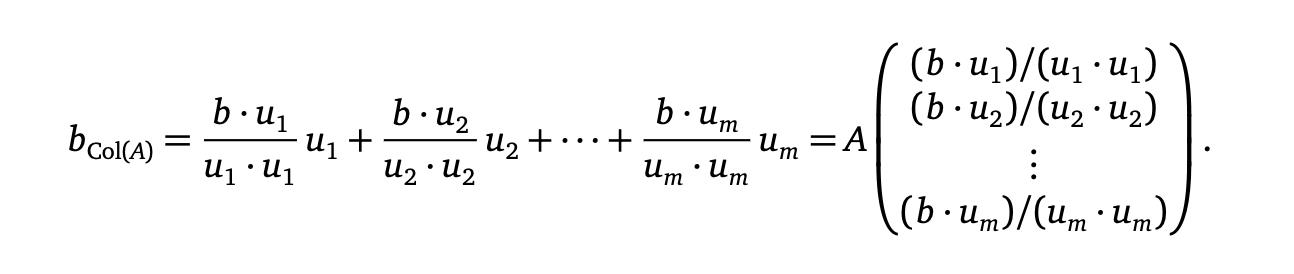
请注意，在这种情况下，最小二乘解是唯一的，因为。

这个公式在科学中特别有用，因为具有正交列的矩阵在自然界中经常出现。

3. 最佳拟合问题

在本小节中，我们将给出最小二乘法在数据建模中的应用。我们从一个基本的例子开始。
示例（最佳拟合线） 假设我们测量了三个数据点(0, 6), (1, 0), (2, 0).
并且我们的这些数据模型断言这些点应该位于一条线上。当然，这三个点实际上并不位于一条线上，但这可能是由于我们的测量错误造成的。我们如何预测他们应该躺在哪条线上？

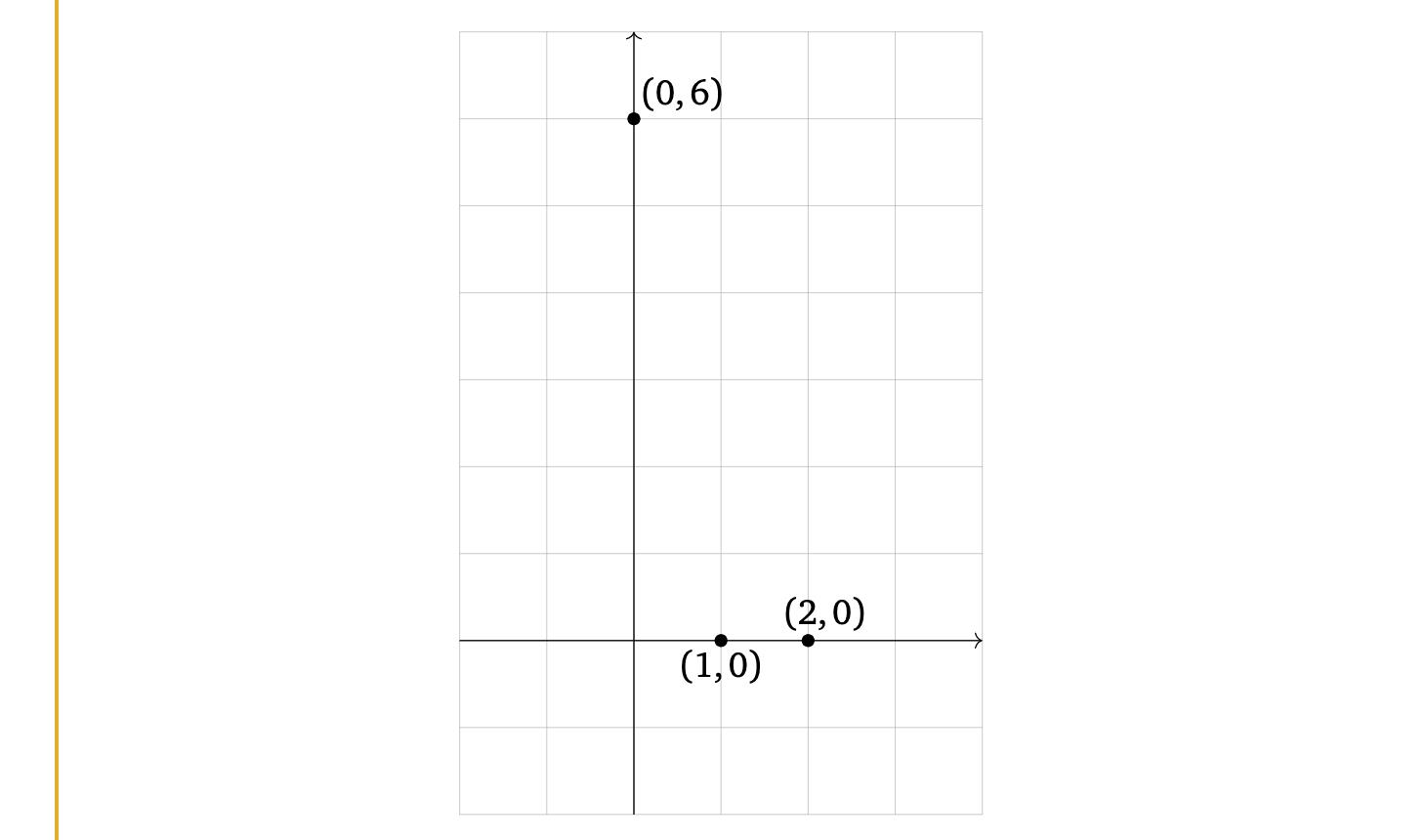
（非垂直）线的一般方程是 y = Mx + B
如果我们的三个数据点位于这条线上，那么将满足以下等式：

为了找到最佳拟合线，我们尝试在未知数中求解上述方程 M 和 B.
由于三个点实际上并不位于一条线上，因此没有实际解，因此我们计算最小二乘解。

把我们的线性方程变成矩阵形式，我们试图解决 Ax=b 为了

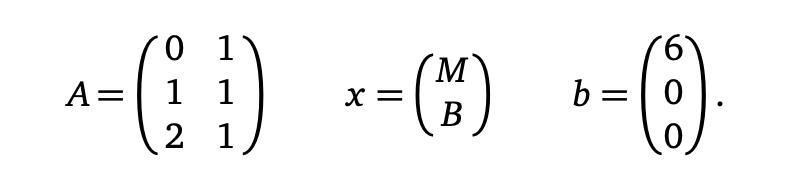
我们在这个解决了这个最小二乘问题：唯一的最小二乘解 Ax=b是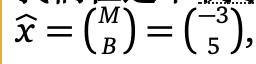所以最合适的线是





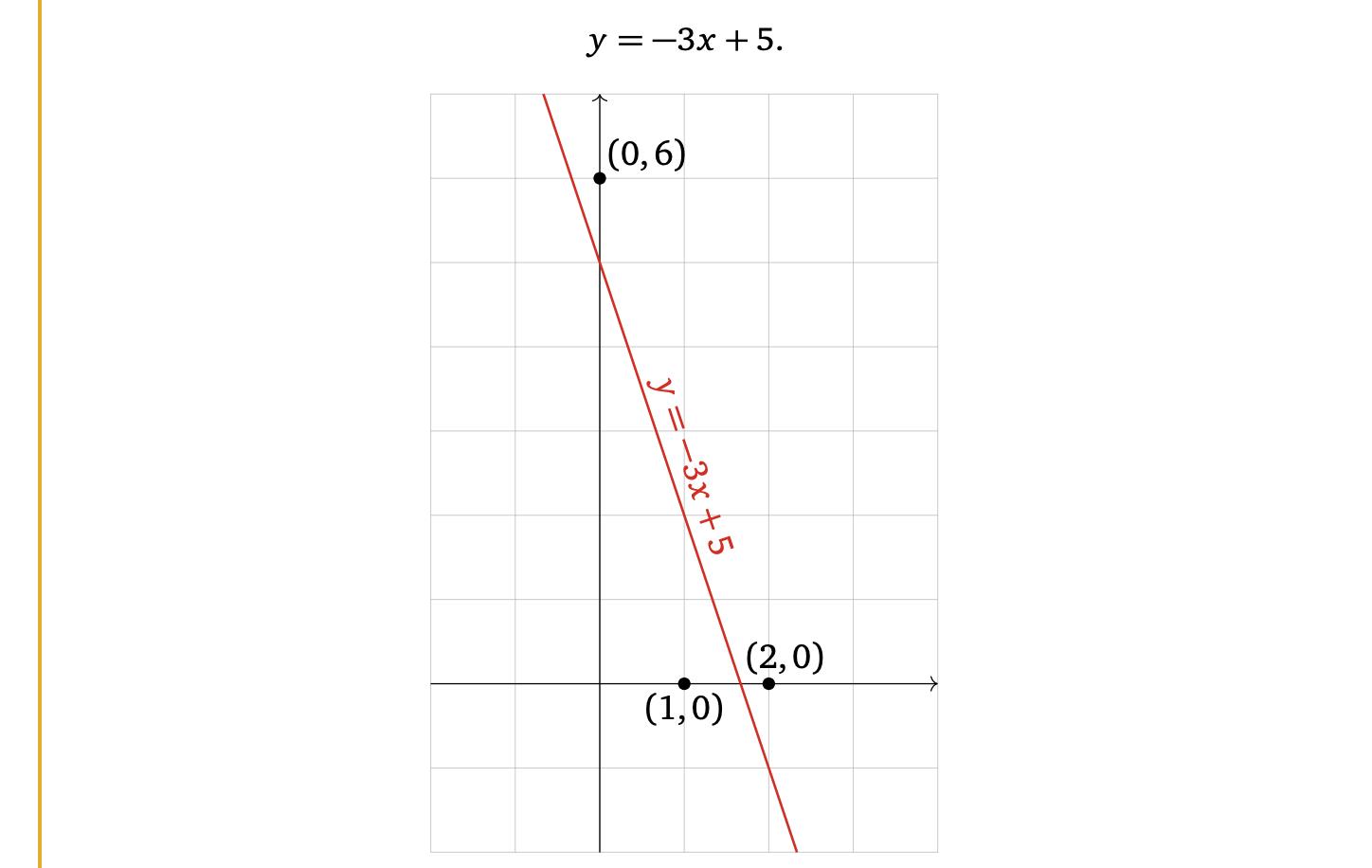
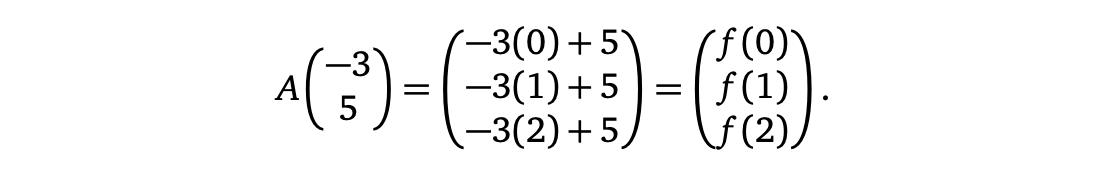
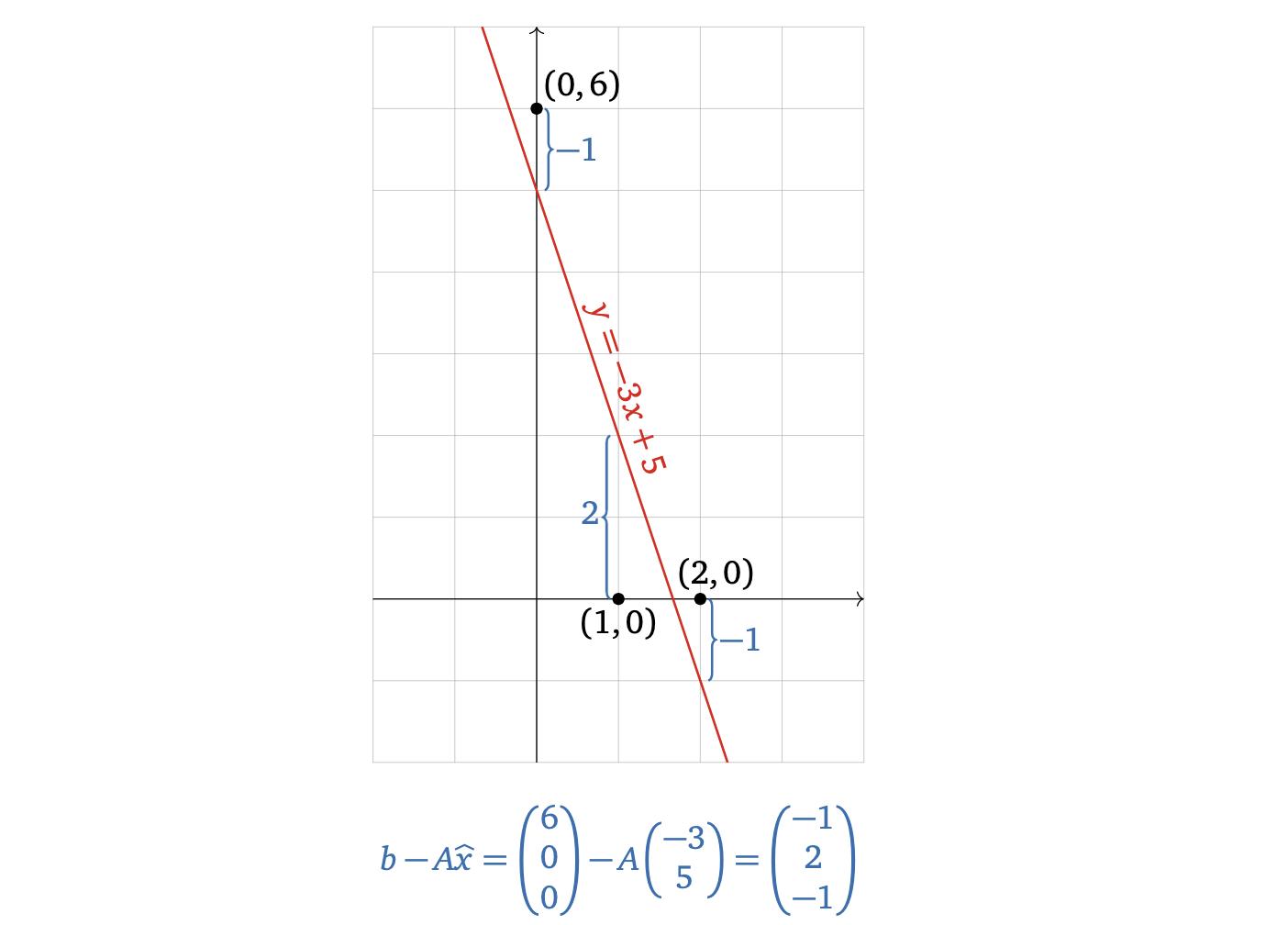
最佳拟合线最小化这些垂直距离的平方和。

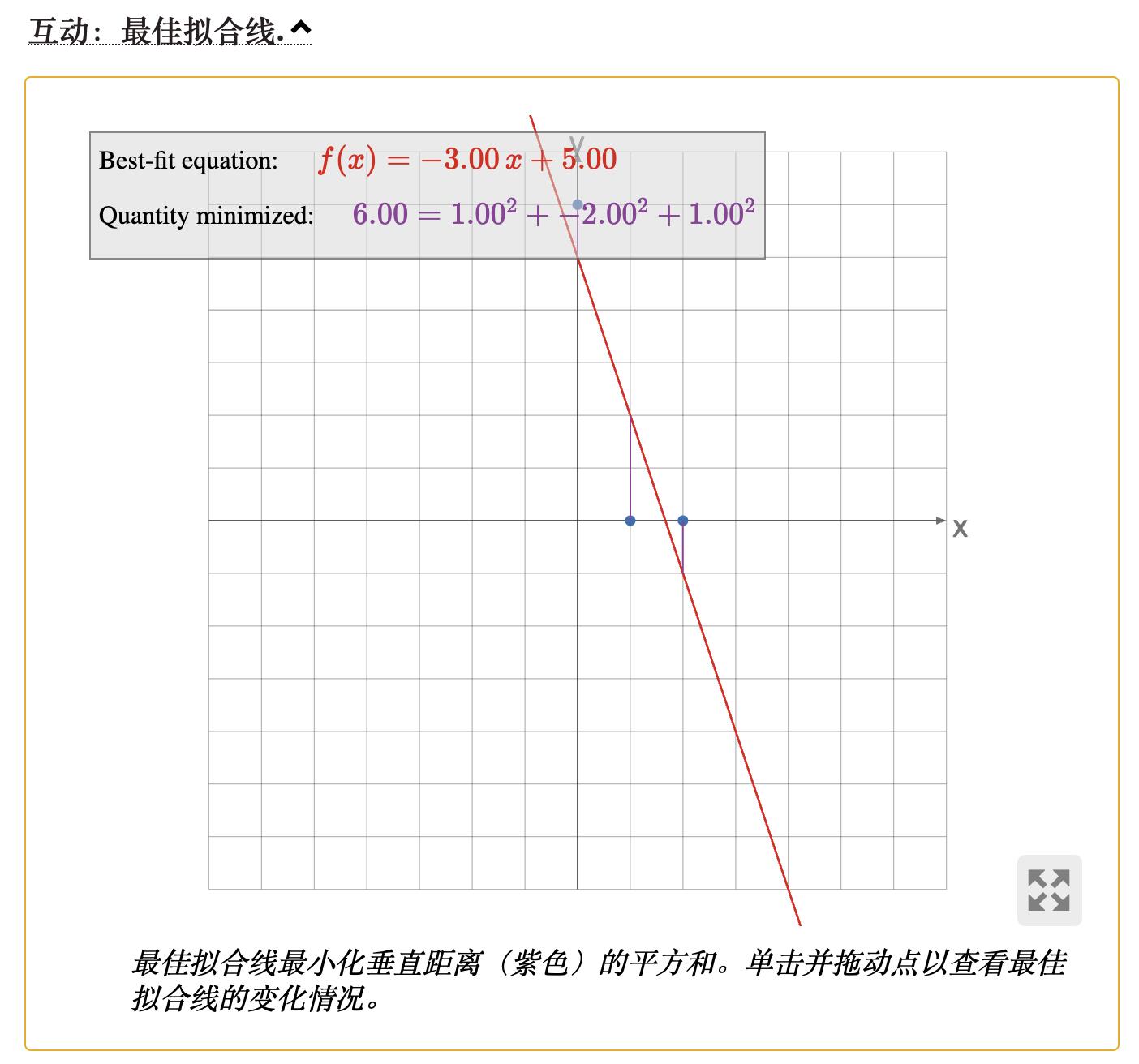
以上所有示例都具有以下形式：一定数量的数据点(x, y) 被指定，我们想找到一个函数

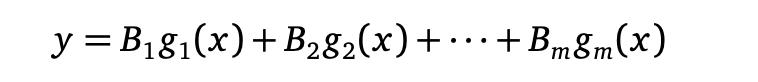
强调功能的性质 gi 真的无关紧要，请考虑以下示例。

高斯发明了最小二乘法来找到最合适的椭圆：他正确预测了小行星谷神星在 1801 年从太阳后面经过时的（椭圆）轨道。

参考

https://textbooks.math.gatech.edu/ila/least-squares.html