归并排序 (递归 && 非递归)

Posted 2021-12-29 跳动的bit

一、递归版本

🔑 核心思想 🔑

  归并排序 (MERGE-SORT) 是建立在归并操作上的一种有效的排序算法，该算法是采用分治法 (Divide and Conquer) 的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列有序。若将两个有序表合并成一个有序表，称为二路归并。

  归并排序核心步骤：

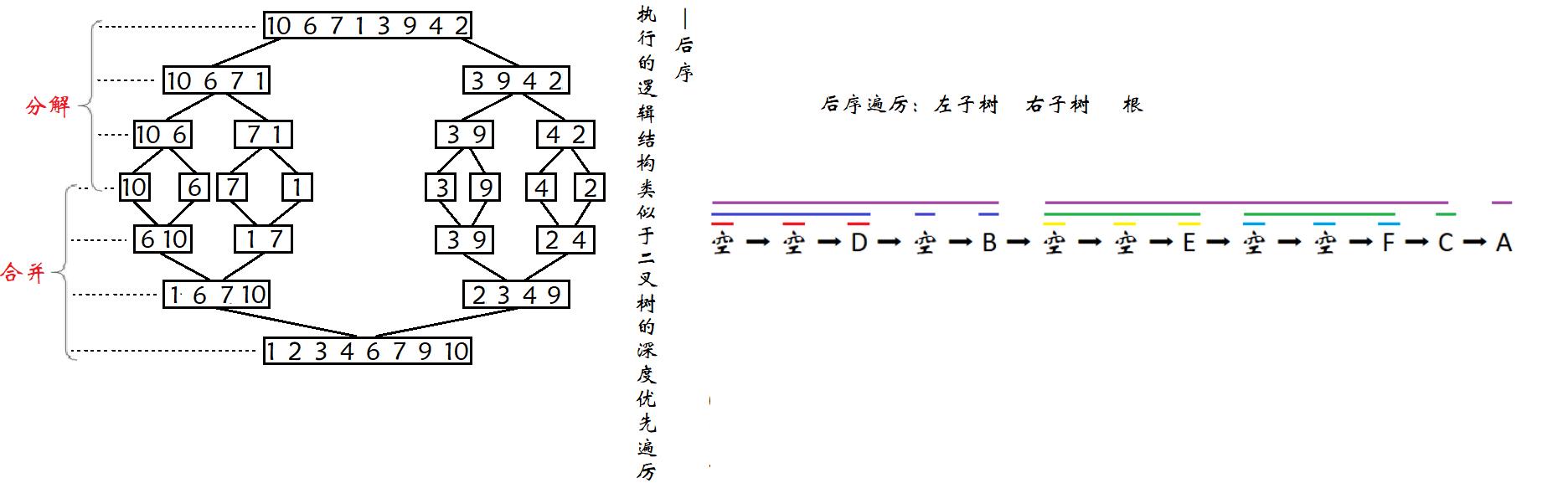
❗ 动图演示：❕

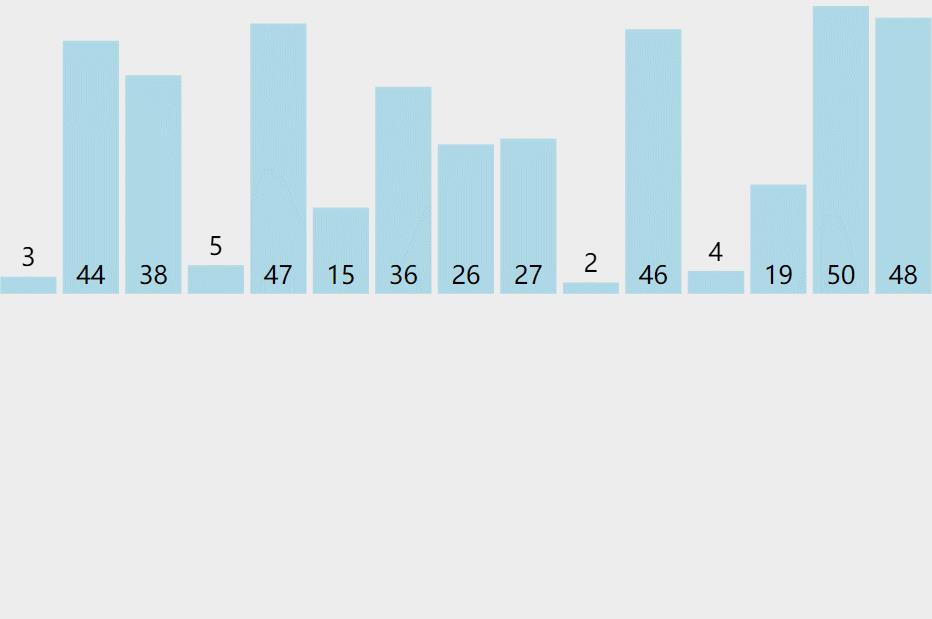
🧿 实现代码 —— 递归版 ：

void _MergeSort(int* a, int left, int right, int* temp)

	//只有一个值
	if (left >= right)
		return;

	//[left, mid][mid+1, right]
	int mid = (right + left) / 2;

	//递归
	_MergeSort(a, left, mid, temp);
	_MergeSort(a, mid + 1, right, temp);

	//归并到temp
	int begin1 = left, end1 = mid;
	int begin2 = mid + 1, end2 = right;
	
		//&&其中一段区间结束就结束了
	int index = left;
	while (begin1 <= end1 && begin2 <= end2)
	
		if (a[begin1] < a[begin2])
		
			temp[index++] = a[begin1++];
		
		else
		
			temp[index++] = a[begin2++];
		
	
		//begin2结束了，拷贝剩下的begin1
	while (begin1 <= end1)
	
		temp[index++] = a[begin1++];
	
		//begin1结束了，拷贝剩下的begin2
	while (begin2 <= end2)
	
		temp[index++] = a[begin2++];
	
		//归并后的结果，拷贝至原数组
	int i = 0;
	for (i = left; i <= right; i++)
	
		a[i] = temp[i];
	

void MergeSort(int* a, int n)

	//临时数组 
	int* temp = (int*)malloc(sizeof(int) * n);
	//子函数递归
	_MergeSort(a, 0, n - 1, temp);
	//释放临时数组
	free(temp);

二、非递归版本

🧿 实现代码 —— 非递归版 ：

🔑 核心思想 🔑

void MergeSortNonR(int* a, int n)

	//临时数组 
	int* temp = (int*)malloc(sizeof(int) * n);
	int groupNum = 1;
	int i = 0; 
	while (groupNum < n)
	
		for (i = 0; i < n; i += 2 * groupNum)
		
			//[begin1, end1][begin2, end2]
			int begin1 = i, end1 = i + groupNum - 1;
			int begin2 = i + groupNum, end2 = i + groupNum * 2 - 1;
			//归并
			int index = begin1;
			//数组的数据个数，并不一定是按整数倍，所以分组可能越界或不存在
				//1.[begin2,end2]不存在或越界，修正为一个不存在的区间
			if (begin2 >= n)
			
				begin2 = n + 1;
				end2 = n;
			
				//2.end1越界，修正后归并
			if (end1 >= n)
			
				end1 = n - 1;
			
				//3.end2越界，修正后归并
			if (end2 >= n)
			
				end2 = n - 1;
			
			while (begin1 <= end1 && begin2 <= end2)
			
				if (a[begin1] < a[begin2])
				
					temp[index++] = a[begin1++];
				
				else
				
					temp[index++] = a[begin2++];
				
			
			//begin2结束了，拷贝剩下的begin1
			while (begin1 <= end1)
			
				temp[index++] = a[begin1++];
			
			//begin1结束了，拷贝剩下的begin2
			while (begin2 <= end2)
			
				temp[index++] = a[begin2++];
			
		
		//拷贝回原数组
		for (i = 0; i < n; i++)
		
			a[i] = temp[i];
		
		//迭代
		groupNum *= 2;

		//输出每层
		//PrintArray(a, n);

	
	//释放临时数组
	free(temp);

❗ 归并排序的特性总结：❕

  1️⃣ 归并的缺点在于需要O(N)的空间复杂度，归并排序的思考更多的是解决在磁盘中的外排序问题

  2️⃣ 时间复杂度：O(N*logN)

  3️⃣ 空间复杂度：O(N)

  4️⃣ 稳定性：稳定