随机过程 1 - 相关与随机过程
Posted Ciaran-byte
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了随机过程 1 - 相关与随机过程相关的知识,希望对你有一定的参考价值。
相关与随机过程
1. 相关的直观表示
1.1 多维随机变量的联合概率密度与联合分布
随机过程中最重要的概念就是相关。假设我们有两个随机变量X和Y
Joint Distribution f X , Y ( x , y ) = ∂ 2 ∂ x ∂ y F X , Y ( x , y ) F X , Y ( x , y ) = P ( Z ≤ x , Y ≤ y ) \\textJoint Distribution \\\\ f_X,Y (x,y) = \\frac\\partial^2\\partial_x \\partial_y F_X,Y(x,y) \\\\ F_X,Y(x,y) = P(Z \\leq x,Y \\leq y) Joint DistributionfX,Y(x,y)=∂x∂y∂2FX,Y(x,y)FX,Y(x,y)=P(Z≤x,Y≤y)
多维随机变量联合概率密度就是联合分布函数的导数
1.2 两个随机变量的相关
下面,我们想举几个例子,直观的表示两个随机变量之间的联系
1.2.1 Independent
Independent \\textIndependent Independent
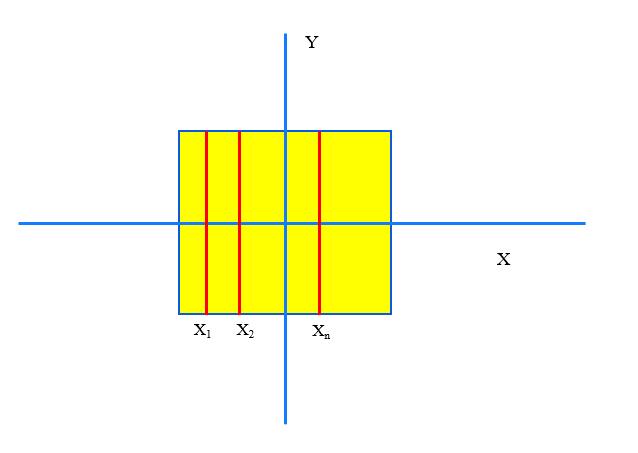
f X , Y ( x , y ) = 1 4 ∣ x ∣ ≤ 1 , ∣ y ∣ ≤ 1 0 o t h e r s f_X,Y(x,y)= \\begincases \\frac14 & |x| \\leq 1, |y| \\leq 1 \\\\ 0 & others \\endcases fX,Y(x,y)=410∣x∣≤1,∣y∣≤1others
如果我们想要求XY的联合概率密度,其实就等于X和Y各自的概率密度的乘积
f X , Y ( x , y ) = f X ( x ) f Y ( y ) f_X,Y(x,y) = f_X(x) f_Y(y) fX,Y(x,y)=fX(x)fY(y)
X和Y是独立的,从图中也可以看出来,X改变的时候,Y的分布不会受到影响
X从x1到x2到xn,Y的分布都是一样的
1.2.2 Correlated
Correlated \\textCorrelated Correlated
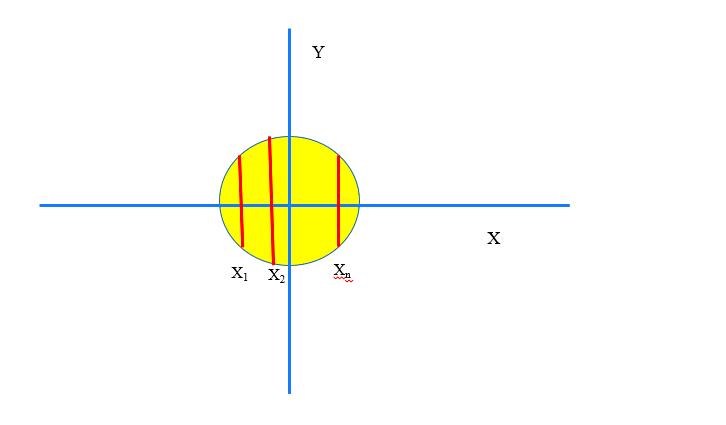
f X , Y ( x , y ) = 1 π x 2 + y 2 ≤ 1 0 o t h e r s f_X,Y(x,y)= \\begincases \\frac1\\pi & x^2 + y^2 \\leq 1 \\\\ 0 & others \\endcases fX,Y(x,y)=π10x2+y2≤1others
f X , Y ( x , y ) = f X ( x ) f Y ( y ) f_X,Y(x,y) \\cancel = f_X(x) f_Y(y) fX,Y(x,y)= fX(x)fY(y)
当X和Y的相关关系从矩形区域变成了圆形区域,X和Y就有了相关关系,X取不同的值的时候Y的分布会发生变化
现在,虽然X和Y有了相关关系,但是他们之间没有非常明显的相关趋势
1.2.3 Linear Correlation
Linear Correlation \\textLinear Correlation Linear Correlation
f X , Y ( x , y ) = 1 ∣ Ω ∣ ( x , y ) ≤ Ω 0 o t h e r s f_X,Y(x,y)= \\begincases \\frac1|\\Omega| & (x,y) \\leq \\Omega \\\\ 0 & others \\endcases fX,Y(x,y)=∣Ω∣10(x,y)≤Ωothers
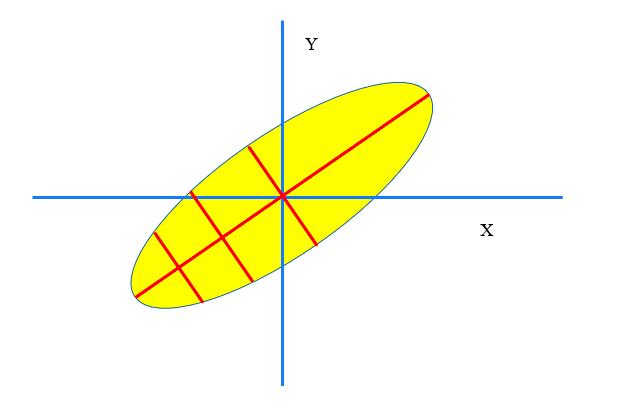
当X和Y的相关关系从圆形区域变成纺锤形,现在我们发现,X的变化会引起Y的变化。并且这种变化非常有规律。随着X的增大,Y的均值随之增大。此时X和Y产生了线性的关联
X和Y是线性关联,但又不是完全的线性。因为纺锤形是有宽度的,Y并不是随着X的增大而严格增大。这个线性度我们是有表征方法的。
相关系数描述的就是这个纺锤形的胖瘦。相关系数越大,纺锤形越瘦。说明X和Y的线性度越高。如果线性度达到极限,就是一条线,也就变成了严格的线性相关。
2. 随机变量的线性相关
2.1 线性相关的求解及其含义
在相关关系中,我们应该重点关注的是线性相关问题
Y = α Z ⇒ E ( Y − α Z ) 2 Mean Square Error ⇒ m i n α E ( Y − α Z ) 2 ⇒ α o p t = E ( Z Y ) E ( Z 2 ) Y = \\alpha Z \\Rightarrow E(Y - \\alpha Z)^2 \\quad \\textMean Square Error \\\\ \\Rightarrow min_\\alpha E(Y - \\alpha Z)^2 \\Rightarrow \\alpha_opt = \\fracE(ZY)E(Z^2) Y=αZ⇒E(Y−αZ)2Mean Square Error⇒minαE(Y−αZ)2⇒αopt=E(Z2)E(ZY)
假设我们有两个随机变量Y和Z,我们希望计算Z和Y的相关关系,如果直接进行线性相关计算,多半是不行的,会有误差。
因此,我们会引入均方误差的概念,去表征线性估计的误差。以均方误差最小为优化目标,最终得到的系数实际上就是互相关与自相关相除。
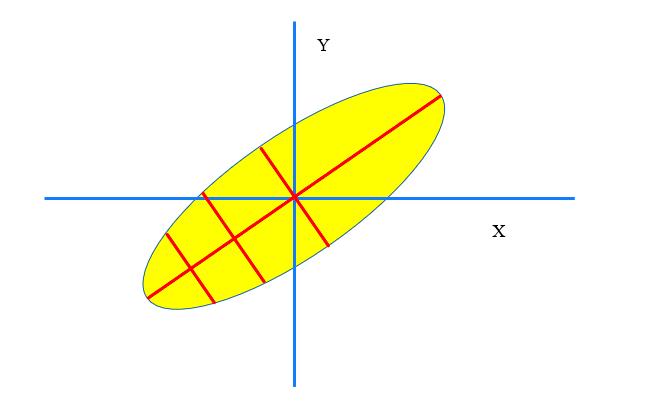
如果Z和Y是严格的线性相关,均方误差必然是0。如果不是严格的相关,均方误差就不是0,并且反应在图像上就是纺锤形的宽度。
而α的大小,反应在纺锤形上,就是斜率。这个纺锤形的长轴,就是最小均方误差意义下的线性估计。
2.2 相关的符号表示说明
相关就是两个随机变量乘在一起求期望
Correlation E ( Z Y ) \\textCorrelation \\\\ E(ZY) CorrelationE(ZY)
不过我们看到的相关,可能会有另外一种表示
E ( ( Z − E ( Z ) ) ( Y − E ( Y ) ) E((Z-E(Z))(Y-E(Y)) E((Z−E(Z))(Y−E(Y))
这种写法实际上是对相关做了中心化以后的结果
E ( ( Z − E ( Z ) ) ( Y − E ( Y ) ) = E ( Z Y ) − E ( E ( Z ) Y ) − E ( Z E ( Y ) ) + E ( Z ) E ( Y ) E((Z-E(Z))(Y-E(Y)) = E(ZY) - E(E(Z)Y)-E(ZE(Y)) + E(Z)E(Y) E((Z−E(Z))(Y−E(Y))=E(ZY)−E(E(Z)Y)−E(ZE(Y))+E(Z)E(Y)
没有随机性的东西可以放到相关外面,继续可以得到
E
(
(
Z
−
E
(
Z
)
)
(
Y
−
E
(
Y
)
)
=
E
(
Z
Y
)
−
E
(
Z
)
E
(
Y
)
−
E
(
Z
)
E
以上是关于随机过程 1 - 相关与随机过程的主要内容,如果未能解决你的问题,请参考以下文章