随机过程 6 - 多元相关

Posted 2021-12-29 Ciaran-byte

多元相关

文章目录

• 多元相关
• • 1. 概述
  • 2. 三个角度看待相关矩阵
  • • 2.1 白化
    • 2.2 PCA
    • • 2.2.1 原理
      • 2.2.2 PCA与去相关
      • 2.2.3 PCA几何图形影响因素
    • 2.3 展开
    • • 2.3.1 随机矢量的KL展开
      • 2.3.2 随机过程的KL展开
      • 2.3.3 周期性宽平稳随机过程的KL展开
      • 2.3.4 非周期性宽平稳随机过程的KL展开--谱表示

1. 概述

  相关是研究随机过程的重要工具。之前，我们研究的都是两个随机变量的相关性。现在我们想扩展到随机矢量的相关性。对多元相关问题研究的角度有两个，一个是从分布的角度来看的，另一个是从直观的角度来看的。

$$\begin{gathered} Z,Y\Rightarrow E(ZY) \\ Z=(Z_1,...,Z_n{)}^T \\ \to \text{Distribution} \\ \to \text{Intuitive} \end{gathered}$$

  事实上，从分布的角度来表示相关并不容易，因为相互之间的作用可能会非常复杂。

  我们就在二维空间上用等高线的形式，去描述两个随机变量的关系

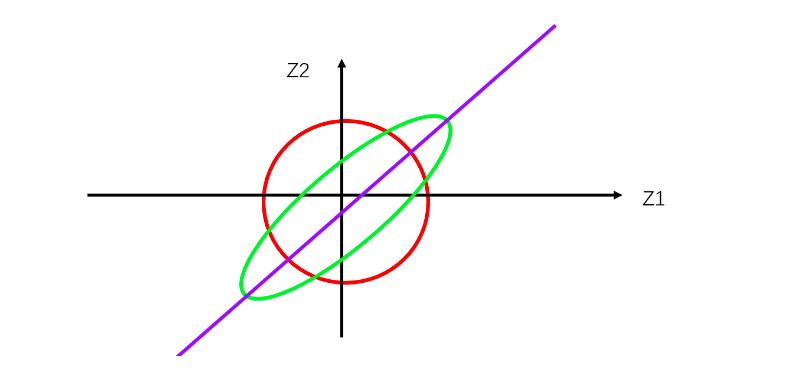
• 如果两个随机变量的等高线是个圆，那么这个两个随机变量不独立，但是没有明显的相关性
• 如果两个随机变量的等高线是个椭圆，那么这个两个随机变量不独立，并且具有明显的相关性
• 如果两个随机变量的等高线是条直线，那么两个随机变量是不独立的，并且二者之间具有强相关性

  如果是更高维度的分布函数，就很难统计了。我们希望使用更加直观的方法去描述多元随机变量之间的相关关系。

  事实上，我们可以用更加简单的方法，通过相关矩阵的方法去描述多元相关问题

$$\begin{gathered} E(Z_i{Z}_j)E(Z_i^2) \\ (1\le i<j\le n)\Rightarrow C_n^2=\frac{n(n+1)}{2} \end{gathered}$$

  除了自相关以外，还有n(n+1)/2种的互相关

  我们相关矩阵得到的描述是这样的

$$\begin{gathered} \text{Correlation Matrix} \\ E(Z{Z}^T)=\left(\begin{array}{ccccc}E(Z_1^2)& E(Z_1{Z}_2)& ...& E(Z_1{Z}_n)& \\ E(Z_2{Z}_1)& E(Z_2^2)& ...& E(Z_2{Z}_n)& \\ ...& ...& ...& ...& \\ E(Z_n{Z}_1)& E(Z_n{Z}_2)& ...& E(Z_n^2)& \end{array}\right) \end{gathered}$$

  相关矩阵具有这样的性质

• 对称
• 正定

  下面，我们将基于相关矩阵，从三个不同的角度去看待相关矩阵

• 白化
• PCA
• KL展开

2. 三个角度看待相关矩阵

2.1 白化

  首先第一个角度，是去相关化的角度，我们知道，我们的随机变量之间一般都是有相关性的，但是，如果我们通过某种线性变换，然后随机变量之间的相关性可以被去掉，这个动作就叫白化，也叫做去相关性

$$\text{Decorrelation }\text{ (Whiten) }$$

$$\begin{gathered} \exists AY=AZ \\ Z\in {\mathbb{R}}^{n}A\in {\mathbb{R}}^{n\ast n} \end{gathered}$$

  经过白化处理得到的相关矩阵Y应该是个对角阵

$$E(Y{Y}^H)=diag({\lambda }_1,....,{\lambda }_n)$$

  事实上，求解A矩阵是个不适定的问题。因为未知数有n*n个，但是方程只有
n(n-1)/2个。但是我们有一些先验知识。

  我们表示一下Y的相关矩阵

$$R_Y=E(Y{Y}^T)=E(AZ{Z}^T{A}^T)=AE(Z{Z}^T)A^T=A{R}_Z{A}^T$$

  我们知道相关矩阵R_Z是对称的，一定可以做谱分解(特征分解)

$$R_Z=\sum _{k=1}^n{\lambda }_k{u}_k{u}_{随机过程\; 6\; -\; 多元相关}$$

随机过程8 - 多元高斯分布及其线性性质

随机过程8 - 多元高斯分布及其线性性质

随机过程8 - 多元高斯分布及其线性性质

机器学习之概率与统计- 多元随机变量及其分布

WinBUGS对多元随机波动率模型：贝叶斯估计与模型比较