ybtoj 二分进阶DPC. 3.攻击法坛

Posted 2021-12-29 SSL_ZZL

C. 3.攻击法坛

• 题面
• 解题思路
• Code

ybtoj 二分进阶 C. 3.攻击法坛

---

题面

---

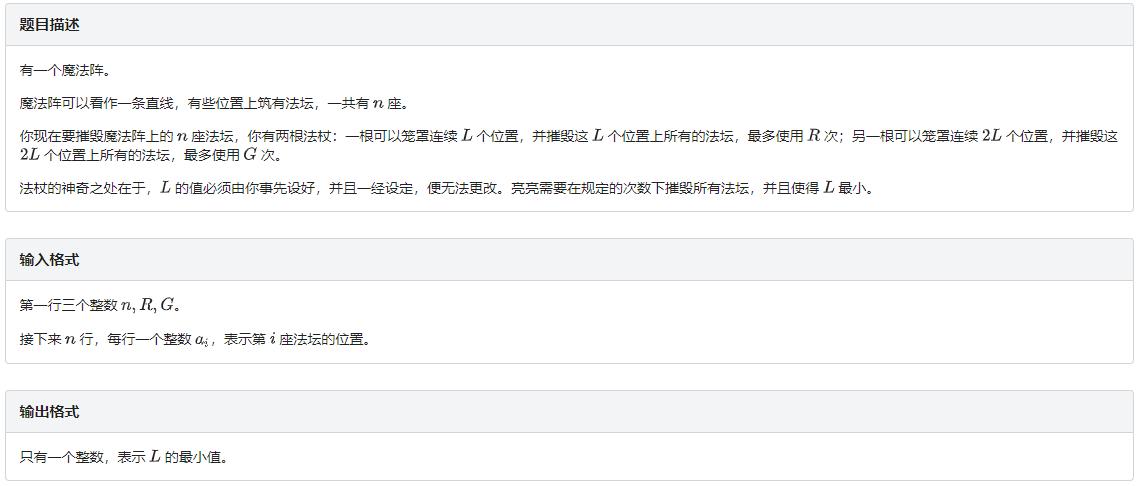
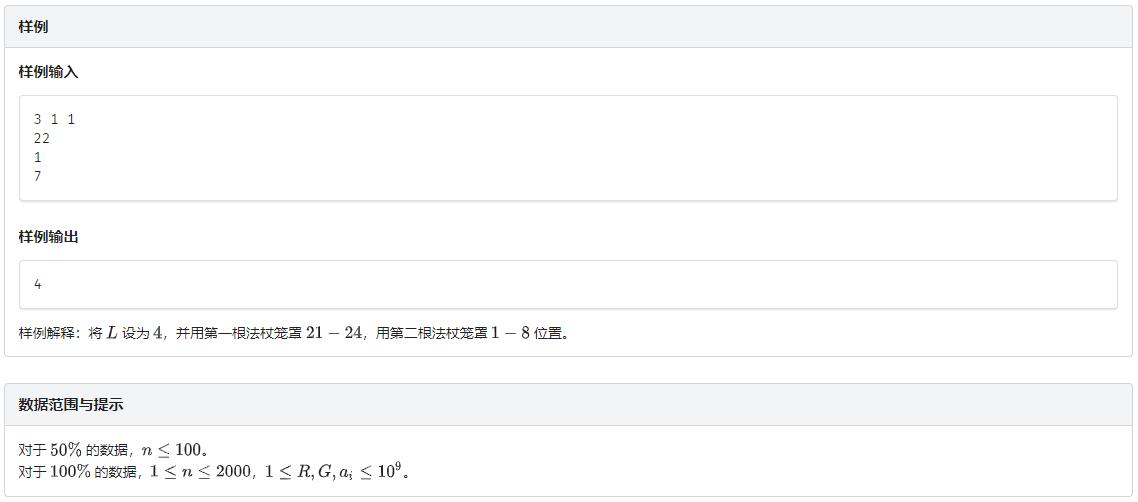
解题思路

二分权杖覆盖长度len

$q[i]$ 表示在第 i 个位置用普通法杖最远可以覆盖到哪个点
$p[i]$ 就是用高级法杖
$q[n+1]=p[n+1]=n$，这样好维护

考虑DP，$f[i][j]$ 表示用 i 个普通法杖和 j 个高级法杖能到的最远点
第 i 个普通法杖，因为 $f[i-1][j]$ 已经用 $i-1+j$ 个法杖覆盖了，所以第 i 个法杖应该在第 $f[i-1][j]+1$ 个法坛用，那么新覆盖到的最远点是$q[f[i-1][j]+1]$
高级法杖同理

因为中间是线性覆盖过去的，最后判断 $f[R][G]$ 到没到n就行了

---

Code

#include <bits/stdc++.h>

using namespace std;

int n, R, G, a[2100], ans, q[2100], p[2100], f[2100][2100];

int check(int len) 
	memset(q, 0, sizeof(q));
	memset(p, 0, sizeof(p));
	memset(f, 0, sizeof(f));
	
	int q1 = 1, p2 = 1;
	for(int i = 1; i <= n; i ++) 
		int q1 = a[i] + len - 1, p2 = a[i] + 2 * len - 1;  //法杖覆盖的距离
		
		int j = i;
		while(q1 >= a[j] && j <= n) j ++;  //最远能覆盖的点
		q[i] = j - 1;
		
		j = i;
		while(p2 >= a[j] && j <= n) j ++;
		p[i] = j - 1;
	
	
	q[n + 1] = p[n + 1] = n;
	for(int i = 0; i <= R; i ++)
		for(int j = 0; j <= G; j ++) 
			if(i > 0) f[i][j] = q[f[i - 1][j] + 1];
			if(j > 0) f[i][j] = max(f[i][j], p[f[i][j - 1] + 1]);
		
	
	return (f[R][G] == n);


int main() 
	scanf("%d %d %d", &n, &R, &G);
	for(int i = 1; i <= n; i ++) scanf("%d", &a[i]);
	sort(a + 1, a + 1 + n);
	if(R + G >= n)  printf("1"); return 0; 
	int l = 1, r = 1e9;
	while(l <= r) 
		int mid = (l + r) >> 1;
		if(check(mid))
			ans = mid, r = mid - 1;
		else l = mid + 1;
	
	printf("%d", ans);