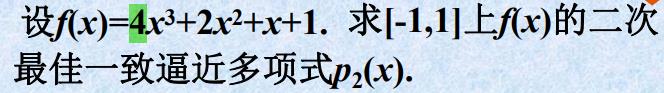《数值分析》-- 正交多项式

Posted 2021-12-29 胜天半月子

文章目录

• 一、正交函数族和正交多项式
• • 1.1 定义
  • 1.2 正交多项式的构造
  • 1.3 正交多项式的性质
• 二、常用的正交多项式⭐
• • 2.1 Legendre(勒让德)多项式
  • 2.2 切比雪夫多项式
  • • 最小零偏差问题

---

一、正交函数族和正交多项式

1.1 定义

1.2 正交多项式的构造

注：${\phi }_n(x)$是最高次项系数为1的$n$次多项式。

1.3 正交多项式的性质

(1) 正交多项式 ${\phi }_0(x)$,${\phi }_1(x)$,…,${\phi }_n(x)$线性无关.
(2) 任一 $n$次多项式$P_n(x)均可表示为 ${\phi }_0(x)$,${\phi }_1(x)$,…,${\phi }_n(x)$的线性组合。



以上性质证明参见课本P58。

---

二、常用的正交多项式⭐

2.1 Legendre(勒让德)多项式

这里的权函数${\rho }_{(}x)$ =1

1. 定义
   
   
2. 性质

• 正交性
  
• 递推关系
  
  
• 奇偶性
  

2.2 切比雪夫多项式

这里的权函数${\rho }_{(}x)=\frac{1}{\sqrt{1-x^2}}$

1. 定义
   
   

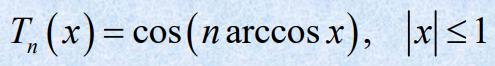
• 性质
  
  
  
  $T_n(x)$是$n$次多项式
  
  
• 奇偶性
  
• 正交性
  

最小零偏差问题

即：$P_n(x)$为0在给定的有界闭区间上最佳一致逼近。
最小0偏差多项式可由$T_n(x)$获得。

• 最佳一致逼近
  
  在[-1,1]上所有首项系数为1的n次多项式$P_n(x)$中,$2^{1-n}{T}_n(x)$对0的偏差最小：
  
  
  
  

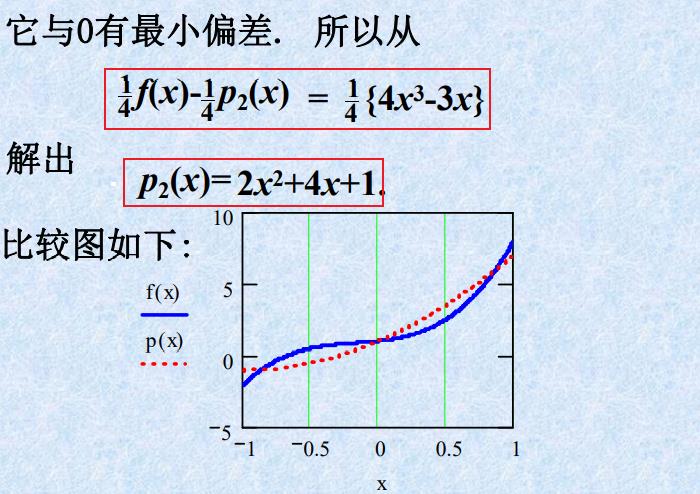
• 例题

1. 
   
   

---