进阶——细赏并查集
Posted 杨枝
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了进阶——细赏并查集相关的知识,希望对你有一定的参考价值。
食物链(Poj 1182 / NOI 2001)
原题描述
题目描述
动物王国中有三类动物 A,B,C,这三类动物的食物链构成了有趣的环形。A 吃 B,B 吃 C,C 吃 A。
现有 N 个动物,以 1 - N 编号。每个动物都是 A,B,C 中的一种,但是我们并不知道它到底是哪一种。
有人用两种说法对这 N 个动物所构成的食物链关系进行描述:
第一种说法是 1 X Y,表示 X 和 Y 是同类。
第二种说法是2 X Y,表示 X 吃 Y 。
此人对 N 个动物,用上述两种说法,一句接一句地说出 K 句话,这 K 句话有的是真的,有的是假的。当一句话满足下列三条之一时,这句话就是假话,否则就是真话。
当前的话与前面的某些真的话冲突,就是假话
当前的话中 X 或 Y 比 N 大,就是假话
当前的话表示 X 吃 X,就是假话
你的任务是根据给定的 N 和 K 句话,输出假话的总数。
输入格式
第一行两个整数,N,K,表示有 N 个动物,K 句话。
第二行开始每行一句话(按照题目要求,见样例)
输出格式
一行,一个整数,表示假话的总数。
输入输出样例
输入
100 7
1 101 1
2 1 2
2 2 3
2 3 3
1 1 3
2 3 1
1 5 5
输出
3
说明/提示
1 ≤ N ≤ 5 ∗ 10^4
1 ≤ K ≤ 10^5
洛谷链接:https://www.luogu.com.cn/problem/P2024
Poj链接:http://poj.org/problem?id=1182
参考代码一(C++版本)
参考代码一逐步落实并查集的各个需要把握的点,并查集模块化学习路途上的一湾清泉 😊😊😊
#include <iostream>
using namespace std;
const int MAX_N = 150030,MAX_K = 100010;
int N,K;//题目要求的输入N只动物和K条信息
int par[MAX_N];//维护父亲结点的信息
int height[MAX_N];//树的高度
//初始化n个元素
void init(int n)
//让自己当自己的父结点
for(int i = 1;i <= n ; i++)
par[i] = i;
height[i] = 1;
//查询树的根
int find(int x)
if(par[x] == x) return x;
else return par[x] = find(par[x]);
//合并x 和 y 所属的集合
void unite(int x,int y)
x = find(x);
y = find(y);
//如果x 和 y在一个集合
if(x == y) return ;
//定义合并的元素原则是将树高小的合并到树高大的
if(height[x] < height[y]) par[x] = y;
else
par[y] = x;
if(height[x] == height[y]) height[x] ++;
// 判断x 和 y 是否属于同一个集合
bool same(int x,int y)
return find(x) == find(y);
int main()
scanf("%d %d",&N,&K);
//初始化并查集
init(N * 3);
int ans = 0;//记录错误答案
//K次操作询问
for(int i = 0; i < K;i++)
int t,x,y;
scanf("%d %d %d",&t,&x,&y);
if(x <0 || x > N || y < 0 || y > N) //现在问题在这里,加入取等号,会出现判断自己出界,假如不取等号,会段错误
ans ++;
continue;
// x , x+N , x+ 2* N 分别表示 x-A,x-B,x-C
if(t == 1)
//这个判断要做的是判断是否为同类,也就是祖先是否相同,三个集合,A和B。A和C是不同的类,但是这里判断出来祖先一样,应该是假话了嘛
if(same(x,y + N) || same(x,y+2*N)) ans ++; //如果在一个集合
else
//不在一个集合就进行合并
unite(x,y);
unite(x+N,y+N);
unite(x+N*2,y+N*2);
else //处理 "x吃y的情况"
if(same(x,y) || same(x,y+2*N)) ans ++;
else
unite(x,y+N);
unite(x+N,y+2 * N);
unite(x + 2*N , y);
printf("%d\\n",ans);
return 0;
深化理解
✨并查集的结构
并查集使用树状结构。每个元素对应这个结点,合并为集合后能够形成对应的树。并查集中最需要的关注的根或者称为老大是谁

✨并查集的主要模块
-
初始化🌈
让自己做自己的老大
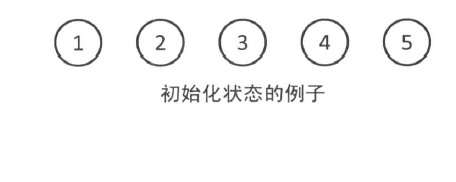
-
合并🌈
像下图一样,从一个组的根向另号一个组的根连边,这样两棵树就变成了一棵树,也就把两个组合并为一个组了。
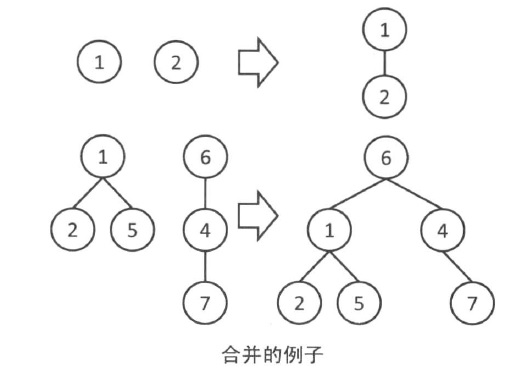
合并的一点好习惯🌈
■对于每棵树,记录这棵树的高度(height)。
■合并时如果两棵树的height不同,那么从height小的向height大的连边。
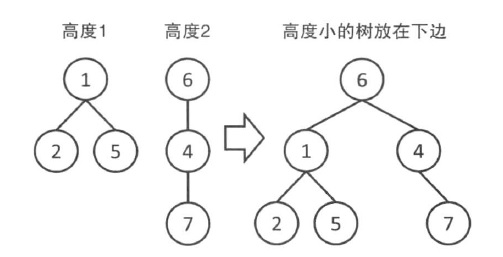
-
查询🌈
为了查询两个节点是否属于同一组,我们需要沿着树向上走,来查询包含这个元素的树的根是谁。
如果两个节点走到了同一个根,那么就可以知道它们属于同一组。
在下图中,元素2和元素5都走到了元素1,因此它们属于同一组。另一方面,由于元素7走到的是元素6,因此同元素2或元素5属于不同组。

✨并查集实现中的注意点
为了防止合并以后,对于查找的复杂度会提高,采用了路径压缩的方式
✨路径压缩
通过路径压缩,可以使得并査集更加高效。
对于每个节点,一旦向上走到了一次根节点,就把这个点到父亲的边改为直接连向根。
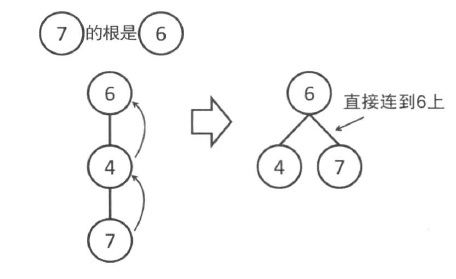
在此之上,不仅仅是所查询的节点,在查询过程中向上经过的所有的节点,都改为直接连到根上。这样再次查询这些节点时,就可以很快知道根是谁了。
✨并查集的实现
前提部分
- 用数组par表示父亲的编号。par数组里面只存放根结点的信息。par[x] == x 时,x就是所在的树的根
int par[MAX_N]; int height[MAX_K]; - 初始化n个元素
for(int i= 1;i <= n ;i++) par[i] = i; height[i] = 1; - 查询树的根
int find(int x) if(par[x] == x) return x; else return par[x] = find(par[x]); - 合并传入参数所属的集合
void unite(int x,int y) x = find(x); y = find(y); if(x == y) return ; if(height[x] < height[y]) par[x] = y; else par[y] = x; if(height[x] == height[y]) height[x] ++; - 判断传入参数是否在同一个集合
bool same(int x,int y) return find(x) == find(y);
✨总结:什么是并查集
通过例题的要求和上文的引述,我们可以总结出来,并查集在维护一些散乱的数据元素的时候,可以高效的管理这些数据。并查集也是一种数据结构,是一种用来管理元素分组情况的数据结构。并查集也被称为不相交集数据结构,研究它的人很多,做出主要贡献的是RobertE.Tarjan,这位大师也是深度优先搜索的发明人之一。
并查集主要作用的范围是
- 查询元素a 和 元素 b是否属于同一个组
- 合并元素a和元素b所在的区间
剖析例题食物链
初步分析 🎯
例题中给了我们很多零散的条件,最后要让我得到一个结果。对于这种须高效地维护关系,并快速判断是否产生了矛盾,并查集就可以很好的发挥作用。对于本题,需要维护的信息有两个:
- ⭐是否是同类
- ⭐是否存在捕食关系
解决思路 🎯
对于每只动物i创建3个元素i-A、i-B、i-C,并用这总共的3*N个元素建立并查集。这个并查集维护如下信息:
■ i-X 表示 i是属于X这个物种(或者说是集合)
■ 并查集里的每一个组表示组内所有元素代表的情况都同时发生或不发生。
例如,如果i-A和j-B在同一个组里,就表示如果i属于物种A那么,j一定属于物种B。因此,对于每一条信息,只需要按照下面进行操作就可以了:
🔗 第一种,x 和 y 属于一个集合,那么合并 x-A 和 y-A, x-B 和 y-B,x-C 和 y-C。
🔗 第二种,x 吃 y,那么合并 x-A 和 y-A, x-B 和 y-B,x-C 和 y-C。
■ 需要注意的是,合并之前要先判断合并操作是否会触发矛盾,比如对于第一种而言,就要先保证x-A 和 y-B 或者 y-C在同一组里。
存在的疑问 🎯
可能有小伙伴想问,为什么无论在不在一个集合里,都要执行合并的操作了?这是为了符合路径压缩的思想,在更多的结点最后都是和根结点直接产生关系,可以实现在数据量庞大的时候,依旧可以快速的执行合并操作。
举个栗子 🎯
在军营里,一个说我比旅长小两级,另一个说,我比军长大一级,另一个又说,我不太行,我只比排长大一点。想想通过这种散乱的描述,要获得有用信息会很困难。
假如换个维护信息的方式,一个说,我比将军小四级,另一个说,我比将军小两级,另一又说,我比将军小七级,最后一个,我就是将军…
那么,很明显的可以体会出来,后一种直接把老大作为维护的根本,那么获得的信息会更有秩序,也会更快。
对于并查集而言,并查集的找到树的根和路径压缩主要就是落实上述的事情,通过不断的和老大建立直接联系,使得查询和修改变得更加容易和轻松。
代码逐步落实 🌺
初始化并查集 🌺
因为本思路通过维护的是三个不同才层次的集合来实现对题中三个物种的区分
元素x代表的是x-A
元素x + N 代表的是x -B
元素x + 2* N 代表的是 x-C
这里对于N可以理解为权重。
处于不带权重的数组中的x就是最基础的物种A
处于带了一层权重N的数组范围的则是物种B
处于带了两层权重的数组范围的则是物种C
/***********全局变量的声明**********/
const int MAX_N = 150030,MAX_K = 100010;
const int MAX_N = 150030,MAX_K = 100010;
int N,K;
int par[MAX_N];//维护父亲结点的信息
int height[MAX_N];//树的高度
/**********主函数*************/
init(N * 3);
K次循环,录入数据,处理数据 🌺
🌀判断假话
- 当前的话与前面的某些真的话冲突,就是假话;
- 当前的话中 X 或 Y 比 N 大,就是假话;
- 当前的话表示 X 吃 X,就是假话。
第一个if解决的是有没有符合范围,不符合范围?假话!❌
现在进入if的都是符合范围的数据
处理情况1:判断是同类
if(same(x,y + N) || same(x,y+2*N)) ans ++;
如果给出的操作是说x 和 y 是同类,但是通过same函数计算出,x所在的物种A和y所在的物种B(y+N 是在物种B所在的数组范围)的祖先相同,或者x所在的物种A和y所在的物种C的祖先一样。这合理吗?这不合理,假话~❌,对于是同一个物种的,就将它们维护起来,方便以后查询
处理情况2:判断捕食的情况
如果给出的操作是说x捕食y,但是我传入的数据中,x和y是同类
same(x,y)
或者x是吃y的,结果算出来祖先一样的
same(x,y+2*N)
这合理吗?这不合理,假话。❌
for(int i = 0; i < K;i++)
int t,x,y;
scanf("%d %d %d",&t,&x,&y);
//当前的话中 X 或 Y 比 N 大,就是假话;
if(x <0 || x > N || y < 0 || y > N)
ans ++;
continue;
if(t == 1)//处理x 和 y 是同类的情况
if(same(x,y + N) || same(x,y+2*N)) ans ++;
else
unite(x,y);
unite(x+N,y+N);
unite(x+N*2,y+N*2);
else //处理 "x吃y的情况"
if(same(x,y) || same(x,y+2*N)) ans ++;
else
unite(x,y+N);
unite(x+N,y+2 * N);
unite(x + 2*N , y);
输出结果,完美解决🚀
printf("%d\\n",ans);
参考代码二(C++版本)
可能有小伙伴想说,我打比赛的时候可没有这个时间一点一点构建函数,好的嘞。它来了~

仙术直通车🚄🚄🚄
#include <iostream>
using namespace std;
const int N = 50010;
int n,m;
//p数组是并查集的父结点,d数组是距离
int p[N],d[N];
//并查集的核心函数
int find(int x)
//如果x不是根节点
if(p[x] != x)
//提前存放上x的父结点通过find函数递归找到的祖宗结点的信息
int t = find(p[x]);
//因为d[x]存放的就是x到它原本的父节点的距离,现在再加等于x的父节点p[x]到根节点的距离,就是x到根节点的距离
d[x] += d[p[x]];
p[x] = t;//更新x父结点的信息,让x的祖宗结点直接当x的父结点
return p[x];
int main()
scanf("%d%d",&n,&m);
//初始化每一个点
for(int i = 1;i <= n;i++) p[i]= i;
int res = 0;//假话的数量
//k次询问
while(m--)
int t,x,y;
scanf("%d%d%d",&t,&x,&y);
if(x > n || y > n) res ++;
else
//找出x 的根节点 px 和 y的根节点py
int px = find(x) , py = find(y);
if(t == 1) //x 和 y是同类的情况
//如果两个是在一颗树上的,但是模出来结果不一样,那就不是同类
if(px == py && (d[x] - d[y]) % 3) res ++;
else if (px != py)
p[px] = py;
d[px] = d[y] - d[x];
else // x 吃 y的情况
//如果在同一颗树上 d[x] 比 d[y]大的时候。x可以吃y
if(px == py && (d[x] - d[y] - 1) % 3) res ++;
else if(px != py)//不在一棵树上,现在把x合并到y这颗树上
p[px] = py;
d[px] = d[y] + 1- d[x];
printf("%d\\n",res);
return 0;
手起刀落,整个代码都清净了 💫

难点解析
参考代码二添加了维护元素到根节点距离的数组d[]。它的作用是为区分不同物种做贡献。
与参考代码一的想法一致,要拿捏住并查集的核心是要和根节点建立直接的联系
模3区分物种
参考代码的逻辑是利用距离来区分不同的物种。A 吃 B,B 吃 C,C 吃 A。形成了一个环。

箭头的方向理解为,某某被送到某某的嘴中,比如物种A指向物种B,就可以理解为A被送到B的嘴中。图中形成的环就代表A 吃 B,B 吃 C,C 吃 A
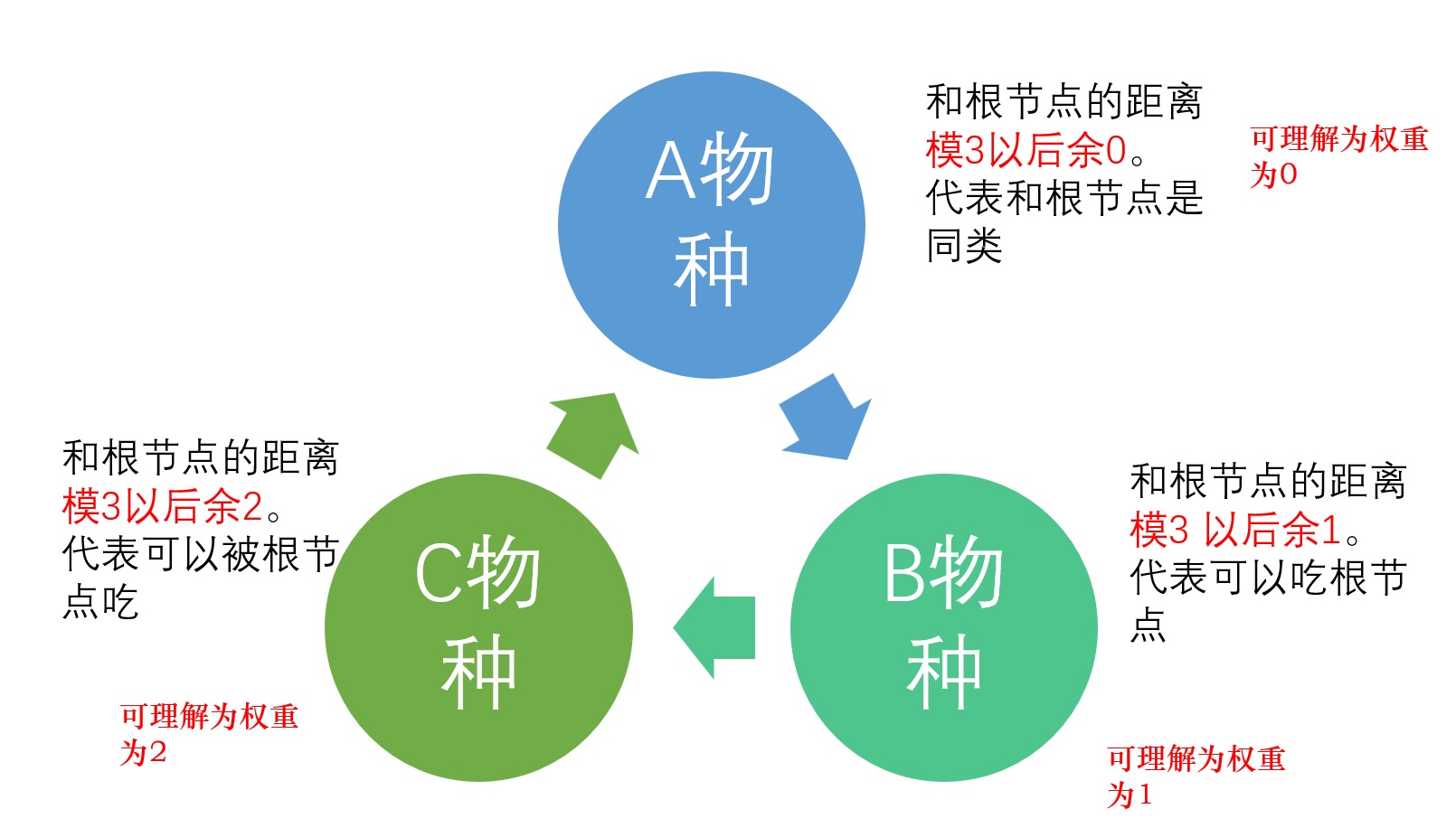
假话判断
-
越界
if(x > n || y > n) res ++; -
对于给定操作是判断同类的情况
- 情况1:x和y在一个集合,算出来根节点一样,但是模出来结果(d[x] - d[y]) % 3 != 0,说明不是同类,这句话是假话❌
if(px == py && (d[x] - d[y]) % 3) res ++;- 情况2:x 和 y 的根节点不同。将x和y维护在一起,并计算维护后,到根节点的距离
可能较难理解的是计算距离😝
在将x合并到y以后,那么它们应该是属于同一个物种了,那么x和y模3以后算出来的值应该相同,对吧😝
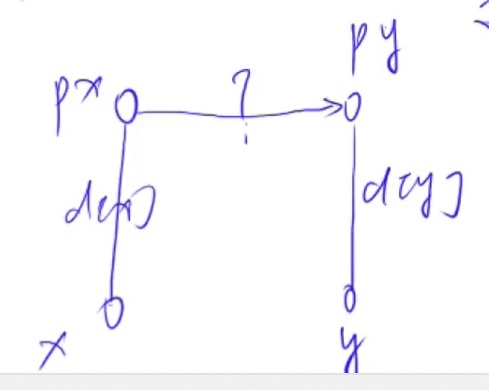
如图,可以得到(d[x] + ? - d[y] ) % 3 = 0,化简得 d[px] = d[y] - d[x];
p[px] = py; d[px] = d[y] - d[x]; -
对于给定操作是x吃y的情况
1.如果x和y在同一颗树上 d[x] 比 d[y]大的时候,结合上文的循环圈图看,也就是x的权重比y的权重大的时候。x可以吃y。
因此,当描述x吃y,且判断出在一个集中,倘若
(d[x] - d[y] - 1) % 3 != 0那么这句话是假话❌
2.剩下的情况是,x和y不在一颗树上,而且是真话,那么将它们维护到一颗树上。
else if(px != py) p[px] = py; d[px] = d[y] + 1- d[x];
写在最后,开心AC😉

谢谢观看,若有偏颇,欢迎指正(^ - ^ )
基础算法持续更新中喔~~~
以上是关于进阶——细赏并查集的主要内容,如果未能解决你的问题,请参考以下文章