17道题带你理解二分查找
Posted 被折叠的小饼干
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了17道题带你理解二分查找相关的知识,希望对你有一定的参考价值。
不太会的可以先看看二分查找的模板
点这里
最需要注意的是二分查找的分界线并不止局限于大于等于小于,而是对某种性质的一种分界
1.Leetcode704. 二分查找
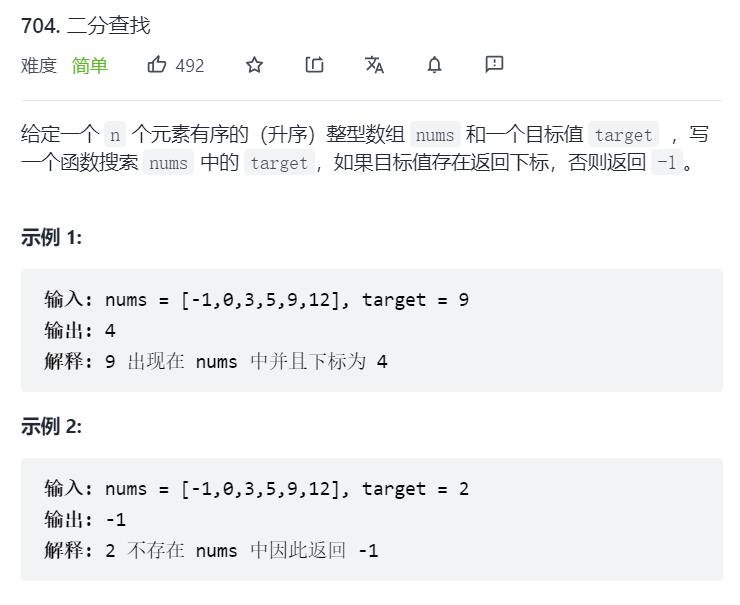
class Solution
public:
int search(vector<int>& nums, int target)
int len=nums.size();
int l=0,r=len-1;
while(l<r)
int mid=(l+r)/2;
if(nums[mid]>=target)
r=mid;
else
l=mid+1;
if(nums[r]!=target)return -1;
return r;
;
2.Leetcode69. Sqrt(x)
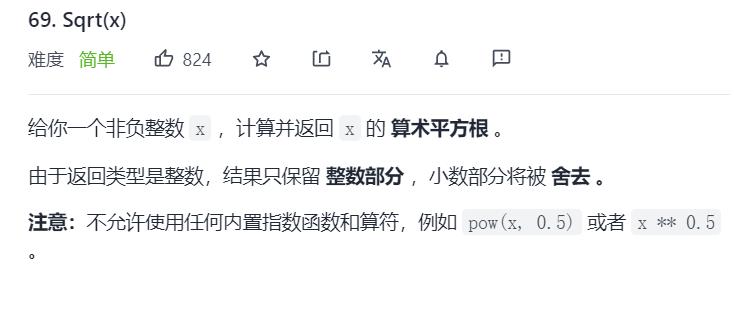
class Solution
public:
int mySqrt(int x)
long long l=0,r=x;
while(r>l)
long long mid=(l+r+1)/2;
if(mid<=x/mid)
l=mid;
else
r=mid-1;
return l;
;
3.Leetcode374. 猜数字大小
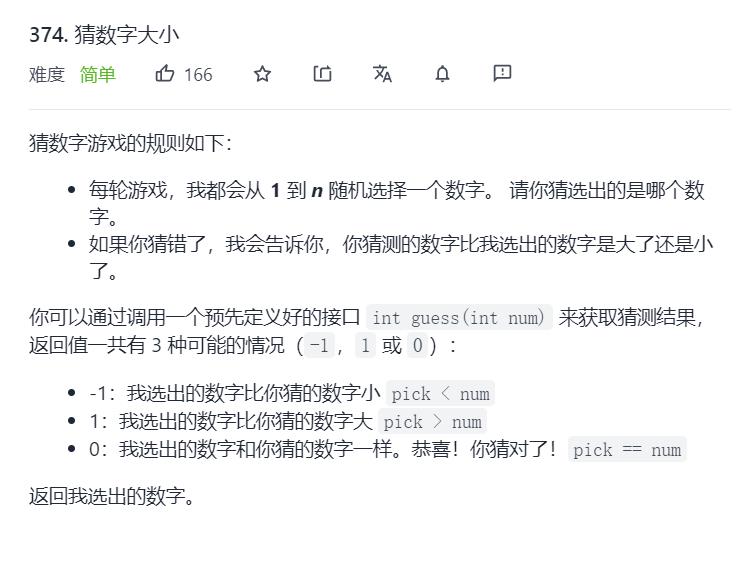
class Solution
public:
int guessNumber(int n)
long long l=1,r=n;
while(l<r)
long long mid=(l+r)/2;
if(guess(mid)==0||guess(mid)==-1)
r=mid;
else
l=mid+1;
return r;
;
4.Leetcode153. 寻找旋转排序数组中的最小值
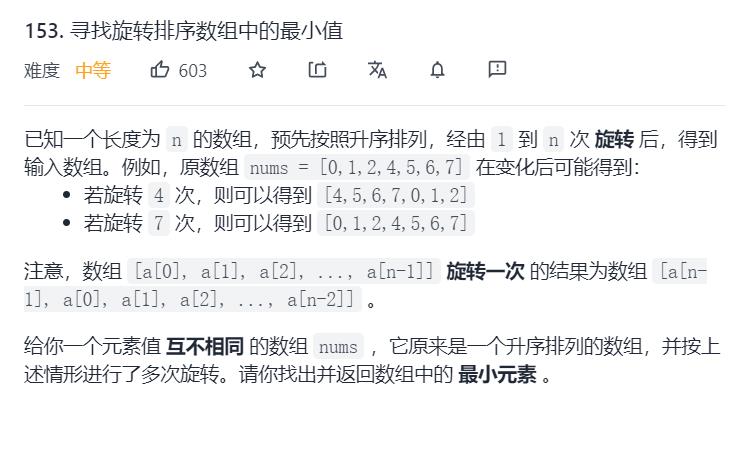
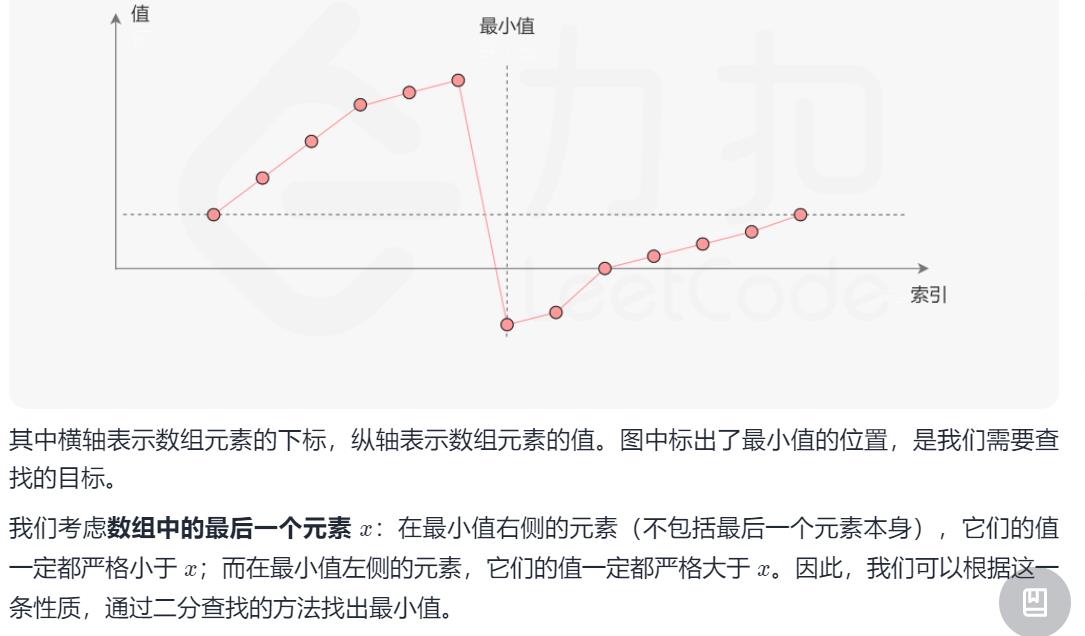
class Solution
public:
int findMin(vector<int>& nums)
int len=nums.size();
int l=0,r=len-1;
int high=nums[len-1];
while(l<r)
int mid=(l+r)/2;
if(nums[mid]<=high)
r=mid;
else
l=mid+1;
return nums[l];
;
5.Leetcode33. 搜索旋转排序数组
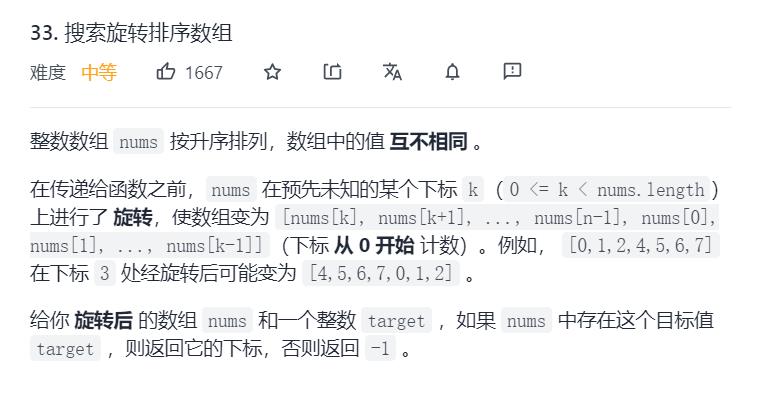
这道题很特别,相较于Leetcode153.寻找旋转排序数组中的最小值
这里找的是目标值target,而不是nums[0],但是target对于153中nums[0]划分的界限(利用最后一个数x作为分界点,小于等于x在nums[0]右边,大于x在nums[0]左边)来说,在这里难以找到循环数组中target是什么性质的分界线,还是需要借助nums[0]和target的位置关系,直接分情况讨论
class Solution
public:
int search(vector<int>& nums, int target)
int len=nums.size(),ans;
int st=find1(nums,0,len-1,nums[len-1]);
printf("st=%d\\n",st);
if(nums[len-1]>=target)
ans=find2(nums,st,len-1,target);
else
ans=find2(nums,0,st-1,target);
if(nums[ans]!=target)return -1;
return ans;
//查找nums[0]的位置,nums[0]的左边都>nums[len-1],右边都小于等于nums[len-1]
int find1(vector<int>&nums,int l,int r,int divide)
while(l<r)
int mid=(l+r)/2;
if(nums[mid]<=divide)
r=mid;
else
l=mid+1;
return l;
//查找target位置,此时查找区间一定是递增的
int find2(vector<int>&nums,int l,int r,int divide)
while(l<r)
int mid=(l+r)/2;
if(nums[mid]>=divide)
r=mid;
else
l=mid+1;
return l;
;
6.Leetcode278. 第一个错误的版本
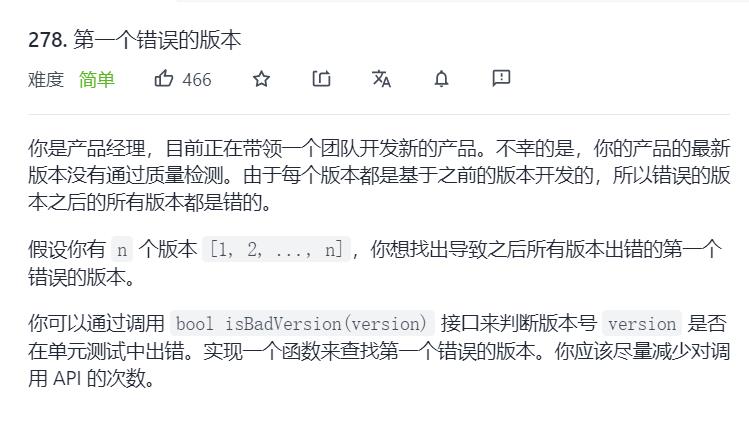
// The API isBadVersion is defined for you.
// bool isBadVersion(int version);
class Solution
public:
int firstBadVersion(int n)
long long l=1,r=n;
while(l<r)
long long mid=(l+r)/2;
if(isBadVersion(mid))
r=mid;
else
l=mid+1;
return l;
;
7.Leetcode162. 寻找峰值
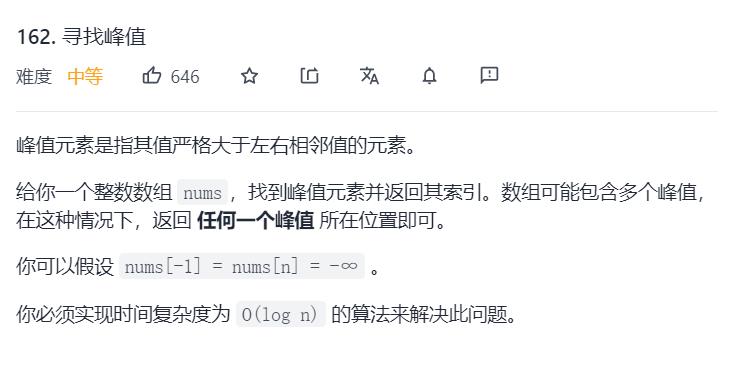
参考Leetcode作者:guanpengchn
首先要注意题目条件,在题目描述中出现了 nums[-1] = nums[n] = -∞,这就代表着只要数组中存在一个元素比相邻元素大,那么沿着它一定可以找到一个峰值
往递增的方向上,二分,一定能找到波峰,往递减的方向只是可能找到,也许没有。
根据上述结论,我们就可以使用二分查找找到峰值
查找时,左指针 l,右指针 r,以其保持左右顺序为循环条件
根据左右指针计算中间位置 m,并比较 m 与 m+1 的值,如果 m 较大,则左侧存在峰值,r = m,如果 m + 1 较大,则右侧存在峰值,l = m + 1
时间复杂度:O(logN)
class Solution
public:
int findPeakElement(vector<int>& nums)
int len=nums.size();
int l=0,r=len-1;
int ans;
while(l<r)
int mid=(l+r)/2;
if(nums[mid]>nums[mid+1])
r=mid;
else
l=mid+1;
return l;
;
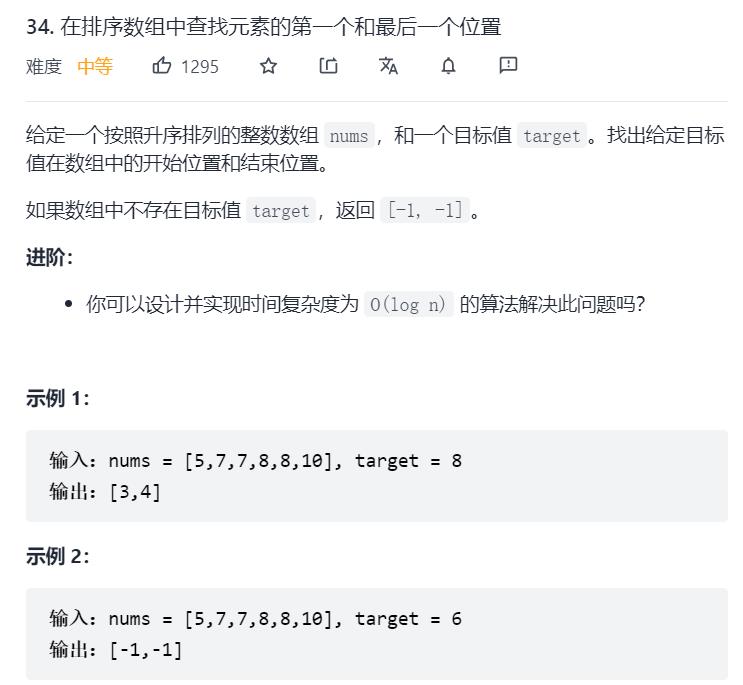
8.Leetcode34. 在排序数组中查找元素的第一个和最后一个位置
class Solution
public:
vector<int> searchRange(vector<int>& nums, int target)
vector<int>ans;
if(nums.size()==0)
ans.push_back(-1);
ans.push_back(-1);
return ans;
int l=findl(nums,target);
int r=findr(nums,target);
if(l==-1||r==-1)
ans.push_back(-1);
ans.push_back(-1);
else
ans.push_back(l);
ans.push_back(r);
return ans;
int findl(vector<int>&nums,int target)
int l=0;int r=nums.size()-1;
while(l<r)
int mid=(l+r)/2;
if(nums[mid]>=target)
r=mid;
else
l=mid+1;
if(nums[l]==target)return l;
return -1;
int findr(vector<int>&nums,int target)
int l=0;int r=nums.size()-1;
while(l<r)
int mid=(l+r+1)/2;
if(nums[mid]<=target)
l=mid;
else
r=mid-1;
if(nums[l]==target)return l;
return -1;
;
9.Leetcode658. 找到 K 个最接近的元素
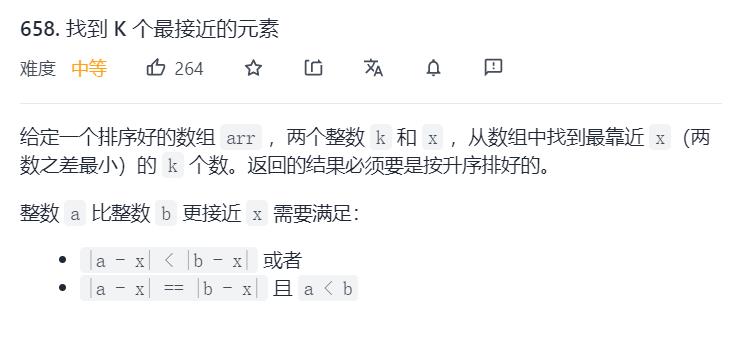
法一:直观地,我们可以将数组中的元素按照与目标 x 的差的绝对值排序,排好序后前 k 个元素就是我们需要的答案。
法二:
①如果target<nums[0],返回前k个数
②如果target>nums[len-1],返回后k个数
③利用二分找到最接近的数,然后不断比较–left,–right与target的绝对值,直到找够k个最小的
class Solution
public:
const int N=1e4+10;
vector<int>ans;
vector<int> findClosestElements(vector<int>& arr, int k, int x)
int len=arr.size();
if(x<=arr[0])
int i=0;
while(k--)
ans.push_back(arr[i++]);
else if(x>=arr[len-1])
int i=len-1;
while(k--)
ans.push_back(arr[i--]);
else
int index=find(arr,x);
//找到最接近的值的下标
if(index-1>=0&&abs(arr[index-1]-x)<=abs(arr[index]-x))index--;//左优先,所以这里是小于等于
if(index+1<len&&abs(arr[index+1]-x)<abs(arr[index]-x))index++;
ans.push_back(arr[index]);
int l=index-1,r=index+1;
while(--k&&l>=0&&r<len)
if(abs(arr[l]-x)<=abs(arr[r]-x))
ans.push_back(arr[l--]);
else
ans.push_back(arr[r++]);
while(k--)
if(l>=0)ans.push_back(arr[l--]);
if(r<len)ans.push_back(arr[r++]);
sort(ans.begin(),ans.end());
return ans;
int find(vector<int>&arr,int x)
int l=0,r=arr.size()-1;
while(l<r)
int mid=(l+r)/2;
if(arr[mid]>=x)
r=mid;
else
l=mid+1;
return l;
;
10.Leetcode50. Pow(x, n)
这道用快速幂好一些
class Solution
public:
const double INF=0x3f3f3f3f;
double myPow(double x, long n)
bool flag=false;
if(n<0)flag=true;
if(flag)n=-n;
double res=qmi(x,n);
if(flag)return 1/res;
return res;
double qmi(double m,long k)
double res=1,t=m;
while(k)
if(k&1)res=res*(double)t;
t=t*t;
k=k>>1;
return res;
;
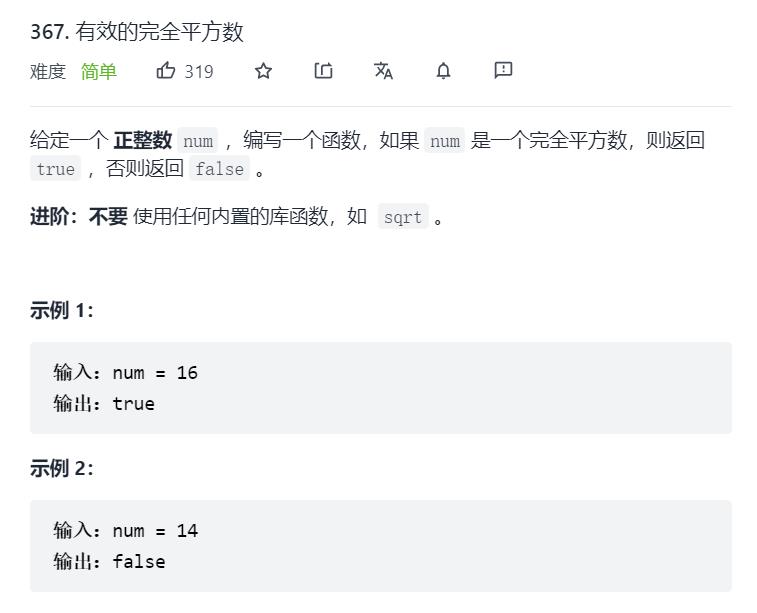
11.Leetcode367. 有效的完全平方数
class Solution
public:
bool isPerfectSquare(int num)
long long l=1,r=num;
while(l<r)
long long mid=(l+r)/2;
if(mid>=num/mid)r=mid;
else l=mid+1;
if(l*l==num)return true;
return false;
;
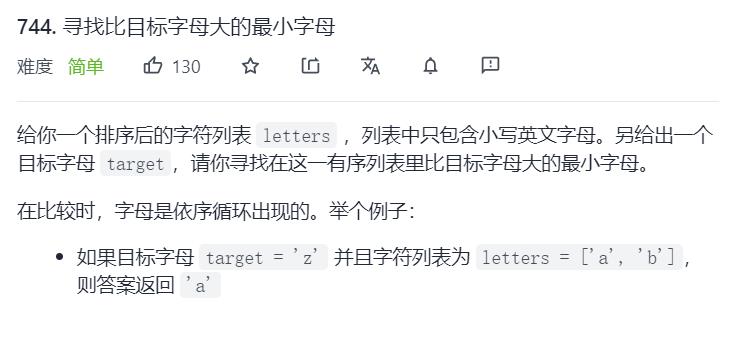
12.Leetcode744. 寻找比目标字母大的最小字母
class Solution
public:
char nextGreatestLetter(vector<char>& letters, char target)
int len=letters.size();
以上是关于17道题带你理解二分查找的主要内容,如果未能解决你的问题,请参考以下文章