算法给小码农计数排序尊者
Posted 小码农UU
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了算法给小码农计数排序尊者相关的知识,希望对你有一定的参考价值。
文章目录

排序
常见的排序算法 扩展
计数排序 不进行数据的比较,而是统计数据出现的次数
思想:计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用。 操作步骤
- 统计相同元素出现次数
- 根据统计的结果将序列回收到原来的序列中
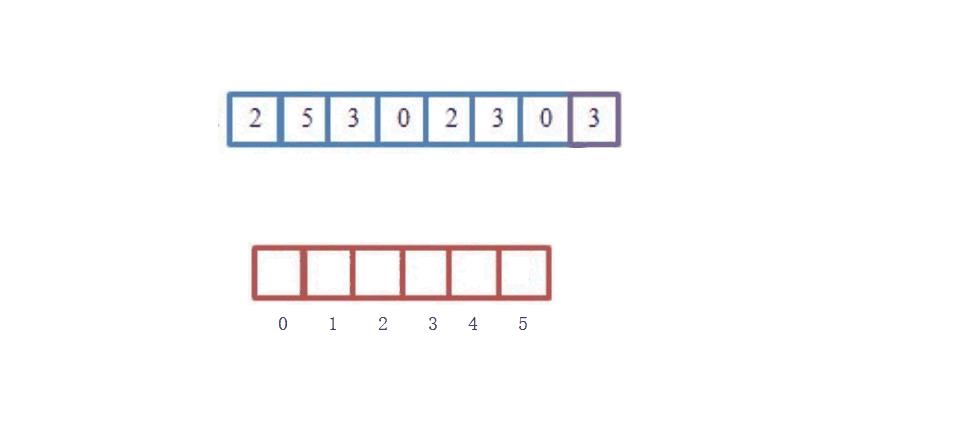

我们可以发现是不是很快,自我感觉一下,没错实际上的确是很快的,时间复杂度是高效到==O(N)==级别的。计数的本质是哈希,所谓的映射
这也会面临一个很现实的问题,就是前面没有时候数,后面1000的位置反而有数,咋处理
eg.1000 1100 1200 1300 1200 1400 1000 1500 1300 1200

我们也可以发现计数排序比较适合大小范围集中的数组

计数排序
// 计数排序
void CountSort(int* a, int n)
assert(a);
int max = a[0], min = a[0];
int i = 0;
for (i = 0; i < n; i++)
if (a[i] > max)
max = a[i];
if (a[i] < min)
min = a[i];
//范围
int range = max - min + 1;
//开辟计数数组
int* count = (int*)malloc(sizeof(int) * range);
//没开辟成功直接错
assert(count);
//数组全部初始化为零
memset(count, 0, sizeof(int) * range);
//统计次数
for (i = 0; i < n; i++)
//相对映射加加
count[a[i] - min]++;
//通过计数数组的次数对原数组进行排序
int j = 0;
for (i = 0; i < range; i++)
while (count[i]--)
//相对映射要回到原数组的数据+min
a[j++] = i+min;
free(count);
count = NULL;
计数排序的特性总结
- 计数排序在数据范围集中时,效率很高,但是适用范围及场景有限。
- 时间复杂度:O(MAX(N,范围))
- 空间复杂度:O(范围)
测性能
1000 一千

10000 一万

100000 十万

1000000 一百万

10000000 一千万

排序总结
稳定性
假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i] = r[j],且r[i] 在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是最稳定的,否则称为不稳定的
再简单一点:数组中相同的值,在排序以后相对位置是否变化
可能会变的,就是不稳定
能保持不变,就是稳定

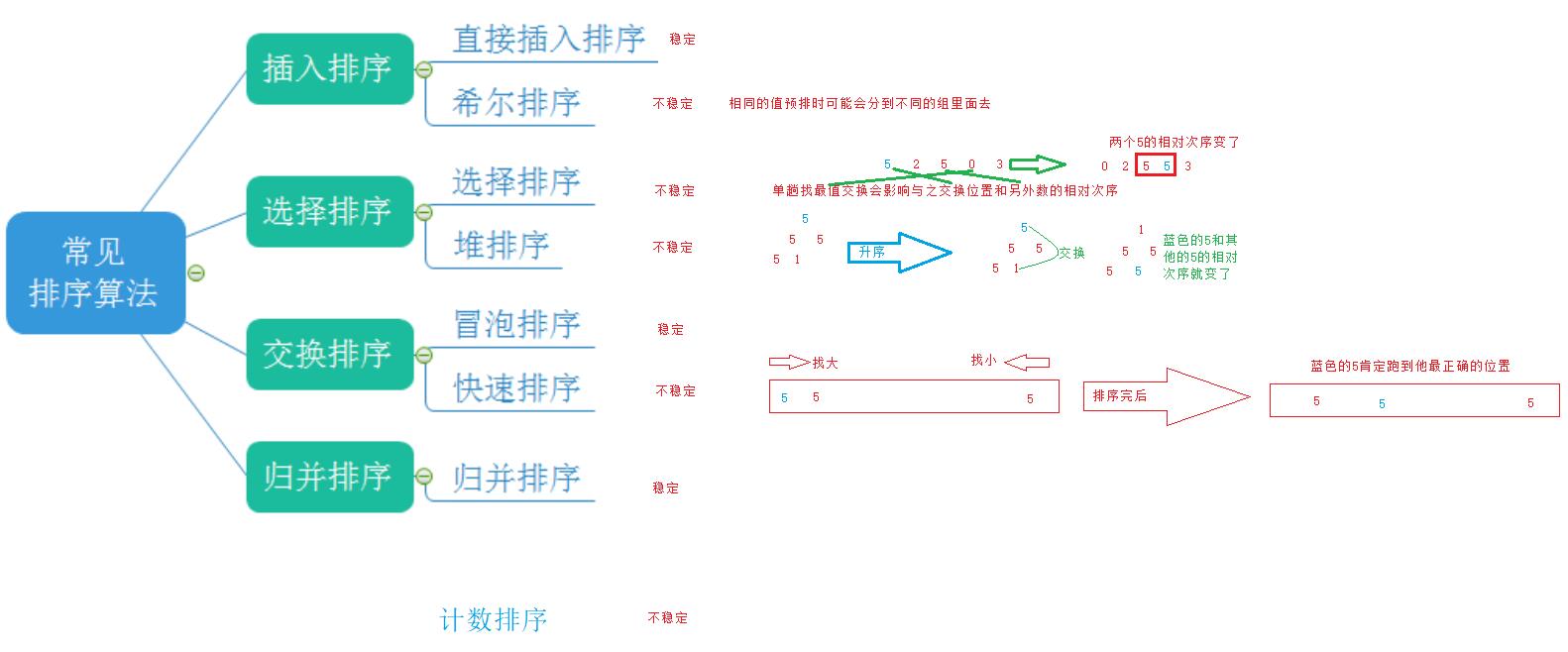
八大排序总结
排序方法 平均时间复杂度 最坏时间复杂度 最好时间复杂度 空间复杂度 稳定性 插入排序 O(N^2) O(N^2) O(N) O(1) 稳定 希尔排序 O(N^1.3) O(N^2) O(N) O(1) 不稳定 选择排序 O(N^2) O(N^2) O(N^2) O(1) 不稳定 堆排序 O(n*logN) O(n*logN) O(n*logN) O(1) 不稳定 冒泡排序 O(N^2) O(N^2) O(N) O(1) 稳定 快速排序 O(n*logN) O(N^2) O(n*logN) 最好O(logN),最坏O(N) 不稳定 归并排序 O(n*logN) O(n*logN) O(n*logN) O(N) 稳定 计数排序 O(MAX(N,range)) O(MAX(N,range)) O(N) O(range) 不稳定
以上是关于算法给小码农计数排序尊者的主要内容,如果未能解决你的问题,请参考以下文章
