SIFT python实现以及公式总结

Posted 2021-12-28 Stratosphere·

SIFT python实现以及公式总结

算法简介

以下来自百度：
  SIFT由David Lowe在1999年提出，在2004年加以完善 [1-2] 。SIFT在数字图像的特征描述方面当之无愧可称之为最红最火的一种，许多人对SIFT进行了改进，诞生了SIFT的一系列变种。SIFT已经申请了专利。
  SIFT特征是基于物体上的一些局部外观的兴趣点而与影像的大小和旋转无关。对于光线、噪声、微视角改变的容忍度也相当高。基于这些特性，它们是高度显著而且相对容易撷取，在母数庞大的特征数据库中，很容易辨识物体而且鲜有误认。使用SIFT特征描述对于部分物体遮蔽的侦测率也相当高，甚至只需要3个以上的SIFT物体特征就足以计算出位置与方位。在现今的电脑硬件速度下和小型的特征数据库条件下，辨识速度可接近即时运算。SIFT特征的信息量大，适合在海量数据库中快速准确匹配。

实验结果对比图

研究sift开始原因是课程作业，在两个星期没日没夜的研究下，翻遍了各大博客，lowe的论文也看了好几遍，终于搞明白了大概过程，特此记录。文中有部分自己实现的源代码，大部分计算过程中的公式我都总结出来了，缺憾是理论部分写的不是很清楚，另一个缺憾是英文水平不够，变量名函数名命名还不够规范。有时间再仔细学理论部分吧，期末周要破大防了orz

实验结果

target和dataset中图片的匹配结果










sift函数调用结果



综合上述对比，target和dataset/3.jpg匹配效果最好，这与实际相符合。对比sift内部函数调用的结果和自己实现的结果，基本吻合，甚至错误匹配比sift更少。对比sift和手写计算出的描述子个数，sift对target生成的描述子个数为1824，匹配个数为427。而自己实现的描述子个数为1829，匹配个数为347，基本持平，侧面说明实现效果较优秀。且对每一张图片生成描述子的时间控制在两分钟以内，不算太慢。

函数实现

SIFT各个函数调用关系

def sift(image):
    print('---------------start sift-----------------')
    image = image.astype('float32')
    image = buildBaseImage(image)
    Octaves = computeOctaves(image.shape)
    GaussPyd = buildGaussPyd(image, Octaves)
    DoGImages = buildDoG(GaussPyd)
    keyPoints = findExtrema(GaussPyd, DoGImages)
    descriptors = buildDescriptors(keyPoints, GaussPyd)
    print('------------------done---------------------')
    return cvt_to_inputImageSize(keyPoints), descriptors

整体关系这张图很形象，取自Alliswell_WP的博客¹

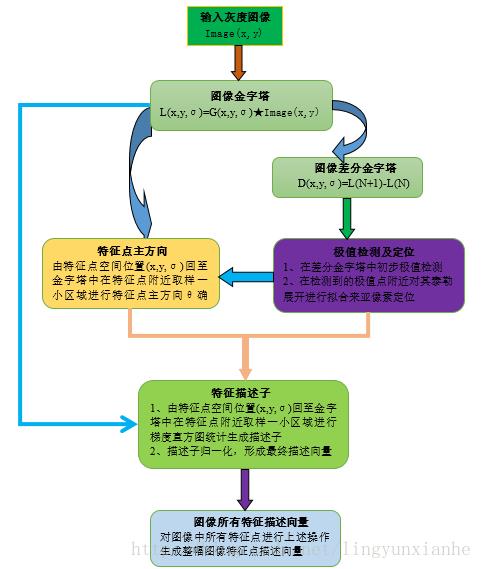
初始化图像

  在建立尺度空间前，Lowe定义原始图像的尺度为0.5，而第0层的尺度为1.6，因此需要先将原始图像扩大一倍，并进行一次高斯模糊使得图像的尺度变成1.6，并能够获取足够多的特征点数量。

  注：想要得到尺度为 ${\sigma }_i$ 的图像，只需要对尺度 ${\sigma }_{i-1}$ 的图像做一次 $\sigma =\sqrt{{\sigma }_i^2-{\sigma }_{i-1}^2}$ 的高斯模糊即可。

代码如下：

def buildBaseImage(img,sigma=1.6):
    img = cv2.resize(img, (0,0), fx=2, fy=2, interpolation = cv2.INTER_LINEAR)
    sigma_diff = sqrt(sigma**2 - 1)
    return cv2.GaussianBlur(img, (0,0), sigmaX=sigma_diff, sigmaY=sigma_diff)

计算高斯金字塔和DoG差分金字塔

  二维图像的尺度空间定义为：
$L(x,y,\sigma )=G(x,y,\sigma )\ast I(x,y)$

  G为标准高斯函数，$\sigma$的大小决定了图像的精细程度，越小越精细，越大越模糊，模拟了不同尺度下的图像。

  我们需要建立一个共有 Octaves 层，每一层含有 S+3 个图像的金字塔。特征为：

1. 每一层的大小是上一层的一半，且每一层中的所有图像大小相同。
2. 其中金字塔的层数定义为：
   
   $Octaves={\log }_2(min(M,N))-a$
   其中a 一般取1~3，M, N 代表图片的大小。
3. 金字塔中 (O, i) 的图像相当于原图做过一个高斯核为 $\sigma =1.6\ast 2^{O+\frac{i}{S}}$ 的高斯模糊后生成的图像。

这个金字塔即为高斯金字塔。详细公式见图，此处引用Alliswell-WP¹ 博客中的图片

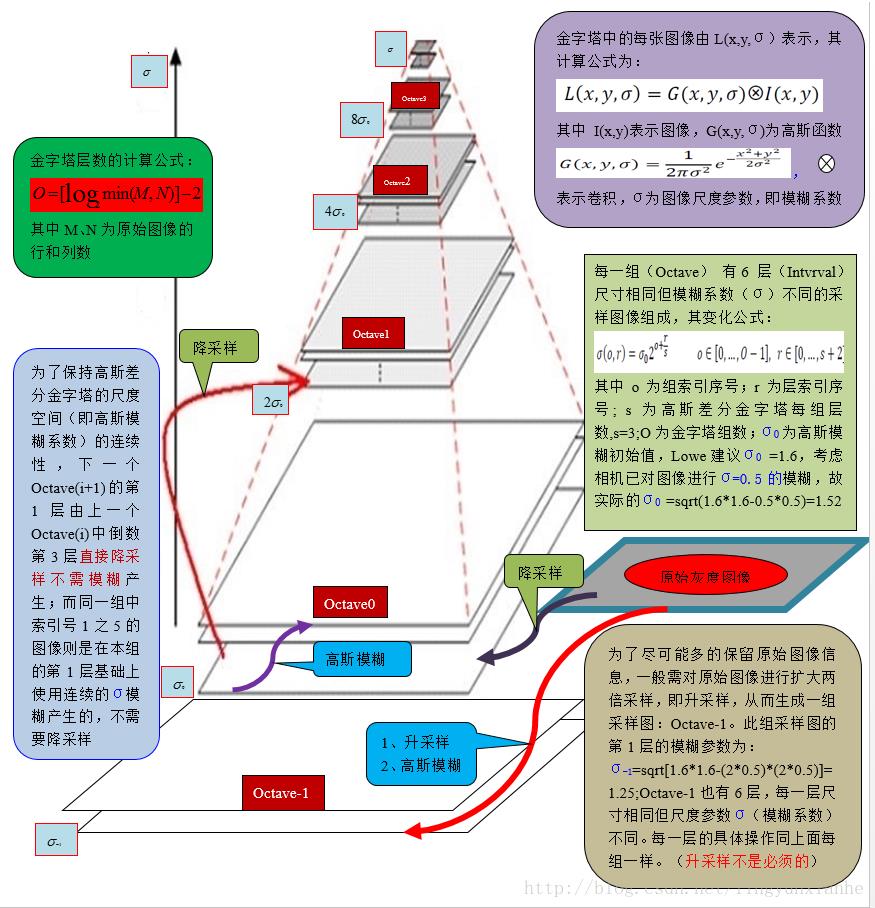
算法思想如下：

  显然，由上述特征以及高斯模糊的叠加性质可以发现，每一层第二张图片开始只需要选择如下数组中的高斯核 [ $k\sigma$ , $k^2\sigma$ , $k^3\sigma$ ,… ] 对第一张图片做高斯模糊即可，而第一张图片为保证高斯空间的连续性，选择上一层中倒数第3张图片直接缩小一倍得到。这样获得的每一张图片根据高斯模糊的叠加性质即符合高斯金字塔的特征。

高斯核数组的生成：

def computeSigma(sigma=1.6, S=3):
    k = 2 ** (1. / S)
    sigma_diff = np.zeros(S+3)
    sigma_diff[0] = sqrt(sigma**2 - 1)
    pre_sigma = sigma 
    for image_index in range(1,S+3):
        cur_sigma = pre_sigma * k
        sigma_diff[image_index] = sqrt(cur_sigma**2 - pre_sigma**2)
        pre_sigma = cur_sigma
    return sigma_diff

按照上述算法思想，算法如下

def buildGaussPyd(image, Octaves, S=3, sigma=1.6):
    GaussPyd = []
    sigma_diff = computeSigma(sigma)
    # 只需要计算第一层的即可，之后每多一层，自然会多乘一次
    for octaves_index in range(Octaves):
        Gauss_images = [image]
        for sigma_kernel in sigma_diff[1:]:
            image = cv2.GaussianBlur(image, (0, 0), sigmaX=sigma_kernel, sigmaY=sigma_kernel)
            Gauss_images.append(image)
        GaussPyd.append(Gauss_images)
        image = Gauss_images[-3]
        image = cv2.resize(image, (int(image.shape[1] / 2),int(image.shape[0] / 2)),interpolation=cv2.INTER_NEAREST)
    return np.array(GaussPyd,dtype=object)

  高斯差分尺度空间定义为：
$D(x,y,\sigma )=L(x,y,k\sigma )-L(x,y,\sigma )$
高斯差分尺度空间由定义即相邻图片作差即可得到

def buildDoG(GaussPyd):
    print("generating DoG...")
    DoGImages = []
    for GaussImages_In_Octaves in GaussPyd:
        DoG_In_Octaves = []
        for i in range(len(GaussImages_In_Octaves)-1):
            DoG_In_Octaves.append(cv2.subtract(GaussImages_In_Octaves[i+1],GaussImages_In_Octaves[i]))
        
        DoGImages.append(DoG_In_Octaves)
    return np.array(DoGImages, dtype=object)

寻找关键点

DoG空间极值点

  寻找关键点的第一步是在DoG金字塔每一组中第二层至倒数第二层中寻找空间极值点，舍弃第一层和倒数第一层。判断是否为空间极值点标准为：将该点和周围8个相邻像素点以及上下两个相邻尺度中2*9个像素点共26个像素点比较，判断是否为极值点。为提高计算的稳定性，舍弃了图像边缘的检索，边缘间隔设定为5.

def isPixelAnExtremum(first_subimage, second_subimage, third_subimage, threshold):
    center_val = second_subimage[1,1]
    if abs(center_val) > threshold:
        # 忽略极值过小的点
        if center_val > 0:
            # 极大值点
            return np.all(center_val >= first_subimage) and \\
                    np.all(center_val >= second_subimage) and \\
                   np.all(center_val >= third_subimage)
        elif center_val < 0:
            # 极小值点
           return np.all(center_val <= first_subimage) and \\
                    np.all(center_val <= second_subimage) and \\
                    np.all(center_val <= third_subimage)
    else:
        return False

关键点精确定位与过滤

对于关键点，设image_index为某一层中该图片的编号，我们定义在三维平面上关键点函数 $f(x,y,image\_index)=D(x,y,image\_index)$

  对于DoG空间极值点，需要精确确定关键点的位置和尺度，这里采用牛顿法确定极值点（你说巧不巧，研究的时候正好凸优化学了牛顿法求极值点）。函数取泰勒展开式展开至二阶，如图：




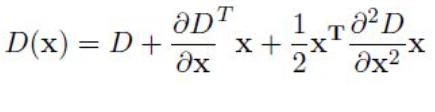
对上述式子求导，令导数等于0，即可得到极值点的偏移量为：




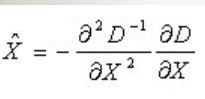
当偏移量在任一维度上的偏移量大于0.5时（即x或y或 image_index），意味着插值中心已经偏移到它的邻近点上，所以必须改变当前关键点的位置。同时在新的位置上反复插值直到收敛；也有可能超出所设定的迭代次数或者超出图像边界的范围，此时这样的点应该删除。
对于图像像素点中的求导方式，通过如下方式计算：



注： 在后续有关坐标(x, y)的计算中，本文采取了和网上大多数源码一致的方式，即对于numpy内置的矩阵行和列，行作为y，列作为x。

y 
|  1  1   1
|  1  1   P
|  1  1   1
O —— —— —— ——x

如图矩阵，则 P(1, 2) = Mat(2, 1)， 显然x，y和矩阵的行和列下标正好相反！这一点在代码实现中体现较为重要。


牛顿法实现如下

SIFT_MAX_INTERP_STEPS = 5
is_suitable_Extrema = False
atempt = 0
while atempt < SIFT_MAX_INTERP_STEPS:
    first_image, second_image, third_image = DoGImages_In_Octave[image_index-1:image_index+2]
    pixel_cube = np.stack([first_image[i-1:i+2, j-1:j+2],
                        second_image[i-1:i+2, j-1:j+2],
                        third_image[i-1:i+2, j-1:j+2]]).astype('float32') / 255.
    image_shape = first_image.shape
    gradient = computeGradient(pixel_cube)
    Hessian = computeHessian(pixel_cube)
    X_bar = -np.linalg.lstsq(Hessian, gradient, rcond=None)[0]
    if np.all( abs(X_bar) < 0.5 ):
        # 极值点收敛
        is_suitable_Extrema = True
        break
    i += int(round(X_bar[1]))
    j += int(round(X_bar[0]))
    image_index += int(round(X_bar[2]))
    if i < image_border_width or i >= image_shape[0] - image_border_width \\
        or j < image_border_width or j >= image_shape[1] - image_border_width \\
            or image_index < 1 or image_index > S:
            break
    atempt += 1

对于最终精确定位的极值点，我们还需要去除极值点小于某一个经验值的极值点，即若 $abs(f)<\frac{T}{S}$ ，则去除该极值点。

边缘响应点检测

  除了DoG响应较低的点，还有一些响应较强的点也不是稳定的特征点。DoG对图像中的边缘有较强的响应值，所以落在图像边缘的点也不是稳定的特征点。Lowe通过计算图像的二阶求导矩阵，即Hessain矩阵，得到其较大的特征值 ${\lambda }_{max}$ 和较小的特征值 ${\lambda }_{min}$， 令$\frac{{\lambda }_{max}}{{\lambda }_{min}}=ratio$，若ratio值越大，说明图像在某一个方向梯度值越大， 另一个方向则越小，这恰好是边缘图像的特征；反之，若比例接近于1，则说明，该点附近较为平缓。若想过滤掉边缘点，则可以通过定义一个阈值 r ，当比值大于 r 时过滤掉。为减少计算，Lowe通过如下推导，得到一个判断条件：





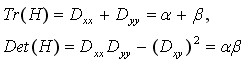
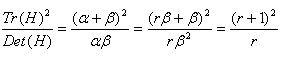
若
$\frac{Tr(H{)}^2}{Det(H)}>\frac{(r+1{)}^2}{r}$ ，则判定为边缘点，舍去。Lowe建议取 $r=10$

源代码实现

  综合上述分析，极值点的筛选需要通过四个步骤的筛选和调整，分别为：

1. 判断该像素点是否为周围3x3x3像素空间的极值点
2. 通过牛顿法精确确定该像素点的极值
3. 该极值点归一化后不能小于某一个经验值，默认threhold取0.03，但在opencv中使用了 $\frac{0.04}{S}$
4. 边缘点检测，满足条件 $\frac{Tr(H{)}^2}{Det(H)}<=\frac{(r+1{)}^2}{r}$

当一个极值点通过了上述四个步骤的筛选和调整，则可以认定为一个极值点，在我的实现中，采取了字典来存储该极值点的位置信息(x, y, octave, image_index)，以及该组中的尺度差值 ${\sigma }_{oct}=1.6\ast 2^{\frac{image\_index}{S}}$

以上是关于SIFT python实现以及公式总结的主要内容，如果未能解决你的问题，请参考以下文章

卡尔曼滤波的原理以及Matlab和python代码实现

python-应用OpenCV和Python进行SIFT算法的实现

机器学习之神经网络的公式推导与python代码（手写+pytorch）实现

Python实现sift算法

python常用代码片段总结

什么库能够在 Python 中提取 SIFT 特征？