信号与系统 2023（春季） 作业参考答案 - 第二次作业

Posted 2023-03-12 卓晴

• 信号与系统 2023（春季） 作业要求 - 第二次作业
• 信号与系统分析2022春季作业-参考答案：第二次作业

 

01 基础练习

---

一、信号的直流分量

1、必做题

  （1）全波整流信号

◎ 解答：

  下面是该信号的波形，信号是周期信号。

▲ 图1.1.1 信号波形

  信号的直流分量为：

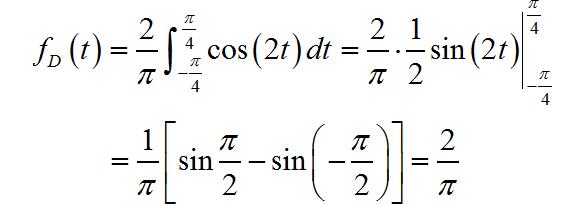
  信号的交流分量为：

  （2） 周期矩形信号

◎ 解答：

  下面是该信号的波形：

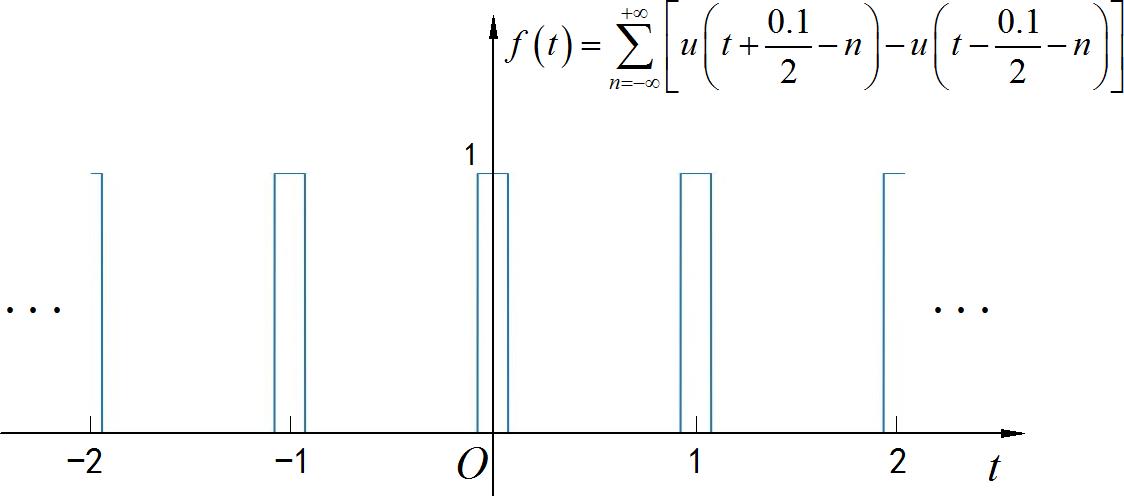
▲ 图1.1.2 信号波形

  信号的直流分量：

  信号的交流分量：

  （3） 周期冲激信号

◎ 解答：

▲ 图1.1.3 信号波形

  信号的直流分量：

  信号的交流分量：

from headm import *

def fun(t):
    f = t*0
    for id,tt in enumerate(t):
        if abs(tt-int(tt)) < 0.001: f[id] = 1

    return f

t = linspace(-2.5, 2.5, 10000)
ft = fun(t)

plt.axis([min(t),max(t), -0.2, 2])
plt.plot(t, ft)

for n in range(-2, 3):
    plt.arrow(n, 1, 0.0, 0.0, shape='full', lw=0, head_width=0.05)

plt.xlabel("t")
plt.ylabel("f(t)")
plt.tight_layout()
plt.show()

  （4）非周期信号

◎ 解答：

  信号的波形如下图所示：

▲ 图1.1.4 信号波形

  信号的直流分量为： 0.5；

  信号的交流分量为：

二、信号奇偶分解

1、必做题

  （1） 奇偶分解

  分别绘制出下面有限长信号与序列的奇分量与偶分量。

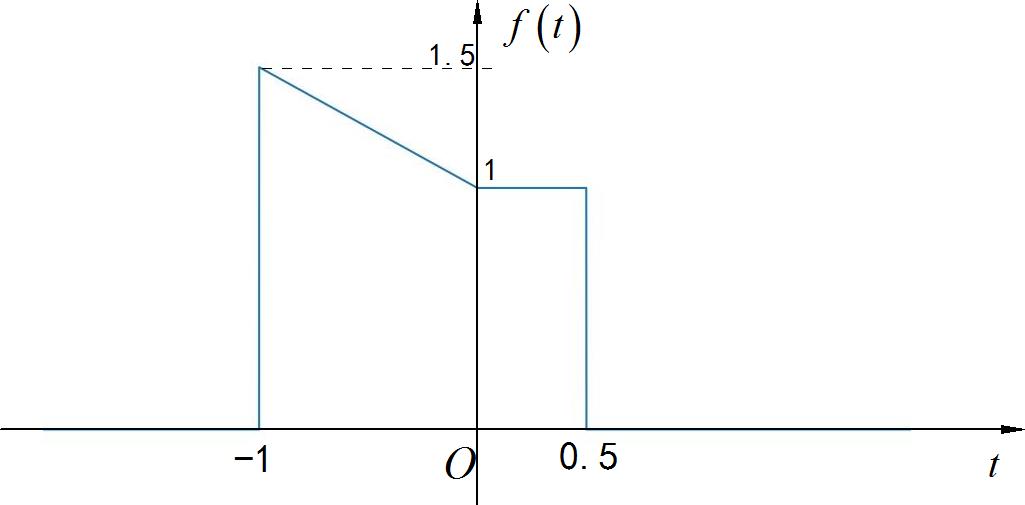
▲ 图1.2.1 连续时间信号

◎ 解答：

▲ 图1.2.2 信号的偶分量

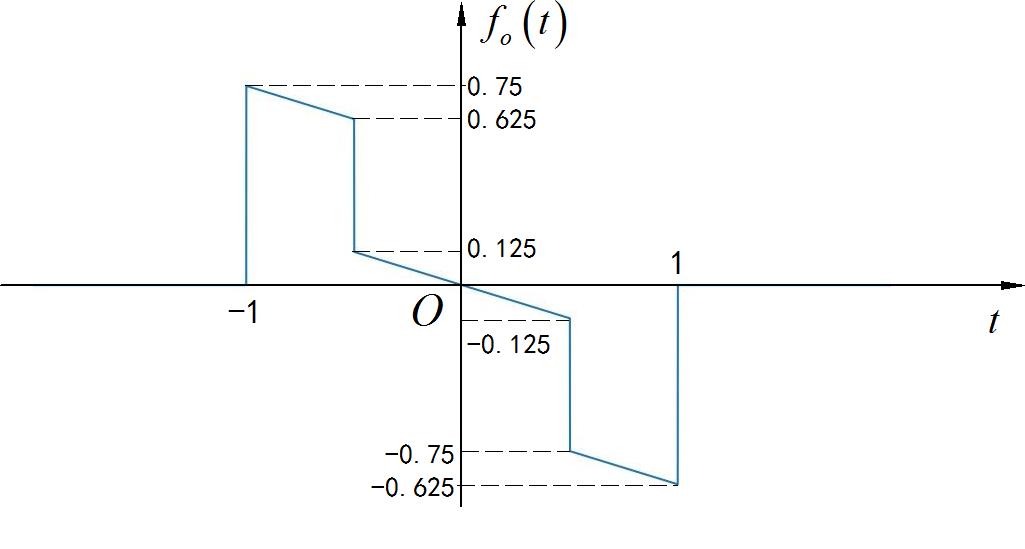
▲ 图1.2.3 信号的奇分量

from headm import *

def G(t0, t1):
    return heaviside(t-t0,0.5)-heaviside(t-t1,0.5)
def fun(t):
    f = (-0.5*t+1)*G(-1,0) + G(0,0.5)
    return f
t = linspace(-2, 2, 10000)
ft = fun(t)
ft1 = ft[::-1]

fte = (ft+ft1)/2
fto = (ft-ft1)/2

plt.axis([min(t),max(t), -0.2, 2])
plt.plot(t, ft)

plt.xlabel("t")
plt.ylabel("f(t)")
plt.tight_layout()
plt.show()

▲ 图1.2.4 离散时间序列信号

from headm import *

startn = -6
endn = 6
t = linspace(startn, endn, endn-startn+1, endpoint=True)
ft = array([0,0,0,1,1,1,1,-0.5,-0.5,-0.5,0,0,0])

markerline, stemline, baseline = plt.stem(t, ft)
plt.setp(markerline, markersize=10)

plt.xlabel("t")
plt.ylabel("f(t)")
plt.axis([min(t)+0.5, max(t)-0.5, -1.5, 1.5])
plt.tight_layout()
plt.show()

◎ 解答：

▲ 图1.2.5 离散时间序列信号的偶分量

▲ 图1.2.6 离散时间序列信号的奇分量

from headm import *

startn = -6
endn = 6
t = linspace(startn, endn, endn-startn+1, endpoint=True)
ft = array([0,0,0,1,1,1,1,-0.5,-0.5,-0.5,0,0,0])
ft1 = ft[::-1]
fte = (ft+ft1)/2
fto = (ft-ft1)/2

markerline, stemline, baseline = plt.stem(t, fto)
plt.setp(markerline, markersize=10)

plt.xlabel("t")
plt.ylabel("f(t)")
plt.axis([min(t)+0.5, max(t)-0.5, -1.5, 1.5])
plt.tight_layout()
plt.show()

  （2） 求解原信号波形

  根据已知的信号 $x\left(t\right)$ 偶分量与右半边波形， 绘制出原始信号 $x\left(t\right)$ 的波形。

▲ 图1.2.7 信号的偶分量

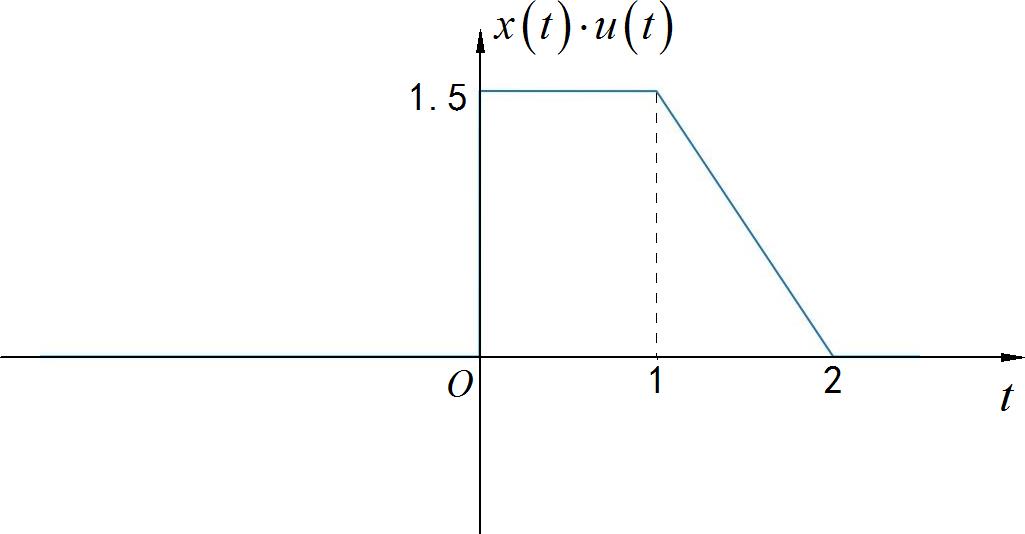
▲ 图1.2.8 信号的因果部分

◎ 求解：

  根据 $$\left[x\left(t\right)-x_e\left(t\right)\right]\cdot u\left(t\right)=x_o\left(t\right)\cdot u\left(t\right)$$ 可以获得信号奇分量的因果部分。

▲ 图1.2.9 奇分量的因果部分

  根据奇分量的对称性， 可以绘制出信号完整的奇分量。

▲ 图1.2.10 信号的奇分量

  将信号的奇分量于偶分量叠加，可以得到信号的完整的波形。

▲ 图1.2.11 信号的完整波形

from headm import *

def G(t, startn, endn):
    return heaviside(t-startn,0.5) - heaviside(t-endn,0.5)

def fune(t):
    return t * G(t, 0, 1) - t * G(t, -1, 0)

def fune1(t):
    return t * G(t, 0, 1)

def fun1(t):
    return 1.5*G(t, 0, 1) - 1.5*(t-2)*G(t, 1, 2)

t = linspace(-2.5, 2.5, 100000)
ft = fune1(t)
ft1 = fun1(t)

fto1 = ft1-ft
fto2 = -fto1[::-1]

fto = fto1+fto2
fte = fune(t)

plt.plot(t, fte+fto)

plt.xlabel("t")
plt.ylabel("f(t)")
plt.axis([min(t), max(t), -1.6, 1.6])
plt.tight_layout()
plt.show()

2、选做题

  （1） 信号进行奇偶分解

  绘制出下面连续时间信号与离散时间序列的奇分量与偶分量。

▲ 图1.2.13 连续时间信号

◎ 求解：

▲ 图1.2.13 信号的偶分量

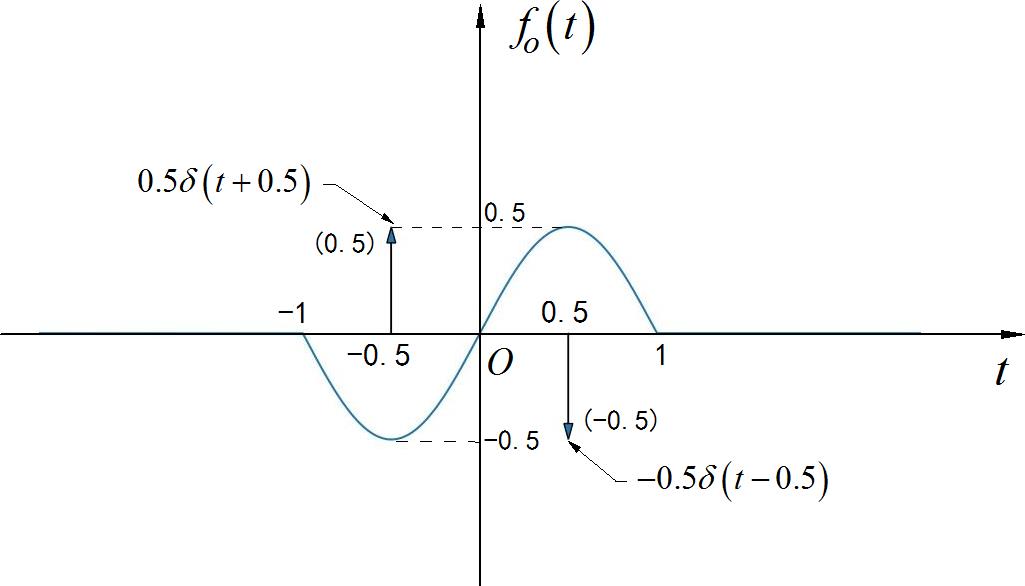
▲ 图1.2.14 信号的奇分量

from headm import *

def G(t, startn, endn):
    return heaviside(t-startn,0.5)-heaviside(t-endn,0.5)

def Gt(t, center, width):
    startn = center-width/2
    endn = startn + width
    return heaviside(t-startn,0.5)-heaviside(t-endn,0.5)

def fun(t):
    return sin(t*pi)*G(t,0,1) #+ Gt(t, -0.5, 0.001)

t = linspace(-2.5, 2.5, 100000)
ft = fun(t)
ft1 = ft[::-1]
fte = (ft+ft1)/2
fto = (ft-ft1)/2

plt.plot(t, fto)
plt.arrow(-0.5, 0, 0.0, 0.5, shape="full", lw=1, length_includes_head=True, head_width=0.05)
plt.arrow(0.5, 0, 0.0, -0.5, shape="full", lw=1, length_includes_head=True, head_width=0.05)

plt.xlabel("t")
plt.ylabel("ft")
plt.axis([min(t), max(t), -1.0, 1.5])
plt.tight_layout()
plt.show()

▲ 图1.2.15 反因果单位阶跃序列

◎ 求解：

▲ 图1.2.16 信号的偶分量序列

▲ 图1.2.17 信号的奇分量序列

from headm import *

startn = -5
endn = 5

n = linspace(startn, endn, endn-startn+1, endpoint=True)
fn = array([0]*len(n))
fn[where(n<=0)]=1

fn1 = fn[::-1]
fne = (fn+fn1)/2
fno = (fn-fn1)/2

markerline,_,_ = plt.stem(n, fno)
plt.setp(markerline, markersize=10)

plt.xlabel("n")
plt.ylabel("f[n]")
plt.axis([min(n)-0.5, max(n)+0.5, -1, 1.5])
plt.tight_layout()
plt.show()

三、信号尺度变换

  已知离散时间序列信号 $f\left[n\right]$ 与连续时间信号 $f\left(t\right)$ 的波形如下图所示， 请根据后面给出的表达式绘制出对应自变量变化后的信号波形。

▲ 图1.3.1 离散时间序列

from headm import *

startn = -5
endn = 5

n = linspace(startn, endn, endn-startn+1, endpoint=True)
fn = array([0.0]*len(n))
fn[where(n==-1)]=0.5
fn[where(n>=0)] = 1
fn[where(n==5)] = 0

fn1 = fn[::-1]
fne = (fn+fn1)/2
fno = (fn-fn1)/2

markerline,_,_ = plt.stem(n, fn)
plt.setp(markerline, markersize=10)

plt.xlabel("n")
plt.ylabel("f[n]")
plt.axis([min(n)-0.5, max(n)+0.5, -1, 1.5])
plt.tight_layout()
plt.show()

▲ 图1.3.2 连续时间信号

from headm import *

def G(t, startn, endn):
    return heaviside(t-startn,0.5)-heaviside(t-endn,0.5)

def Gt(t, center, width):
    startn = center-width/2
    endn = startn + width
    return heaviside(t-startn,0.5)-heaviside(t-endn,0.5)

def fun(t):
    return -1/3*t*G(t, -3, 0)
    
t = linspace(-3.5, 3.5, 100000)
ft = fun(t)
ft1 = ft[::-1]
fte = (ft+ft1)/2
fto = (ft-ft1)/2

plt.plot(t, ft)
plt.arrow(1, 0, 0.0, 1, shape="full", lw=1信号与系统 2023（春季） 作业要求 - 第三次作业

 2021年春季学期-信号与系统-第十二次作业参考答案
 2021年春季学期-信号与系统-第十一次作业参考答案
 2021年春季学期-信号与系统-第十三次作业参考答案
 2021年春季学期-信号与系统-第十五次作业参考答案
 2021年春季学期-信号与系统-第十四次作业参考答案