现代信号处理 18 - 随机过程的线性预测

Posted 2021-12-28 Ciaran-byte

随机过程的线性预测

文章目录

• 随机过程的线性预测
• • 1. 随机过程线性预测问题
  • • 1.1 问题引入
    • 1.2 公式解读
    • 1.3 白噪声的预测误差分析
  • 2. 相关矩阵的正定性
  • • 2.1 问题描述与结论
    • • 2.1.1 相关矩阵的建立
      • 2.1.2 相关矩阵的性质
      • 2.1.3 相关矩阵正定性的结论
    • 2.2 证明
  • 3. 完美预测
  • • 3.1 相关矩阵的奇异性
    • 3.2 相关矩阵完全奇异
    • 3.3 相关矩阵部分奇异
    • 3.4 小结
  • 4. 非完美预测
  • • 4.1 非完美预测的条件
    • 4.2 谱分解
    • 4.3 线性代数分析法与预测误差
    • • 4.3.1 相关矩阵的LU分解
      • • 4.3.1.1 Cholesky分解
        • 4.3.1.2 递推关系
      • 4.3.2 误差模的平方与LU分解的关系
      • • 4.3.2.1 误差的表示
        • 4.3.2.2 误差模的期望的表示
    • 4.5 复变函数分析法与谱分解
    • • 4.5.1 谱分解问题的求解
      • • 4.5.1.1 B(Z)的表示式
        • 4.5.1.2 B(Z)的求解
    • 4.6 复变函数分析法与线性代数分析法的统一
    • • 4.6.1 两个结果
      • 4.6.2 Kolmogorov 等式
      • 4.6.3 Kolmogorov-Szago 等式
  • 5. 总结

1. 随机过程线性预测问题

1.1 问题引入

  前面介绍了一些线性预测的方法，比如levension迭代。但是，现在我们想要知道，对随机信号进行线性预测，究竟能够达到一个怎么样的程度。

  我们先把线性预测问题重申一下，假设我们要预测一个宽平稳的随机过程。

$$Z(k)$$

  我们现在有P个数据，全部都发生在k时刻之前，我们希望用这P个数据去预测k时刻的值

$$Z(k)\leftarrow Z(k-1),...,Z(k-P)$$

  预测的方法是对这P个数据进行线性组合。

$$\sum _{m=1}^P{\alpha }_{m}Z(k-m)$$

  我们假设线性的系数已经是最优的了

$${\alpha }_1,..,{\alpha }_P=argmi{n}_{\alpha }E|Z(k)-\sum _{m=1}^P{\alpha }_{m}Z(k-m){|}^2$$

$${ϵ}_P=Z(k)-\sum _{m=1}^P{\alpha }_{m}Z(k-m)$$

  这个方程的求解之前介绍过,通过levension迭代可以解这个wiener hopf方程

$$\begin{gathered} \text{ Wiener Hopf} \\ {R}_Z\alpha =r \end{gathered}$$

  一般来说，随着P的增加，估计的误差会不断减小。但是我们想知道，随着P的无穷增加，误差会不会存在一个极限。我们之前探讨过使用Cramér–Rao来判断估计问题的极限，不过这里是线性估计问题，下界可能会有所差异

$$\begin{gathered} E|{ϵ}_P{|}^2={\sigma }_P^2 \\ {\sigma }_P^2\ge {\sigma }_{P+1}^2\ge ...\underrightarrow{P\to \infty }{\sigma }_{\infty }^2 \end{gathered}$$

  我们现在希望能够在有限的条件下，找到这个估计的下界。

  这个估计的下界是存在的，我们先说结论

$$\text{kolmogorov-Szago Identity}{\sigma }_{\infty }^2=exp(\frac{1}{2\pi }{\int }_{-\pi }^{\pi }log(S_Z(\omega ))d\omega )$$

  其中S_Z(ω)是Z(k)的功率谱密度

1.2 公式解读

  我们可以发现，估计的下界与功率谱有关系。因此，我们一旦知道了一个随机过程的功率谱密度，我们就能够知道预测可以做到怎么样的地步

  为什么预测会与功率谱密度相关呢

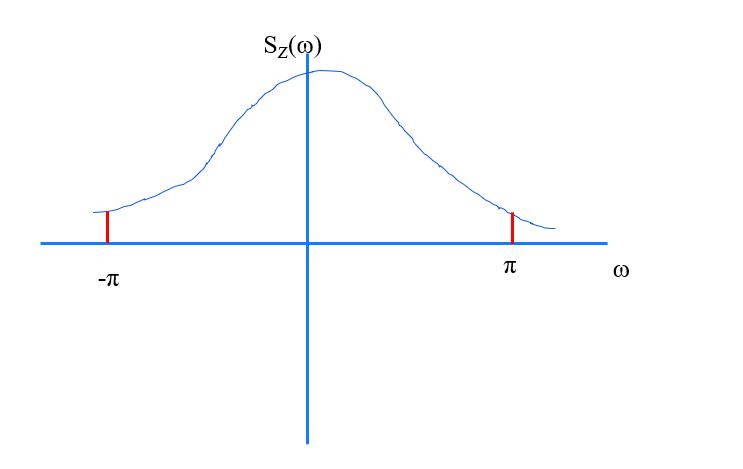
  假设功率谱密度比较集中在零点附近，log之后，对功率谱做积分，会得到负值非常大的数字，积分就会趋近于负无穷，取指数之后，就接近与0。说明我们能够很准确的预测。这是因为，如果功率谱比较集中，相关函数就会比较发散，比较胖。就说明不同时刻随机过程的取值，相关度比较高，说明数据之间具有密切的关系，预测就比较好做

  这里加一些自己的注解。因为相关函数和功率谱是傅里叶变换对的关系，相关函数是时域，功率谱是频域。如果功率谱比较集中，极端的看就是频谱上只有有限的几根线，时域上就是个标准的正弦函数曲线的叠加。因为相关函数是两个时间差的函数，一旦时域是无限长的函数，就说明任意两个时刻的点都具有相关性。相关性一旦强了，预测就好做

  反之，我们知道，如果功率谱很宽，积分会收敛，指数值就能够求出来，就说明误差就会有下界。因为功率谱一旦宽了，相关函数就会比较密集，不同时刻的相关度就会比较低。既然数据相关性不大，那么预测也难做。

1.3 白噪声的预测误差分析

  我们以白噪声为例，白噪声的功率谱是个常数。我们求解一下误差下界的这个式子，最后求出来的结果就是功率谱密度

$$\begin{gathered} \text{White Noise}{\sigma }_{\infty }^P=exp(\frac{1}{2\pi }{\int }_{-\pi }^{\pi }log(S_Z(\omega ))d\omega ) \\ =exp(\frac{1}{2\pi }{\int }_{-\pi }^{\pi }log(C)d\omega ) \\ =C=S_Z(\omega ) \end{gathered}$$

  再来看一下相关函数，如果功率谱密度是常数，则相关函数的这个积分，只有t=0的时候有值

$$\begin{gathered} R_Z(\tau )=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }{S}_Z(\omega )exp(j\omega \tau )d\omega \\ {R}_Z(\tau )=C\delta (\tau ) \\ {R}_Z(0)=C \end{gathered}$$

  因此

$${\sigma }_{\infty }^{}$$

现代信号处理 06 - 卡尔曼滤波

随机过程19 - 随机过程的线性预测问题

随机过程的线性预测

随机过程19 - 随机过程的线性预测问题

随机过程19 - 随机过程的线性预测问题