（回溯法）Java 求解分割回文串

Posted 2021-12-28 南淮北安

文章目录

• • 一、题目
  • 二、回溯法分析
  • 三、代码
  • 四、动态规划分析
  • 五、总结

一、题目

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是 回文串 。返回 s 所有可能的分割方案。

回文串 是正着读和反着读都一样的字符串。

二、回溯法分析

本题需要解决两个问题：

（1）切割问题，有不同的切割方式
（2）判断回文

其实切割问题，类似组合问题

例如对于字符串abcd
组合问题：选取一个a之后，在bcd中再去选取第二个，选取b之后在cd中在选取第三个…
切割问题：切割一个a之后，在bcd中再去切割第二段，切割b之后在cd中在切割第三段…

所以切割问题也可以抽象为一颗树形结构：

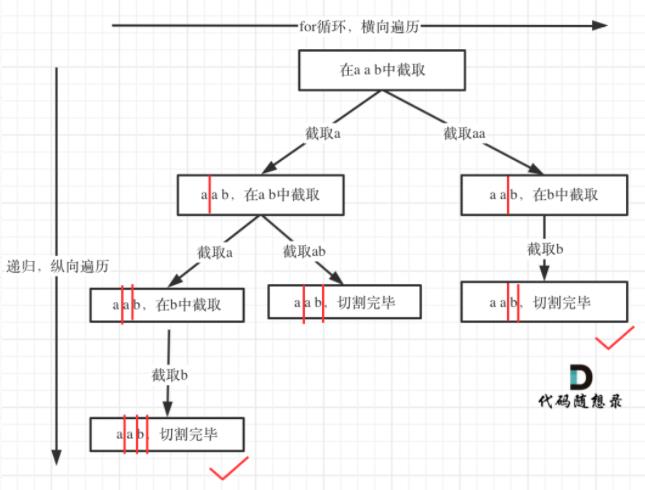
递归用来纵向遍历，for循环用来横向遍历，切割线（就是图中的红线）切割到字符串的结尾位置，说明找到了一个切割方法

所以这个切割过程和组合问题类似，也可以看成有多少种组合方式，判断这种组合方式符不符合要求，符合的话就记录。

（1）确定递归参数

首先字符串s，然后startIndex记录从哪一位开始，防止重复

backTracking(s, 0);

（2）确定递归终止条件

当startIndex遍历到字符串s末尾时，表示这趟遍历结束，记录数据

if (startIndex >= s.length()) 
    lists.add(new ArrayList(deque));
    return;

（3）确定回溯搜索过程

startIndex表示下一轮递归遍历的起始位置，也可以看作切割线
在for (int i = startIndex; i < s.length(); i++)循环中，我们 定义了起始位置startIndex，那么 [startIndex, i] 就是要截取的子串
判断这个子串是否是回文子串，如果是记录

三、代码

class Solution 
    List<List<String>> lists = new ArrayList<>();
    Deque<String> deque = new LinkedList<>();

    public List<List<String>> partition(String s) 
        backTracking(s, 0);
        return lists;
    

    private void backTracking(String s, int startIndex) 
        //如果起始位置大于s的大小，说明找到了一组分割方案
        if (startIndex >= s.length()) 
            lists.add(new ArrayList(deque));
            return;
        
        for (int i = startIndex; i < s.length(); i++) 
            //如果是回文子串，则记录
            if (isPalindrome(s, startIndex, i)) 
                String str = s.substring(startIndex, i + 1);
                deque.addLast(str);
             else 
                continue;
            
            //起始位置后移，保证不重复
            backTracking(s, i + 1);
            deque.removeLast();
        
    
    //判断是否是回文串
    private boolean isPalindrome(String s, int startIndex, int end) 
        for (int i = startIndex, j = end; i < j; i++, j--) 
            if (s.charAt(i) != s.charAt(j)) 
                return false;
            
        
        return true;
    

public class Main
    public static void main(String[] args) 
        Solution solution = new Solution();
        solution.partition("cdd");
    

四、动态规划分析

该题也可以先判断字符串中的回文串，然后回溯搜索时，直接使用判断结果即可

（1）确定dp数组及下标含义

boolean dp[i][j] 表示字符串i下标到j下标是否为回文串

（2）确定递推表达式

对于dp[i][j]的结果，由三种情况判断，当s.charAt(i)==s.charAt(j)时
第一种情况：如果 j-i=0 表示单位字符，比如 a ，则 dp[i][j]=true;
第二种情况：如果 j-i=1 表示单位字符，比如 aa ，则 dp[i][j]=true;
第三种情况：如果 j-i>1 ，则如果dp[i+1][j-1] 为 true，则 dp[i][j]=true;

（3）确定dp数组初始化

初始均为 false

（4）确定遍历顺序

由 dp[i][j] 由 dp[i+1][j-1] 决定，所以 i 需要降序，j 需要升序

public List<List<String>> partition(String s) 
        boolean[][] dp = new boolean[s.length()][s.length()];
        for (int i = s.length()-1; i >=0; i--) 
            for (int j = i; j < s.length(); j++) 
                if (s.charAt(i)==s.charAt(j))
                    if (j-i<=1)
                        dp[i][j]=true;
                    else if (dp[i+1][j-1])
                        dp[i][j]=true;
                    
                
            

        
        backTracking(dp,s, 0);
        System.out.println(lists.toString());
        return lists;
    

    private void backTracking(boolean[][] dp,String s, int startIndex) 
        //如果起始位置大于s的大小，说明找到了一组分割方案
        if (startIndex >= s.length()) 
            lists.add(new ArrayList(deque));
            return;
        
        for (int i = startIndex; i < s.length(); i++) 
            //如果是回文子串，则记录
            if (dp[startIndex][i]) 
                String str = s.substring(startIndex, i + 1);
                deque.addLast(str);
             else 
                continue;
            
            //起始位置后移，保证不重复
            backTracking(dp,s, i + 1);
            deque.removeLast();
        
    

五、总结

分割问题，类似组合问题，需要找出所有的情况，然后判定每种情况是否符合，所以选择回溯法进行解决，

对于回文串的判断，可以借助动态规划解决。