cf D. Not Quite Lee

Posted 2021-12-24 yeah17981

传送门：Problem - D - Codeforces

大意：给一个数组b，求子序列c是“good”个数，一个“good”的序列满足c1，c2，……，cn构造n个数字串，第i串有ci个数字，且为连续数字（like：-1，0，1，2），使得n个数字串中的数字的和为0

第一步：如何判断一个序列是否满足条件。我们假定ci构造出来的数字串是以xi开头的，那么就是xi-（xi+ci-1），sumi（ci的数字串的和）=（2*xi+ci-1）*ci/2=（ci-1）*ci/2+xi*ci

有解的时候sum1+sum2+……+sumi=0 因此 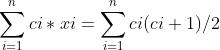时有解

由裴蜀定理得知，gcd（c1，c2……，cn）=g，则必有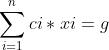，所以将问题转化为求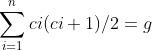是否有解

当g是奇数的时候，因为g是ci的因数，且g是奇数，所以g一定是ci/2的因数，且ci*（ci+1）/2一定是g的倍数，所以一定有解

当g为偶数的时候，设g%（2^l）=k（k为奇数），同理，k一定是ci/2的因数，因此问题转化为判断2^l是否为ci*（ci+1）/2的因数

首先2^l一定是ci的因数，此时分成2^l是与不是ci/2的因数的两种情况

2^l是ci/2的因数，则有解

2^l不是ci/2的因数，如果将所有的这类情况统计下来是偶数的话也能凑成解，没有就无了

第二步：预处理每个ci的l，并且统计每个l对应多少个ci

第三步，枚举每个l，找到此时能被2^l和2^(l+1)整除的ci的个数x,y。因此现在有2^x个序列（包括空序列）能使 2^l被g整除，但其中可能有奇数个元素不能被2^（l+1）整除的，这种情况数占总数的一半。如果序列中的每个ci都能被2^（l+1）整除，有2^y种方案，则会重复计算，于是删去，所以每个l的结果是2^（x+1）-2^y

结束

代码可见cf里的题解

Codeforces Global Round 17 Editorial - Codeforces