回归预测基于matlab Logistic混沌映射改进的麻雀搜索算法优化BP神经网络回归预测含Matlab源码 1552期

Posted 2021-12-24 紫极神光

一、麻雀算法简介

麻雀搜索算法(Sparrow Search Algorithm, SSA)是于2020年提出的。SSA 主要是受麻雀的觅食行为和反捕食行为的启发而提出的。该算法比较新颖，具有寻优能力强，收敛速度快的优点。
1 算法原理
建立麻雀搜索算法的数学模型，主要规则如下所述：
（1）发现者通常拥有较高的能源储备并且在整个种群中负责搜索到具有丰富食物的区域，为所有的加入者提供觅食的区域和方向。在模型建立中能量储备的高低取决于麻雀个体所对应的适应度值(Fitness Value)的好坏。
（2）一旦麻雀发现了捕食者，个体开始发出鸣叫作为报警信号。当报警值大于安全值时，发现者会将加入者带到其它安全区域进行觅食。
（3）发现者和加入者的身份是动态变化的。只要能够寻找到更好的食物来源，每只麻雀都可以成为发现者，但是发现者和加入者所占整个种群数量的比重是不变的。也就是说，有一只麻雀变成发现者必然有另一只麻雀变成加入者。
（4）加入者的能量越低，它们在整个种群中所处的觅食位置就越差。一些饥肠辘辘的加入者更有可能飞往其它地方觅食，以获得更多的能量。
（5）在觅食过程中，加入者总是能够搜索到提供最好食物的发现者，然后从最好的食物中获取食物或者在该发现者周围觅食。与此同时，一些加入者为了增加自己的捕食率可能会不断地监控发现者进而去争夺食物资源。
（6）当意识到危险时，群体边缘的麻雀会迅速向安全区域移动，以获得更好的位置，位于种群中间的麻雀则会随机走动，以靠近其它麻雀。
在模拟实验中，我们需要使用虚拟麻雀进行食物的寻找，由n只麻雀组成的种群可表示为如下形式：

其中，d表示待优化问题变量的维数，n则是麻雀的数量。那么，所有麻雀的适应度值可以表示为如下形式：

其中，f表示适应度值。
在SSA中， 具有较好适应度值的发现者在搜索过程中会优先获取食物。此外， 因为发现者负责为整个麻雀种群寻找食物并为所有加入者提供觅食的方向。因此，发现者可以获得比加入者更大的觅食搜索范围。根据规则(1)和规则(2)，在每次迭代的过程中，发现者的位置更新描述如下：

其中， t代表当前迭代数， j=1， 2， 3， …， d.item maz是一个常数，表示最大的迭代次数。Xy表示第i个麻雀在第j维中的位置信息。xE(0，1]是一个随机数。R2(R2E[0，1])和ST(STe[0.5， 1] ) 分别表示预警值和安全值。Q是服从正态分布的随机数.L表示一个1×d的矩阵， 其中该矩阵内每个元素全部为
1.
当R2<ST时，这意味着此时的觅食环境周围没有捕食者，发现者可以执行广泛的搜索操作。如果R2≥ST，这表示种群中的一些麻雀已经发现了捕食者，井向种群中其它麻雀发出了警报，此时所有麻雀都需要迅速飞到其它安全的地方进行觅食。对于加入者，它们需要执行规则(3)和规则(4)。如前面所描述，在觅食过程中，一些加入者会时刻监视着发现者。一旦它们察觉到发现者已经找到了更好的食物，它们会立即离开现在的位置去争夺食物。如果它们赢了，它们可以立即获得该发现者的食物，否则需要继续执行规则(4)。加入者的位置更新描述如下：

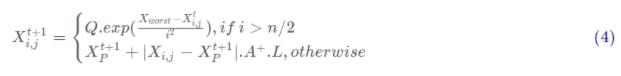
其中， X， 是目前发现者所占据的最优位置， X worst则表示当前全局最差的位置。A表示一个1×d的矩阵， 其中每个元素随机赋值为1或-1，并且A+=A(AA)-.当i>n/2时，这表明，适应度值较低的第i个加入者没有获得食物，处于十分饥饿的状态，此时需要飞往其它地方觅食，以获得更多的能量。在模拟实验中，我们假设这些意识到危险的麻雀占总数量的10%到20%。这些麻雀的初始位置是在种群中随机产生的。根据规则(5)，其数学表达式可以表示为如下形式：

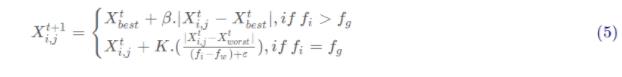
其中， 其中X best是当前的全局最优位置。β作为步长控制参数， 是服从均值为0， 方差为1的正态分布的随机数。KE[-1， 1] 是一个随机数，则是当前麻雀个体的适应度值。f，和fw分别是当前全局最佳和最差的适应度值。e的常数，以避免分母出现零。
为简单起见， 当f：>f， 表示此时的麻雀正处于种群的边缘， 极其容易受到捕食者的攻击。X best表示这个位置的麻雀是种群中最好的位置也是十分安全的。f；=f，时，这表明处于种群中间的麻雀意识到了危险，需要靠近其它的麻雀以此尽量减少它们被捕食的风险。K表示麻雀移动的方向同时也是步长控制参数。

2 算法流程

Step1： 初始化种群，迭代次数，初始化捕食者和加入者比列。
Step2：计算适应度值，并排序。
Step3：利用式（3）更新捕食者位置。
Step4：利用式（4）更新加入者位置。
Step5：利用式（5）更新警戒者位置。
Step6：计算适应度值并更新麻雀位置。
Step7：是否满足停止条件，满足则退出，输出结果，否则，重复执行Step2-6；

二、BP神经网络简介

1 BP神经网络概述
BP（Back Propagation）神经网络是1986年由Rumelhart和McCelland为首的科研小组提出，参见他们发表在Nature上的论文 Learning representations by back-propagating errors 。
BP神经网络是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。BP网络能学习和存贮大量的 输入-输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法，通过反向传播来不断 调整网络的权值和阈值，使网络的误差平方和最小。

2 BP算法的基本思想
上一次我们说到，多层感知器在如何获取隐层的权值的问题上遇到了瓶颈。既然我们无法直接得到隐层的权值，能否先通过输出层得到输出结果和期望输出的误差来间接调整隐层的权值呢？BP算法就是采用这样的思想设计出来的算法，它的基本思想是,学习过程由信号的正向传播与误差的反向传播两个过程组成。
正向传播时，输入样本从输入层传入,经各隐层逐层处理后,传向输出层。若输出层的实际输出与期望的输出(教师信号)不符,则转入误差的反向传播阶段。
反向传播时，将输出以某种形式通过隐层向输入层逐层反传,并将误差分摊给各层的所有单元,从而获得各层单元的误差信号,此误差信号即作为修正各单元权值的依据。这两个过程的具体流程会在后文介绍。

BP算法的信号流向图如下图所示

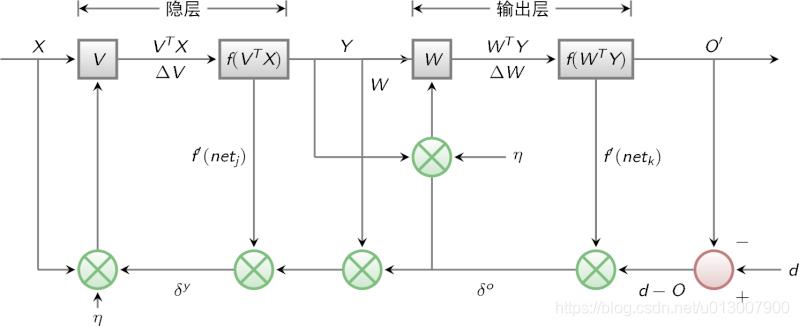
3 BP网络特性分析——BP三要素
我们分析一个ANN时，通常都是从它的三要素入手，即
1)网络拓扑结构；
2)传递函数；
3)学习算法。

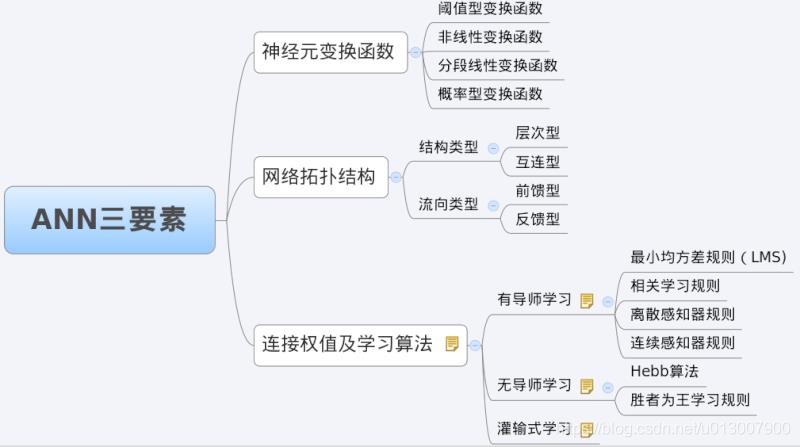
每一个要素的特性加起来就决定了这个ANN的功能特性。所以，我们也从这三要素入手对BP网络的研究。

3.1 BP网络的拓扑结构
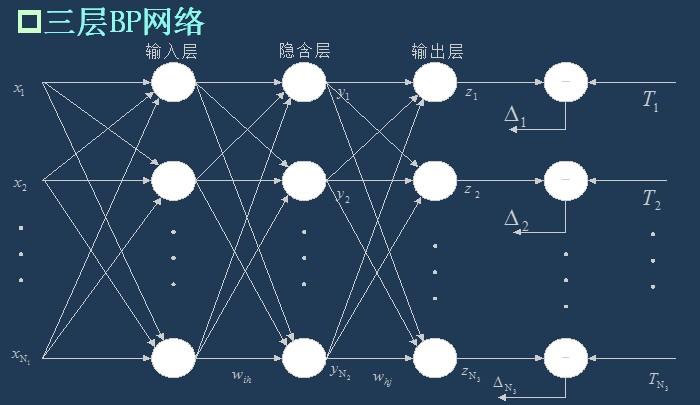
上一次已经说了，BP网络实际上就是多层感知器，因此它的拓扑结构和多层感知器的拓扑结构相同。由于单隐层（三层）感知器已经能够解决简单的非线性问题，因此应用最为普遍。三层感知器的拓扑结构如下图所示。
一个最简单的三层BP：

3.2 BP网络的传递函数
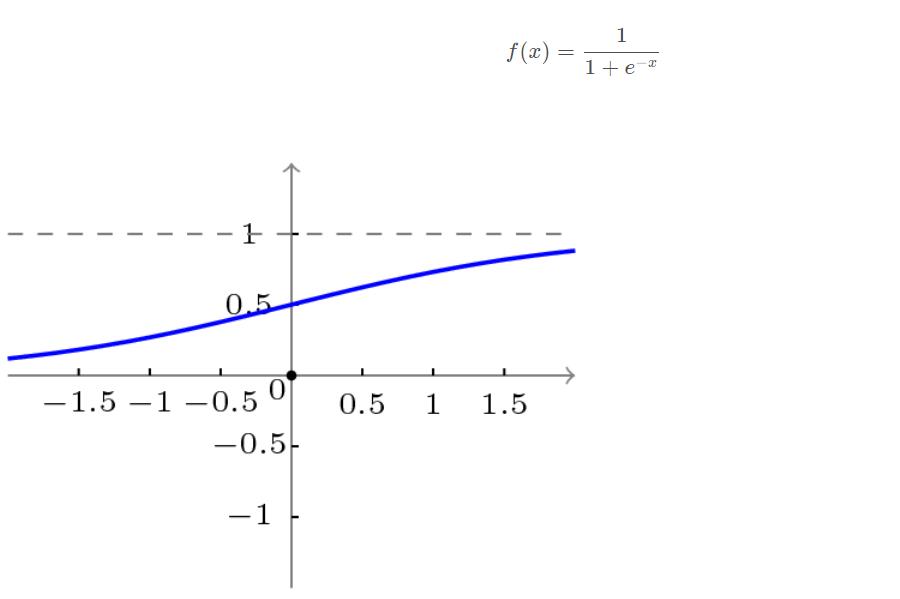
BP网络采用的传递函数是非线性变换函数——Sigmoid函数（又称S函数）。其特点是函数本身及其导数都是连续的，因而在处理上十分方便。为什么要选择这个函数，等下在介绍BP网络的学习算法的时候会进行进一步的介绍。
单极性S型函数曲线如下图所示。

双极性S型函数曲线如下图所示。

3.3 BP网络的学习算法
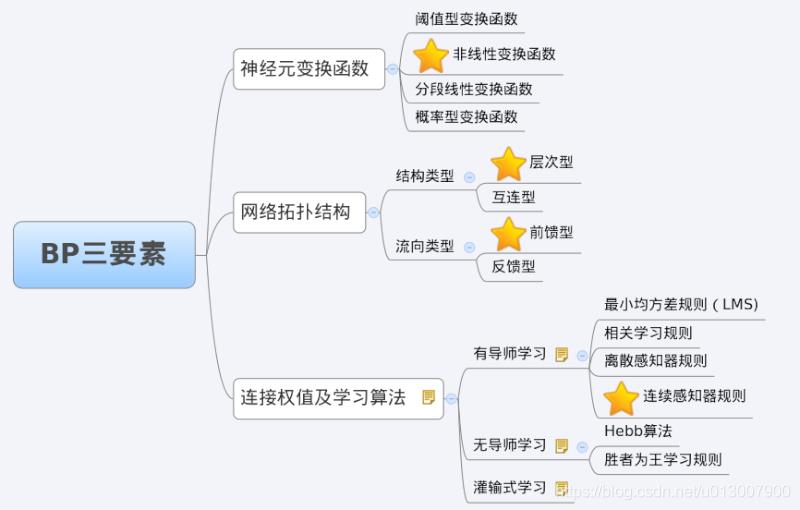
BP网络的学习算法就是BP算法，又叫 δ 算法（在ANN的学习过程中我们会发现不少具有多个名称的术语）， 以三层感知器为例，当网络输出与期望输出不等时，存在输出误差 E ，定义如下




下面我们会介绍BP网络的学习训练的具体过程。

4 BP网络的训练分解
训练一个BP神经网络，实际上就是调整网络的权重和偏置这两个参数，BP神经网络的训练过程分两部分：

前向传输，逐层波浪式的传递输出值；
逆向反馈，反向逐层调整权重和偏置；
我们先来看前向传输。
前向传输（Feed-Forward前向反馈）
在训练网络之前，我们需要随机初始化权重和偏置，对每一个权重取[ − 1 , 1 ] [-1,1][−1,1]的一个随机实数，每一个偏置取[ 0 , 1 ] [0,1][0,1]的一个随机实数，之后就开始进行前向传输。

神经网络的训练是由多趟迭代完成的，每一趟迭代都使用训练集的所有记录，而每一次训练网络只使用一条记录，抽象的描述如下：

while 终止条件未满足：
    for record:dataset:
        trainModel(record)

4.1 逆向反馈（Backpropagation）


4.2 训练终止条件
每一轮训练都使用数据集的所有记录，但什么时候停止，停止条件有下面两种：
设置最大迭代次数，比如使用数据集迭代100次后停止训练
计算训练集在网络上的预测准确率，达到一定门限值后停止训练

5 BP网络运行的具体流程
5.1 网络结构
输入层有n nn个神经元，隐含层有p pp个神经元，输出层有q qq个神经元。

5.2 变量定义








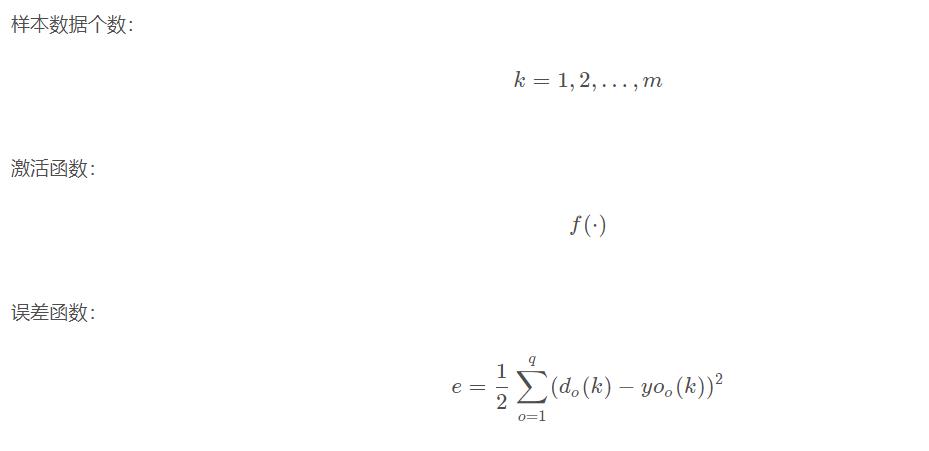
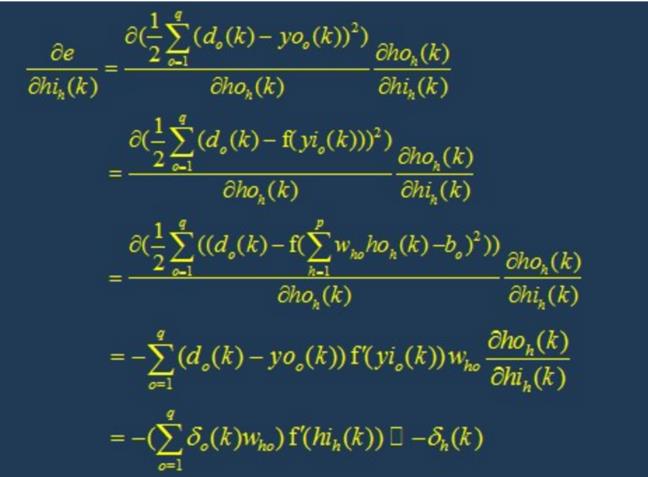
第九步：判断模型合理性
判断网络误差是否满足要求。
当误差达到预设精度或者学习次数大于设计的最大次数，则结束算法。
否则，选取下一个学习样本以及对应的输出期望，返回第三部，进入下一轮学习。

6 BP网络的设计
在进行BP网络的设计是，一般应从网络的层数、每层中的神经元个数和激活函数、初始值以及学习速率等几个方面来进行考虑，下面是一些选取的原则。

6.1 网络的层数
理论已经证明，具有偏差和至少一个S型隐层加上一个线性输出层的网络，能够逼近任何有理函数，增加层数可以进一步降低误差，提高精度，但同时也是网络 复杂化。另外不能用仅具有非线性激活函数的单层网络来解决问题，因为能用单层网络解决的问题，用自适应线性网络也一定能解决，而且自适应线性网络的 运算速度更快，而对于只能用非线性函数解决的问题，单层精度又不够高，也只有增加层数才能达到期望的结果。

6.2 隐层神经元的个数
网络训练精度的提高，可以通过采用一个隐含层，而增加其神经元个数的方法来获得，这在结构实现上要比增加网络层数简单得多。一般而言，我们用精度和 训练网络的时间来恒量一个神经网络设计的好坏：
（1）神经元数太少时，网络不能很好的学习，训练迭代的次数也比较多，训练精度也不高。
（2）神经元数太多时，网络的功能越强大，精确度也更高，训练迭代的次数也大，可能会出现过拟合(over fitting)现象。
由此，我们得到神经网络隐层神经元个数的选取原则是：在能够解决问题的前提下，再加上一两个神经元，以加快误差下降速度即可。

6.3 初始权值的选取
一般初始权值是取值在(−1,1)之间的随机数。另外威得罗等人在分析了两层网络是如何对一个函数进行训练后，提出选择初始权值量级为s√r的策略， 其中r为输入个数，s为第一层神经元个数。

6.4 学习速率
学习速率一般选取为0.01−0.8，大的学习速率可能导致系统的不稳定，但小的学习速率导致收敛太慢，需要较长的训练时间。对于较复杂的网络， 在误差曲面的不同位置可能需要不同的学习速率，为了减少寻找学习速率的训练次数及时间，比较合适的方法是采用变化的自适应学习速率，使网络在 不同的阶段设置不同大小的学习速率。

6.5 期望误差的选取
在设计网络的过程中，期望误差值也应当通过对比训练后确定一个合适的值，这个合适的值是相对于所需要的隐层节点数来确定的。一般情况下，可以同时对两个不同 的期望误差值的网络进行训练，最后通过综合因素来确定其中一个网络。

7 BP网络的局限性
BP网络具有以下的几个问题：
(1)需要较长的训练时间：这主要是由于学习速率太小所造成的，可采用变化的或自适应的学习速率来加以改进。
(2)完全不能训练：这主要表现在网络的麻痹上，通常为了避免这种情况的产生，一是选取较小的初始权值，而是采用较小的学习速率。
(3)局部最小值：这里采用的梯度下降法可能收敛到局部最小值，采用多层网络或较多的神经元，有可能得到更好的结果。

8 BP网络的改进
P算法改进的主要目标是加快训练速度，避免陷入局部极小值等，常见的改进方法有带动量因子算法、自适应学习速率、变化的学习速率以及作用函数后缩法等。 动量因子法的基本思想是在反向传播的基础上，在每一个权值的变化上加上一项正比于前次权值变化的值，并根据反向传播法来产生新的权值变化。而自适应学习 速率的方法则是针对一些特定的问题的。改变学习速率的方法的原则是，若连续几次迭代中，若目标函数对某个权倒数的符号相同，则这个权的学习速率增加， 反之若符号相反则减小它的学习速率。而作用函数后缩法则是将作用函数进行平移，即加上一个常数。

三、部分源代码

%% 初始化
clear
close all
clc
warning off

%% 数据读取
data=xlsread('数据.xlsx','Sheet1','A1:N252'); %%使用xlsread函数读取EXCEL中对应范围的数据即可

%输入输出数据
input=data(:,1:end-1);    %data的第一列-倒数第二列为特征指标
output=data(:,end);  %data的最后面一列为输出的指标值

N=length(output);   %全部样本数目
testNum=15;   %设定测试样本数目
trainNum=N-testNum;    %计算训练样本数目

%% 划分训练集、测试集
input_train = input(1:trainNum,:)';
output_train =output(1:trainNum)';
input_test =input(trainNum+1:trainNum+testNum,:)';
output_test =output(trainNum+1:trainNum+testNum)';

%% 数据归一化
[inputn,inputps]=mapminmax(input_train,0,1);
[outputn,outputps]=mapminmax(output_train);
inputn_test=mapminmax('apply',input_test,inputps);

%% 获取输入层节点、输出层节点个数
inputnum=size(input,2);
outputnum=size(output,2);
disp('/')
disp('神经网络结构...')
disp(['输入层的节点数为：',num2str(inputnum)])
disp(['输出层的节点数为：',num2str(outputnum)])
disp(' ')
disp('隐含层节点的确定过程...')

%确定隐含层节点个数
%采用经验公式hiddennum=sqrt(m+n)+a，m为输入层节点个数，n为输出层节点个数，a一般取为1-10之间的整数
MSE=1e+5; %初始化最小误差
for hiddennum=fix(sqrt(inputnum+outputnum))+1:fix(sqrt(inputnum+outputnum))+10
    
    %构建网络
    net=newff(inputn,outputn,hiddennum);
    % 网络参数
    net.trainParam.epochs=1000;         % 训练次数
    net.trainParam.lr=0.01;                   % 学习速率
    net.trainParam.goal=0.000001;        % 训练目标最小误差
    % 网络训练
    net=train(net,inputn,outputn);
    an0=sim(net,inputn);  %仿真结果
    mse0=mse(outputn,an0);  %仿真的均方误差
    disp(['隐含层节点数为',num2str(hiddennum),'时，训练集的均方误差为：',num2str(mse0)])
    
    %更新最佳的隐含层节点
    if mse0<MSE
        MSE=mse0;
        hiddennum_best=hiddennum;
    end
end
function error = fitness(x,inputnum,hiddennum_best,outputnum,net,inputn,outputn,output_train,inputn_test,outputps,output_test)
%该函数用来计算适应度值
hiddennum=hiddennum_best;
%提取
setdemorandstream(pi);   

w1=x(1:inputnum*hiddennum);%取到输入层与隐含层连接的权值
B1=x(inputnum*hiddennum+1:inputnum*hiddennum+hiddennum);%隐含层神经元阈值
w2=x(inputnum*hiddennum+hiddennum+1:inputnum*hiddennum+hiddennum+hiddennum*outputnum);%取到隐含层与输出层连接的权值
B2=x(inputnum*hiddennum+hiddennum+hiddennum*outputnum+1:inputnum*hiddennum+hiddennum+hiddennum*outputnum+outputnum);%输出层神经元阈值

net.trainParam.showWindow=0;  %隐藏仿真界面

%网络权值赋值
net.iw1,1=reshape(w1,hiddennum,inputnum);%将w1由1行inputnum*hiddennum列转为hiddennum行inputnum列的二维矩阵
net.lw2,1=reshape(w2,outputnum,hiddennum);%更改矩阵的保存格式
net.b1=reshape(B1,hiddennum,1);%1行hiddennum列，为隐含层的神经元阈值
net.b2=reshape(B2,outputnum,1);

%网络训练
net=train(net,inputn,outputn);

an0=sim(net,inputn);
train_simu=mapminmax('reverse',an0,outputps);
an=sim(net,inputn_test);
test_simu=mapminmax('reverse',an,outputps);

% error=mse(output_test,test_simu);   %适应度函数选取为测试集的均方误差，适应度函数值越小，表明模型的预测精度越高，注意newff函数搭建的BP，产生了交叉验证，因此选另外的数据预测误差作为适应度函数是合理。
error=(mse(output_train,train_simu)+mse(output_test,test_simu))/2; %适应度函数选取为训练集与测试集整体的均方误差平均值，适应度函数值越小，表明训练越准确，且兼顾模型的预测精度更好。

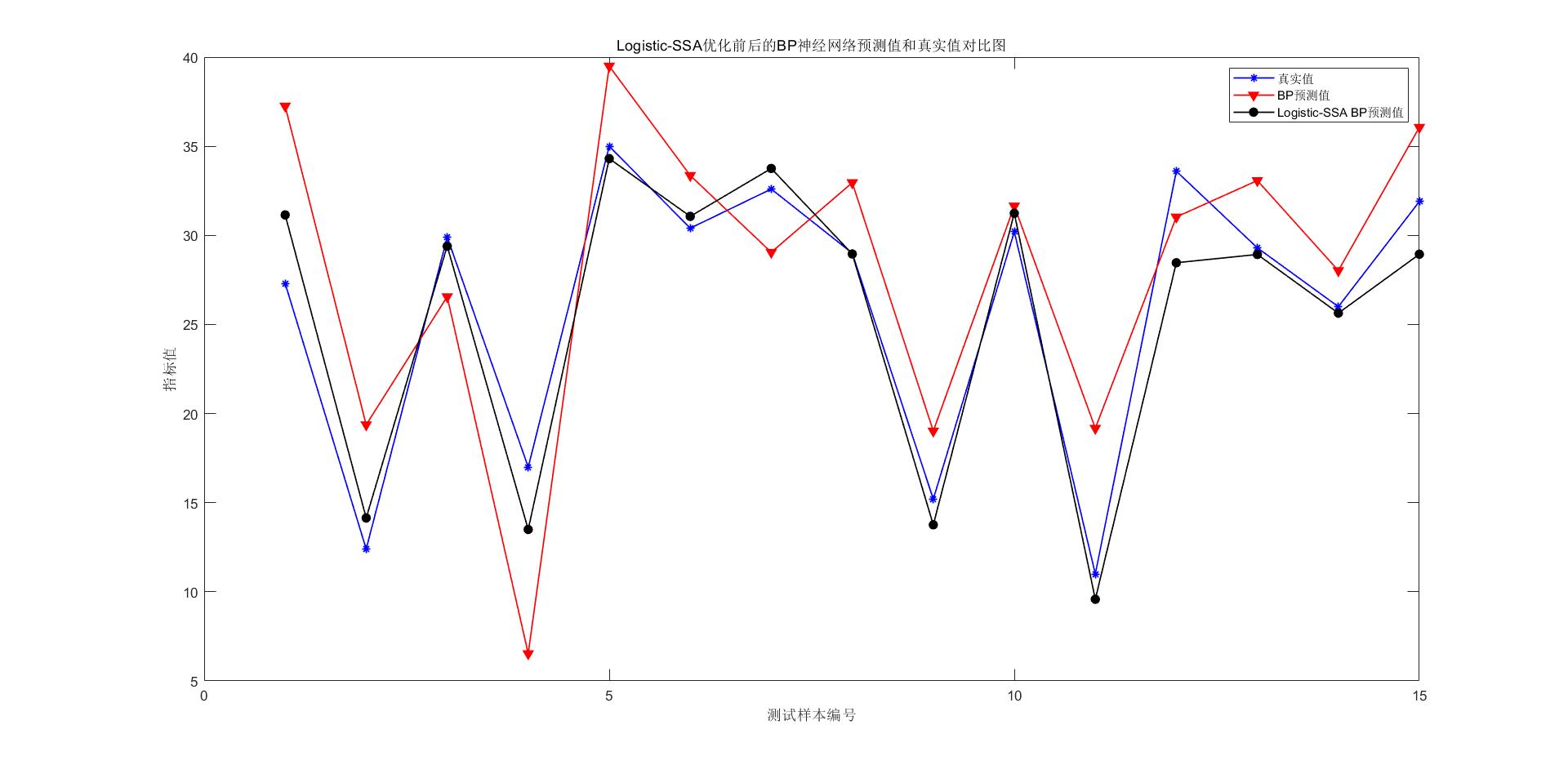
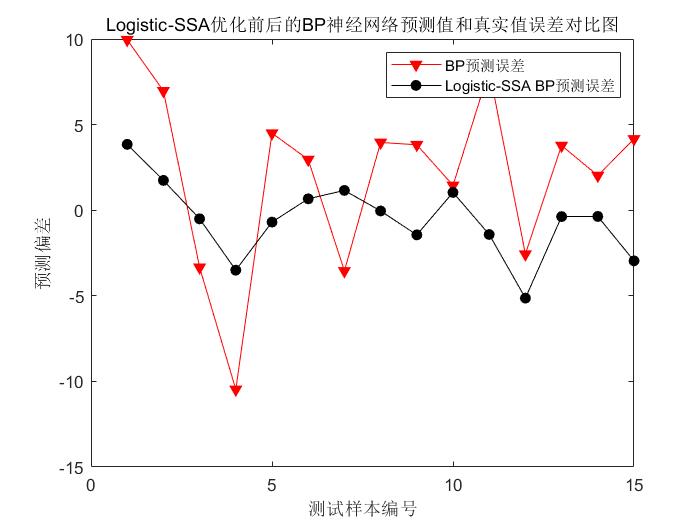
四、运行结果

五、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]周品.MATLAB 神经网络设计与应用[M].清华大学出版社，2013.
[4]陈明.MATLAB神经网络原理与实例精解[M].清华大学出版社，2013.
[5]方清城.MATLAB R2016a神经网络设计与应用28个案例分析[M].清华大学出版社，2018.