针对连续动作的DQN

Posted 2021-12-24 UQI-LIUWJ

1 前言

        跟基于策略梯度的方法比起来，DQN在处理连续状态的问题中 是比较好的。（因为前者是计算Q-table，后者是计算Q-function。前者在状态空间连续的时候是很难计算的）。

        同时，DQN是比较容易训练的：在 DQN 里面，你只要能够估计出Q函数，就保证你一定可以找到一个比较好的策略。也就是你只要能够估计出Q函数，就保证你可以改进策略。而估计Q函数这件事情，是比较容易的，因为它就是一个回归问题。在回归问题里面， 你可以轻易地知道模型学习得是不是越来越好，只要看那个回归的损失有没有下降，你就知道说模型学习得好不好，所以估计Q函数相较于学习一个策略是比较容易的。

        但是，DQN也存在一些问题，最大的问题是它不太容易处理连续动作。假设动作是连续的，做 DQN 就会有困难。因为在做 DQN 里面一个很重要的一步是你要能够解这个优化问题。估计出 Q函数Q(s,a) 以后，必须要找到一个 a，它可以让 Q(s,a)最大

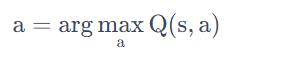
        假如a是连续的，你无法穷举所有可能的连续动作，来看哪一个连续动作可以让 Q 的值最大。

 

        那么，怎么解决这个问题呢？第八章 DQN (连续动作) (datawhalechina.github.io) 提出了四种方案：

2 方案1

        采样出 N 个可能的 a：，一个一个带到 Q函数里面，看那个最大。

        当然这不是一个非常精确的做法，因为你没有办法做太多的采样， 所以你估计出来的 Q 值，最后决定的动作可能不是非常的精确

3 方案2

        既然要解的是一个优化问题，那么我们要做的其实就是要最大化目标函数Q。

        要最大化一个东西， 就可以用梯度上升。

        我们就把a当作是参数，然后要找一组a去最大化Q函数，就用梯度上升去更新 a 的值，最后看看能不能找到一个a去最大化Q函数，也就是目标函数。

        但这种方案会遇到两个问题：

1）全局最大值的问题，我们可能会停在局部最大值， 就不见得能够真的找到最优的结果。

2）这个运算量会很大，因为我们需要迭代地训练Q函数和a的值。我们训练一个Q函数网络就很花时间了。如果你用梯度上升的方法来计算当前最优的a， 等于是你每次要决定采取哪一个动作的时候，都还要做一次训练网络的过程，显然运算量是很大的。

4 方案3

        第三个方案是特别设计一个网络的架构，或者说是特别设计Q函数，使得解 arg max 的问题变得非常容易。

        也就是说，这边的Q函数不是一个一般的Q函数，特别设计一下这个Q函数，是的Q函数最大的时候，a比较容易去求得。

        怎么去设计这个Q函数，是一个学问。（有些问题可能找不到这样的Q函数，或者Q函数不好找，这也是这一方案的局限性）下面举一个例子：

        输入 s，Q函数会输出 3 个东西。向量μ(s)，矩阵Σ(s)，标量V(s)。

        我们知道Q函数是需要输入一个状态s和一个动作a，然后决定一个值。我们现在只输入了s，还没有将a加进来。【这个例子里面a是机器人各个关节的旋转角度，也是一个向量】

        于是之后我们处理Q(s,a)，用a和μ(s)，Σ(s)，V一起计算最终的Q

        把向量 a 减掉向量μ，取转置，所以它是一个行向量。Σ 是一个矩阵。然后a减掉 μ(s) ，是一个列向量。所以是一个标量，这个数值就是 这个例子里面的Q(s,a)。

        假设 Q(s,a) 定义成这个样子，我们要怎么找到一个a去最大化这个 Q 值呢？这个方案非常简单。

        我们人为令Σ是一个正定矩阵（这个由的设计决定，它直接输出的不是正定矩阵，然后这个矩阵通过一些操作使它变成正定矩阵输入，称为Σ(s)）

        因而此时一定是正的，它前面乘上一个负号。所以第一项假设我们不看这个负号的话，第一项的值越小，最终的 Q 值就越大。

        怎么让第一项的值最小呢？直接把a代入 μ 的值，让它变成 0，就会让第一项的值最小。

5 方案4 

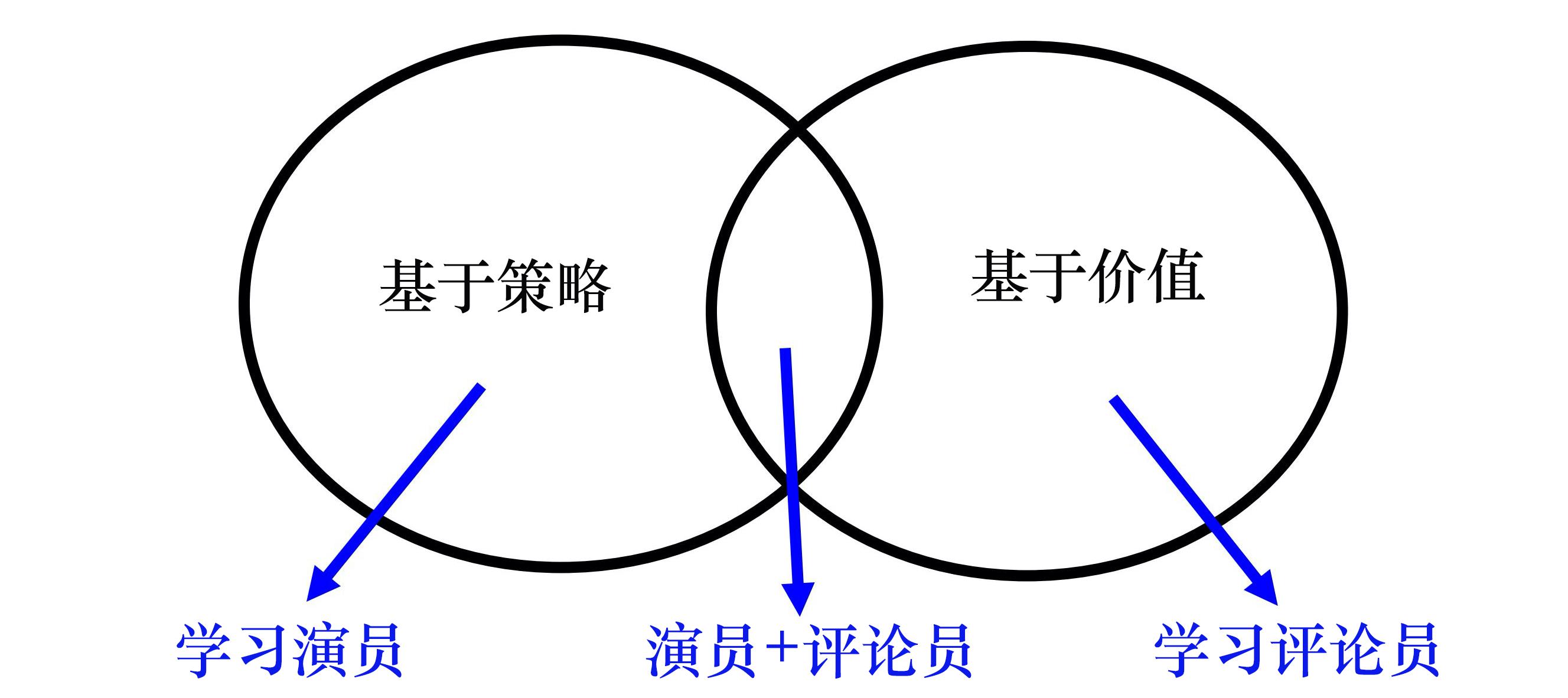
        第 4 种方案就是不要用 DQN。用 DQN 处理连续动作还是比较麻烦。 基于策略的方法 PPO 和基于价值的方法 DQN，这两者其实是可以结合在一起的，如下图所示，也就是演员-评论员的方法。