《数值分析》-- 牛顿插值

Posted 2021-12-24 胜天半月子

文章目录

• 问题
• 一、牛顿插值基函数
• 二、均差(差商)及其基本性质
• • 2.1 均差定义
  • 2.2 利用均差表计算均差 ⭐
  • 2.3 均差的性质
• 三、牛顿差值余项
• 习题

---

问题

一、牛顿插值基函数

Lagrange 插值虽然易算，但若要增加一个节点时，全部基函数$l_i(x)$都需要重新计算

• 牛顿插值基函数
  
  
• 确定系数$A_0,A_1,\dots ,A_n$
  依据插值条件(2),可以依次确定系数$A_0,A_1,\dots ,A_n$:
  
  
  
  
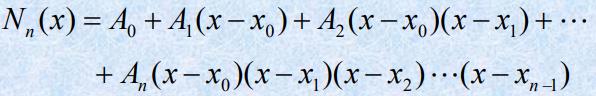
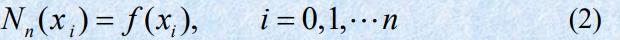
  即最后的系数：
  

---

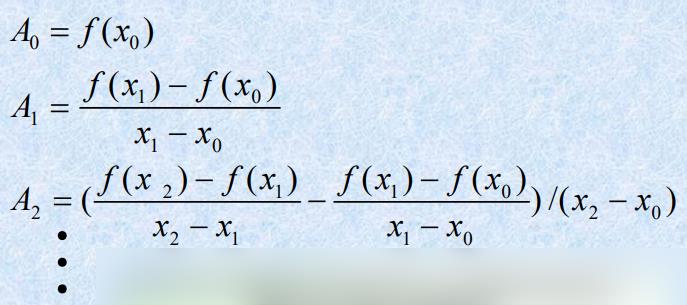
二、均差(差商)及其基本性质

2.1 均差定义

一阶均差的均差:


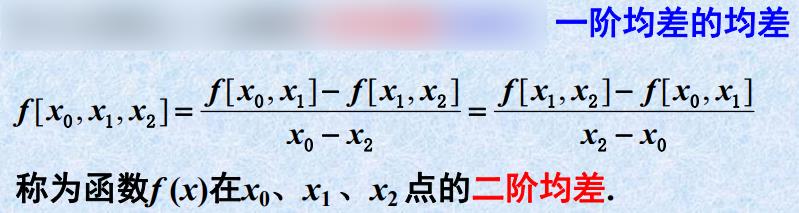
利用插值条件和均差的定义,可求出$N_n(x)$的系数$A_j$ :

2.2 利用均差表计算均差 ⭐

均差的计算步骤与结果可列成均差表，如下

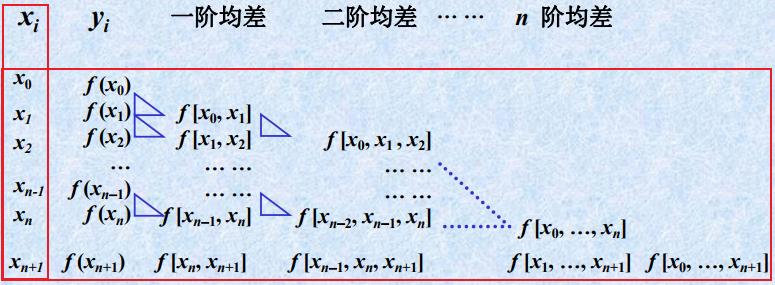
由均差定义可知：高阶均差是两个低一阶均差的均差。

习题

2.3 均差的性质

• 性质1：均差可以表示为函数值的线性组合
  
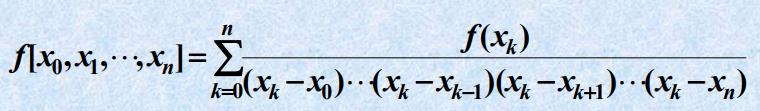
• 性质2（对称性）：均差的值与节点排列顺序无关
  
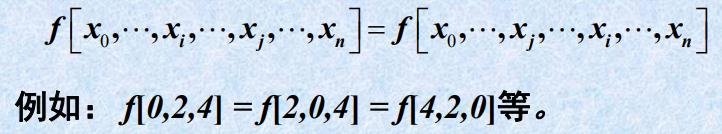
• 性质3 (均差与导数的关系)
  
• 性质4 (特征定理)
  
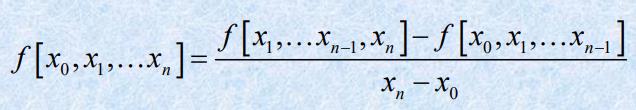
• 性质 5
  
• 牛顿插值多项式⭐
  
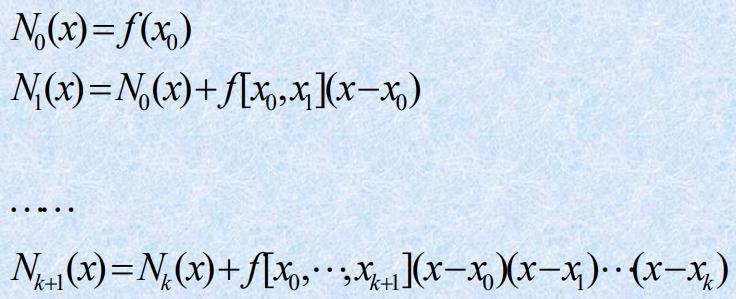
  每增加一个节点，Newton插值多项式只增加一项，克服了Lagrange插值的缺点。

---

三、牛顿差值余项

---

习题

• 例题

1. 已知信息$f(0)$=1,$f(-1)$=5,$f(2)$=-1,构造$f(x)$ 的均差表。
   

• 例题
  
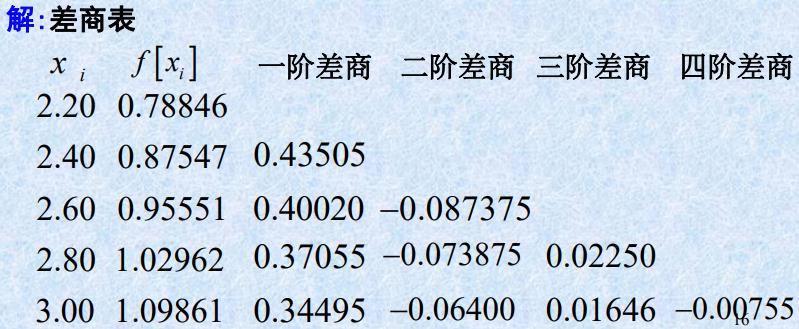
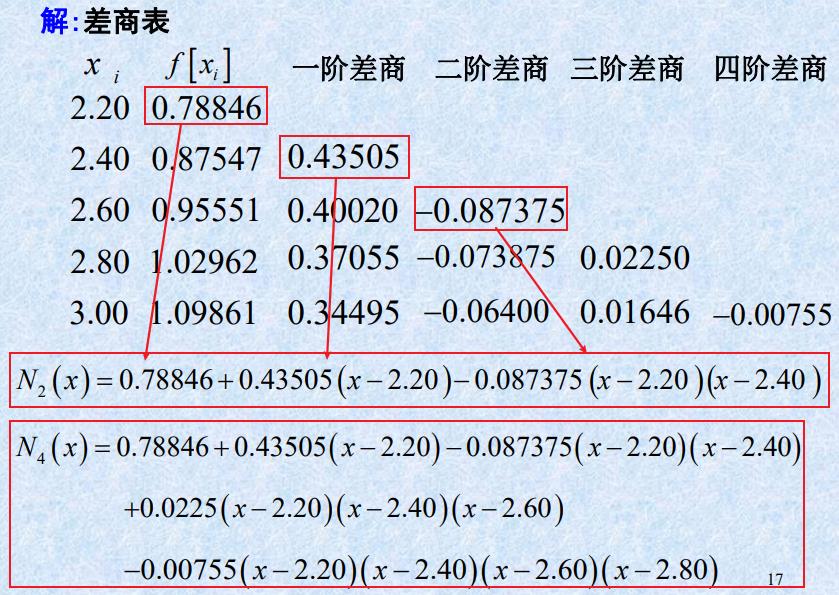
  1.构造差商表
  2.分别写出二次、四次Newton插值多项式
  
  
  
• 例题
  
  
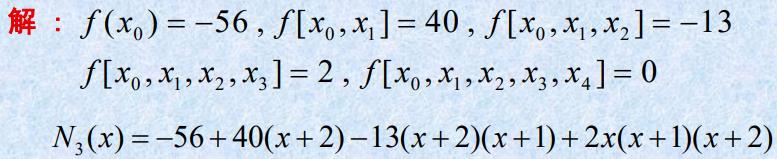
  详细计算过程：
  

---