数理统计均值检验（双侧单侧）和区间估计

Posted 2021-12-23 火柴先生

1区间估计是什么？

在统计推断中有两类问题，一类为估计问题，一类为假设检验。估计问题中主要包括点估计和区间估计，点估计是估计出一个分布中未知参数的值，区间估计则是估计出一个分布中未知参数所在的范围。

区间估计最终要估计出未知参数所在的区间，这个区间就是经常听到的置信区间

注意置信水平并非概率（如95%：我们有信心说（置信的意思），如果通过100次采样，采用同样的区间深度，得到100个置信区间，那么平均有95个包含μ）

2 均值检验

在区间估计中，当总体为正态分布时，常见的区间估计场景有以下几种。

2.1 方差已知，估计均值

U检验（Z检验）步骤

Z检验是一般用于大样本(即样本容量大于30)平均值差异性检验的方法（总体的方差已知）。它是用标准正态分布的理论来推断差异发生的概率，从而比较两个平均数的差异是否显著。

Z检验步骤：

第一步： 建立原假设 H0:μ = μ0 ，即先假定两个平均数之间没有显著差异

第二步： 计算统计量U(Z),对于不同类型的问题选用不同的统计量计算方法

• 如果检验一个样本平均数（X）与一个已知的总体平均数(μ0)的差异是否显著。其Z值计算公式为：

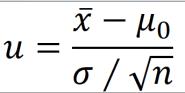
• 其中：X是检验样本的均值；μ0是已知总体均值；σ是总体的标准差；n是样本容量。

第三步：判断拒绝域

第四步：带入数据计算统计量，并判断是否落在拒绝域内，得出结论。

关于置信区间计算（通过下方截图，有助于理解）

2.2 方差未知，估计均值

• 用t检验
• 大样本（n>=30）,用u检验（z检验）

其他部分类似。

总结如下：

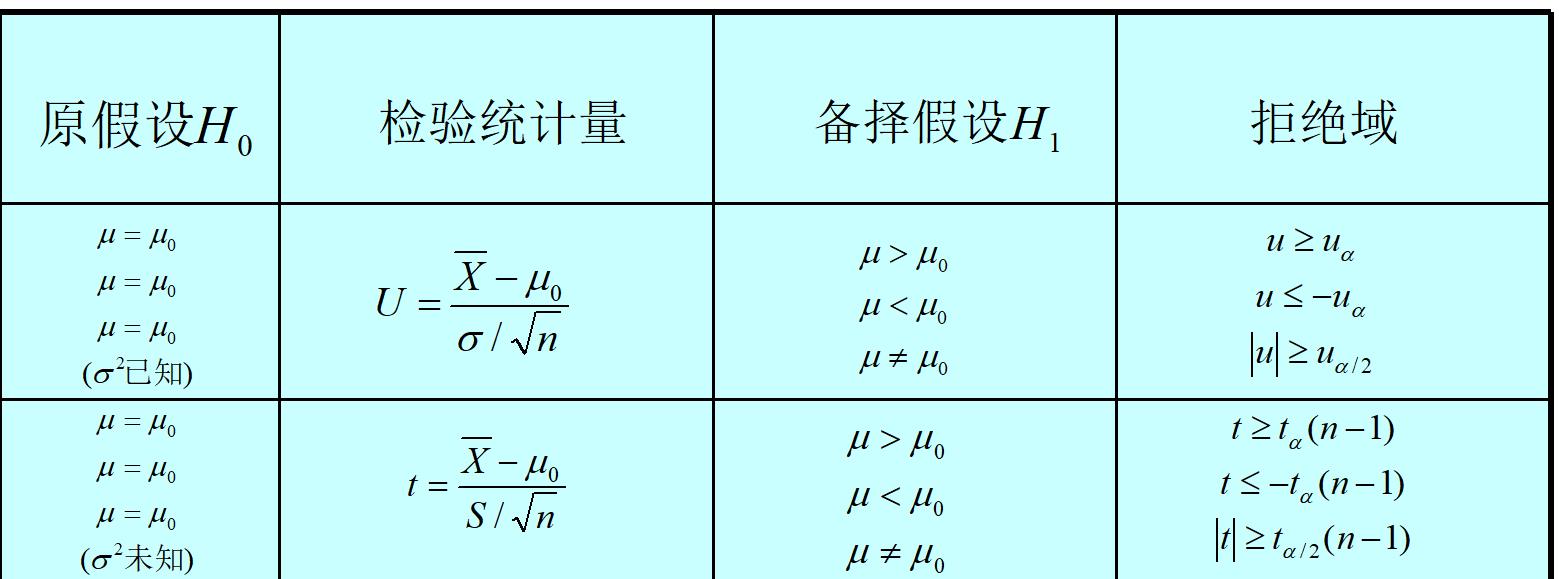
2.3 t检验与u检验区别

u检验和t检验可用于样本均数与总体均数的比较以及两样本均数的比较。

理论上要求样本来自正态分布总体。

但在实用时，只要满足大样本，或总体标准差σ已知 时，就可应用 u检验 ；

n小且总体标准差σ未知时 ，可应用 t检验 ，但要求样本来自正态分布总体。两样本均数比较时还要求两总体方差相等。

References

常用的假设检验方法(U检验、T检验、卡方检验、F检验