数据结构—图图的定义图的存储结构

Posted 2021-12-23 之墨_

数据结构—图

• 图的定义
• ADT Graph
• 有向图与无向图
• • 有向图
  • 无向图
• 图的基本术语
• • 端点和邻接点
  • 顶点的度、入度和出度
  • 完全图
  • 稠密图和稀疏图
  • 子图
  • 路径和路径长度
  • 连通、连通图、连通分量、可达
  • 强连通图和强连通分量
  • 权和网
• 图的存储结构
• • 邻接矩阵存储方法
  • 代码实现

图的定义

无论多么复杂的图都是由顶点和边构成的
采用形式化的定义
图(graph)G 由两个集合 **V(vertex)**和 E(edge)组成
记为 G=(V,E)
其中V 是顶点的有限集合,记为 V(G) E是连接 V 中两个不同顶点(顶点对)的边的有限集合,记为 E(G)

说明：
对于n个顶点的图，对每个顶点连续编号，即顶点的编号为0~n-1 通过编号唯一确定一个顶点

图是现实问题的抽象，例如七桥问题

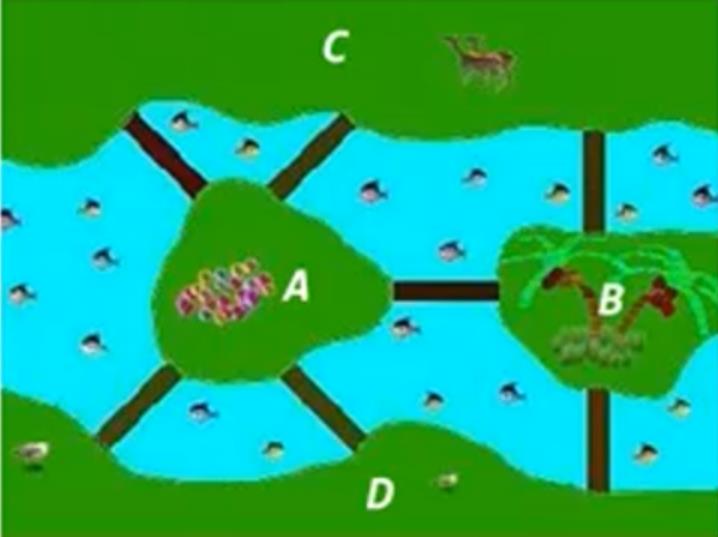
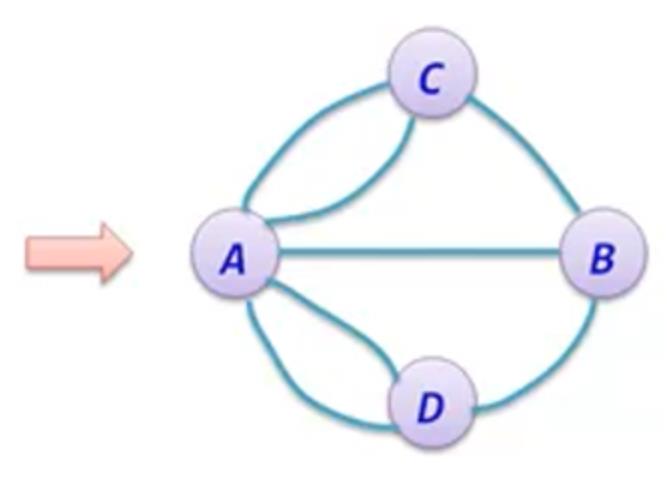
ADT Graph

图抽象数据类型=逻辑结构+基本运算(运算描述)
图的基本运算如下:

1. CreateGraph(&g):创建图
2. DestroyGraph(&g):销毁图
3. DispGraph(g):输出图
4. DFS(g, v):从顶点v出发深度优先遍历
5. BFS(g, v) 从顶点v出发广度优先遍历。

有向图与无向图

有向图

在图G中，如果代表边的顶点对是无序的，则称G为无向图
用圆括号序偶表示无向边

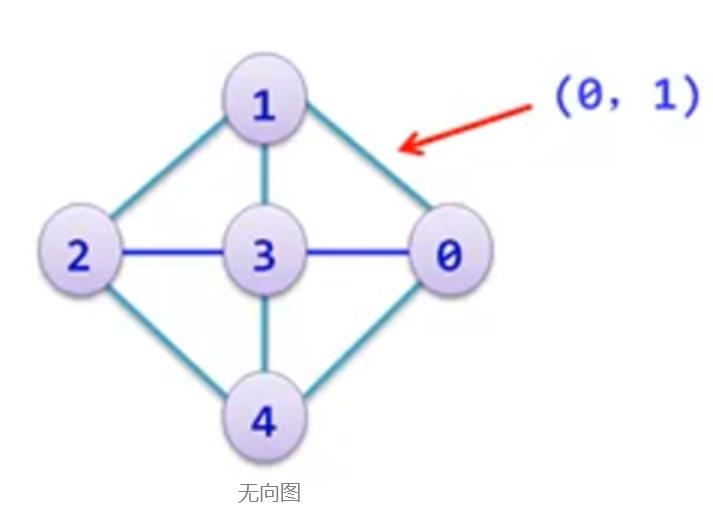
无向图

如果表示边的顶点对是有序的，则称G为有向图
用尖括号序偶表示有向边

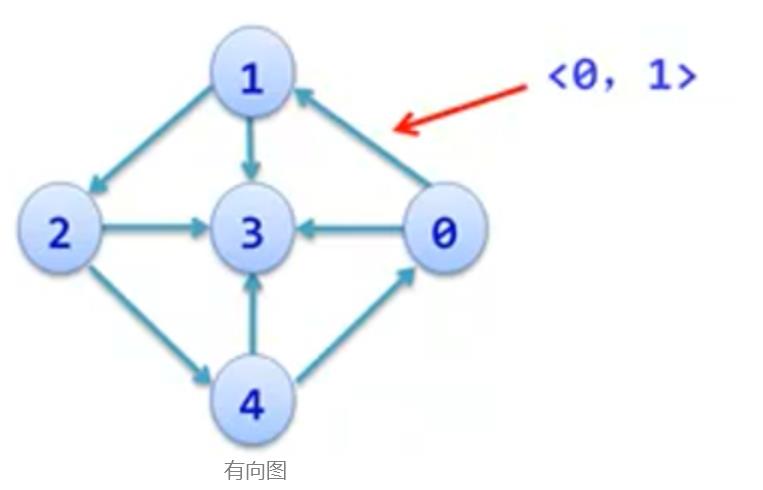
图的基本术语

端点和邻接点

在一个无向图中,若 存在一条边(i,j), 则称顶点i和顶点j为该边的两个端点(endpoint),并称它们互为邻接点(adjacent),即顶点i是顶点j的一个邻接点,顶点j也是顶点i的一个邻接点,边(i,j)和顶点 ij关联。

关联于相同两个端点的两条或者两条以上的边称为多重边,在数据结构中讨论的图都是指没有多重边的图

在一个有向图中,若存在一条有向边<i,j>(也称为弧),则称此边是顶点 i的一条出边,同时也是顶点j的一条入边,i为此边的起始端点(简称为起点),j为此边的终止端点(简称终点), 顶点j是顶点i的出边邻接点，顶点 i 是顶点j的入边邻接点

顶点的度、入度和出度

无向图中：

一个顶点所关联的边的数目称为该顶点的度(degree)

有向图中：

顶点的度又分为入度和出度
以顶点j为终点的边数目,称为该顶点的入度(indegree)
以顶点 i为起点的边数目,称为该顶点的出度（outdegree)
一个顶点的入度与出度的和为该顶点的度
一个图中所有顶点的度之和等于边数的两倍
因为图中的每条边分别作为两个邻接点的度各计一次

完全图

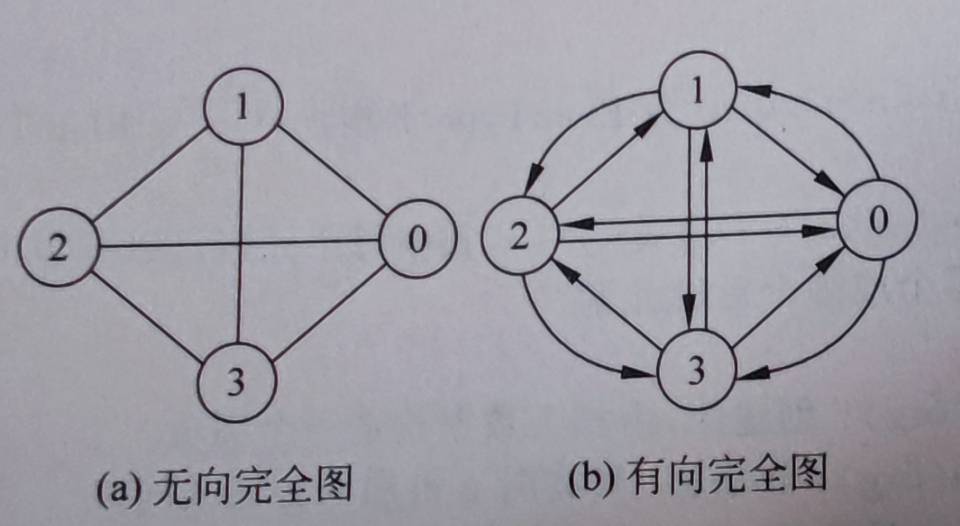
无向完全图：无向图中，任意两个顶点之间都存在边
有向完全图：有向图中，任意两个顶点之间都存在方向互为相反的两条弧

稠密图和稀疏图

稀疏图：一个图有很少条边时
稠密图：当一个图接近完全图，有很多条边时

子图

子图：
若有两个图：G=(V,E),G’=(V’,E’)
若V’是V的（真）子集，E’是E的（真）子集
且E’中的边仅与V’中的顶点相关联
则G’是G的（真）子图

路径和路径长度

路径：
图G中，从任一顶点开始，由边或弧的邻接关系构成的有限长顶点序列称为路径

简单路径：
序列中顶点不重复出现的路径

回路：
序列中第一个顶点和最后一个顶点相同的路径

简单回路：
序列中第一个顶点和最后一个顶点相同的简单路径

注意：
有向图的路径必须沿弧的方向构成顶点序列；
构成路径的顶点可能重复出现 (即允许反复绕圈)

连通、连通图、连通分量、可达

连通：
无向图G中，若从顶点i到顶点j有路径，则称顶点i与顶点j是连通的
连通图：
图中任意两个顶点都是连通的
极大连通子图：
该子图是G连通子图，将G的任何不在该子图的顶点加入，子图将不再连通
极小连通子图：
该子图是G的连通子图，在该子图中删除任何一条边，子图都将不再连通
连通分量：
无向图G中的极大连通子图称为G的连通分量
可达：
有向图中顶点v到w有路径称v到w是可达的

强连通图和强连通分量

强连通图：
有向图中任意两个不同顶点都是可达的称之为强连通图
连通分量：
无向图的极大连通子图称为连通分量
有向图的极大强连通子图称为强连通分量或连通分量

权和网

权（Weight）：
与图的边或弧相关的数
网（Network）：
带权的图

图的存储结构

邻接矩阵存储方法

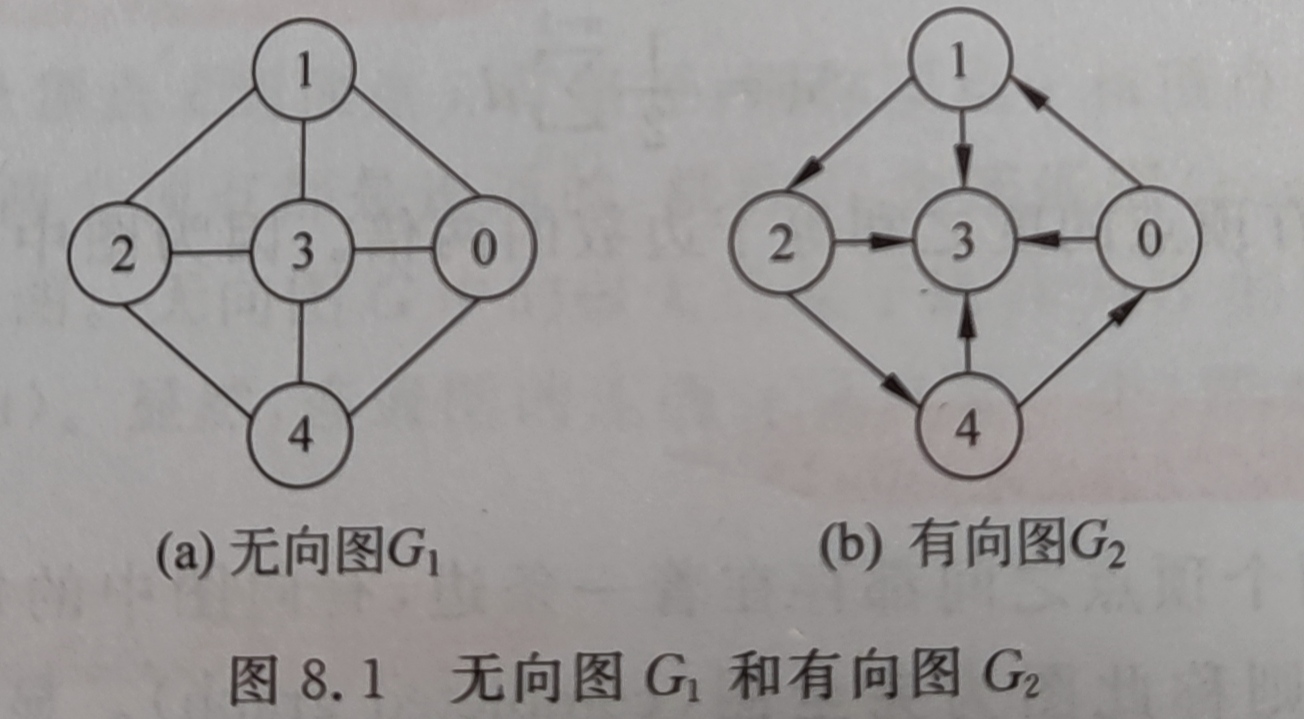
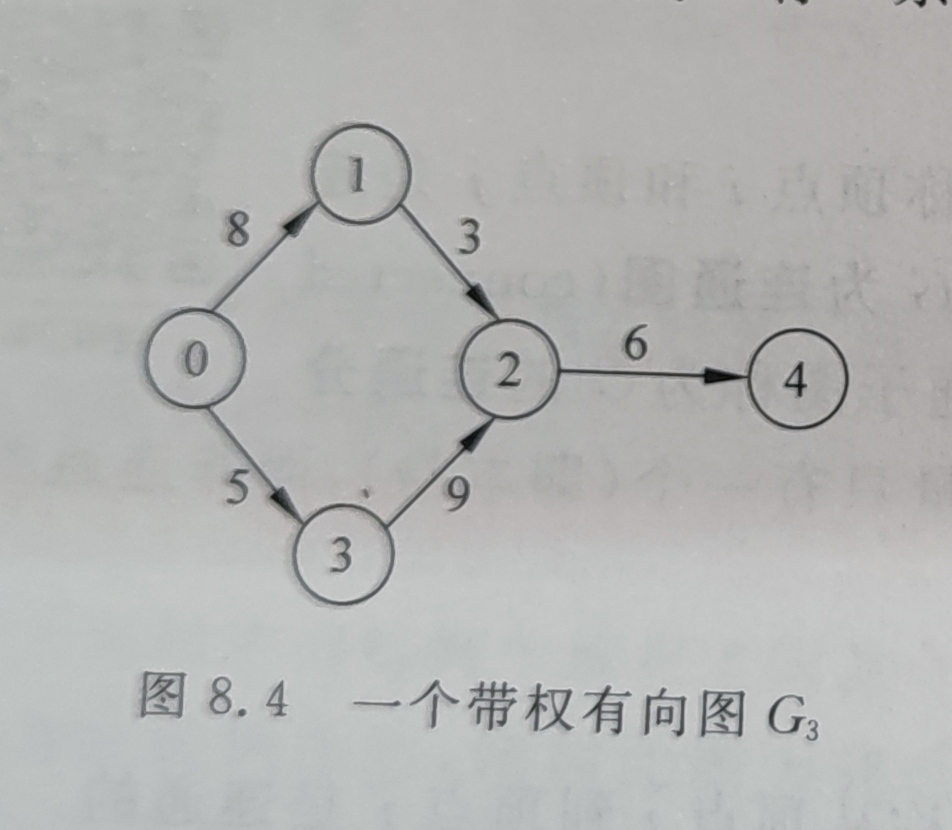
代码实现

#define MAXV<最大顶点个数>
#define INF 32767  ///定义∞
typedef struct

    int no;             ///顶点的编号
    InfoType info       ///顶点的其他信息
VertexType;            ///顶点的类型

typedef struct

    int edgs[MAXV][MAXV];   ///邻接矩阵数组 
    int n,e;                ///顶点数、边数
    VertexType vexs[MAXV]; ///顶点的类型
MatGraph;      ///完整的图邻接矩阵类型