自动驾驶控制概况

Posted 2023-03-12 yuan〇

文章目录

• 1. 第一章行为决策在自动驾驶系统架构中的位置
• 2. 路径跟踪控制的种类
• • 2.1 基于自行车模型的路径跟踪控制算法
  • • 2.1.1 纯跟踪控制（Pure Pursuit）算法
    • 2.1.2 后轮反馈控制算法（Rear wheel feedback）
    • 2.1.3前轮反馈控制算法（Front wheel position based feedback）
  • 2.2 基于运动学模型的轨迹跟踪控制
  • • 2.2.1 基于Lyapunov函数的控制
    • 2.2.2 输出反馈线性化控制
  • 2.3 MPC控制
  • 2.4 PID控制
  • 2.5 LQR控制
  • 2.6 滑模控制
• 参考文献

1. 第一章行为决策在自动驾驶系统架构中的位置

    Claudine Badue^[1]等人以圣西班牙联邦大学（UFES）开发的自动驾驶汽车（Intelligent Autonomous Robotics Automobile，IARA）为例，提出了自动驾驶汽车的自动驾驶系统的典型架构。如图所示，自动驾驶系统主要由感知系统（Perception System）和规划决策系统（Decision Making System）组成。感知系统主要由交通信号检测模块（Traffic Signalization Detector，TSD）、移动目标跟踪模块（Moving Objects Tracker，MOT）、定位与建图模块（Localizer and Mapper）等组成。规划决策系统主要由全局路径规划模块（Route Planner）、局部路径规划模块（Path Planner）、行为决策模块（Behavior Selector）、运动规划模块（Motion Planner）、自主避障模块(Obstacle Avoider)以及控制模块（Controller）组成。

图1-1 自动驾驶系统架构图

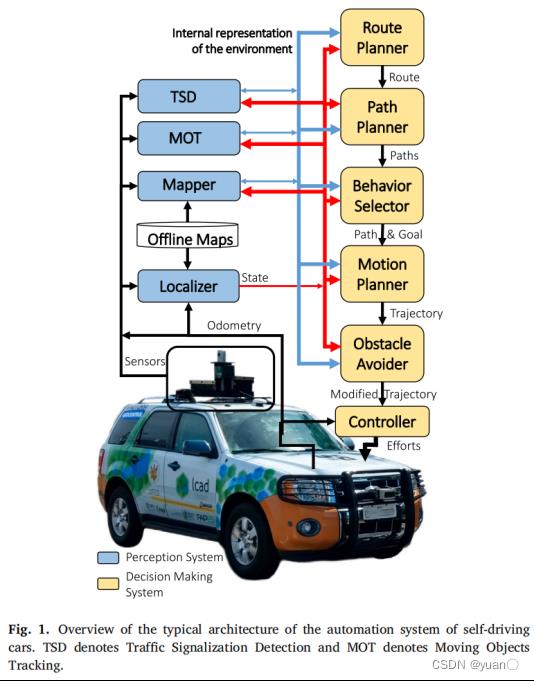
    路径跟踪控制在此架构中主要是由控制模块实现。控制模块接收最终由自主避障模块修改的运动计划轨迹，计算并发送相应的控制指令给方向盘、油门和制动器的执行器，以使汽车在现实世界规则允许的情况下执行修改后的轨迹。

2. 路径跟踪控制的种类

    自动驾驶汽车路径跟踪控制算法，主要是控制车辆按照上层路径规划器规划好的路径进行无偏差横纵向控制。目前自动驾驶汽车横向控制算法主要分为两种，包括有模型和无模型的控制方法[2]。无模型横向控制方法即传统的比例-积分-微分控制（Proportional Integral Derivative，PID），另一种是基于模型的横向控制方法，其中根据控制模型的不同，控制器又可分为有基于运动学模型的控制器和基于动力学模型的控制器。

    车辆运动学模型通常将车辆简化为一个质点,即为质点模型；或将车辆的垂直方向移动忽略、将车辆的同车轴的车轮角速度相同、将车辆的朝向简化为前轮的朝向，即简化为自行车模型，基于该模型的控制方法主要有纯跟踪控制（Pure Pursuit）算法、Stanley 控制算法，后轮反馈控制算法（Rear wheel feedback）。该类型控制器通常是通过控制航向角和横向误差来计算转向角，易于实现，但该模型仅适用于不考虑车辆动力学的低速行驶工况，如自动泊车控制系统。如果考虑复杂城市工况和高速交通环境时，则基于运动学模型的控制器的可靠性和鲁棒性并不高，因此就需要引入车辆动力学模型。

     基于车辆动力学模型的控制算法主要有线性二次型调节器（Linear Quadratic Regulator，LQR）、模型预测控制（Model Predictive Control，MPC）、滑模控制（Sliding Model Control，SMC）等，由于其考虑了车辆高速行驶时车身与外界干扰项等多重因素，如轮胎的非线性变化、车辆横摆与侧倾约束、路面曲率变化等，进一步提高了车辆行驶于复杂工况的安全性和可 靠性。目前的车辆动力学模型通常是简化了的二自由度单车模型，其保留了车辆的横摆和侧向运动，在能够准确描述车辆动力学的基础上尽量简化了车辆模型，以减少算法的计算量，确保控制系统的实时性。

2.1 基于自行车模型的路径跟踪控制算法

2.1.1 纯跟踪控制（Pure Pursuit）算法

     纯追踪控制是最早提出的路径跟踪策略之一。由于其易于实现和令人满意的性能，已被证明是车辆控制不可或缺的工具。在DARPA挑战赛中，有多个团队采用了纯追踪的控制算法^[3]。

     从自行车模型出发，纯跟踪算法以车后轴为切点, 车辆纵向车身为切线, 通过控制前轮转角,使车辆可以沿着一条经过目标路点（goal point）的圆弧行驶，如图2-1所示。

     通过正弦定理求出曲率、偏转角与车轴之间的关系：$$k=\frac{2\sin \alpha }{l_d}$$式中 $l_d$——车辆当前位置到目标路点的距离；
     $A$——目前车身姿态和目标路点的夹角。

图2-1 纯追踪控制示意图

    前轮的转向角 $\delta$ 的表达式为：$$\delta =\arctan (kL)$$    纯追踪算法控制量的的最终表达式：$$\delta (t)=\arctan (\frac{2L\sin (\alpha (t)}{l_d})$$    为了更好的理解纯追踪控制器的原理，我们定义一个新的量：$e_l$—— 车辆当前姿态和目标路点在横向上的误差，由此可得夹角正弦：$$\sin (\alpha )=\frac{e_l}{l_d}$$    圆弧的弧度就可重写为：$$k=\frac{2}{l_d^2}{e}_l$$    考虑到本质是横向上的跟踪偏差(Cross Track Error, CTE)，由上式可知纯追踪控制器其实是一个横向转角的$P$控制器，其$P$系数为 $2/(l_d{)}^2$；这个P控制器受到参数 $l_d$（即前视距离）的影响很大，如何调整前视距离变成纯追踪算法的关键；通常来说，$l_d$ 被认为是车速的函数，在不同的车速下需要选择不同的前视距离。一种最常见的调整前视距离的方法就是将前视距离表示成车辆纵向速度的线形函数，即$l_d=k{v}_x$，那么前轮的转角公式就变成了：$$\delta (t)=\arctan (\frac{2L\sin (\alpha (t))}{k{v}_x(t)})$$    通常来说，会使用最大、最小前视距离来约束前视距离，越大的前视距离意味着轨迹的追踪越平滑，小的前视距离会使得追踪更加精确（当然也会带来控制的震荡），如图2-2 所示。

    驾驶员在实际驾驶过程中会观察车辆前方一定距离范围内的道路信息，以获得一定的预见性,提前对车辆进行调整，从而取得良好的控制效果。在路径跟踪过程中，前视距离与车速的大小有直接的关系。当车速较高时，需要较大的前视距离；当车速较低时,较小的前视距离可以达到很好的跟踪精度。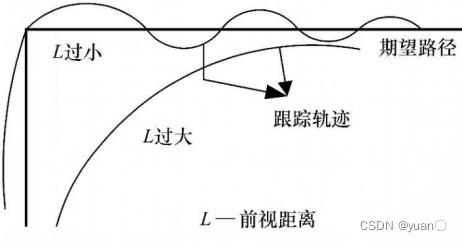

图2-2 前视距离对控制的影响

2.1.2 后轮反馈控制算法（Rear wheel feedback）

    后轮反馈控制是利用后轮中心的跟踪偏差来进行转向控制量计算的方法，最早由Claude Samson^[4]提出。如图2-3所示，先找到车辆后轮距离参考轨迹上最近的点。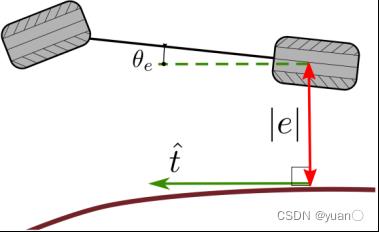

图2-3 后轮反馈控制示意图

    该点满足的轨迹曲线方程为：$$s(t)=\arg \min \Vert (x_r(t),y_r(t))-(x_{ref}(\gamma ),y_{ref}(\gamma ))\Vert$$    对该曲线进行求导，得：$$\hat{t}=\frac{\left({\frac{\partial x_{ref}}{\partial s}|}_{s(t)},{\frac{\partial y_{ref}}{\partial s}|}_{s(t)}\right)}{\Vert \left(\frac{\partial x_{ref}\left(s(t)\right)}{\partial s},\frac{\partial y_{ref}\left(s(t)\right)}{\partial s}\right)\Vert }$$    车辆和切线之间的角度差为： θ t = θ − arctan ⁡ 2 ( ∂ y r e f ( s ( t ) ) ∂ s , ∂ x r e f ( s ( t ) ) ∂ s