堆的定义及其基本操作（存储建立插入删除）

Posted 2021-12-23 薛定谔的猫ovo

文章目录

• • 堆的定义
  • 堆的存储
  • 堆的建立
  • • 建立小根堆
    • 建立大根堆
  • 堆的插入
  • • 小根堆的插入
    • 大根堆的插入
  • 堆的删除
  • • 小根堆的删除
    • 大根堆的删除
  • 完整代码
  • 说明

---

堆的定义

堆的定义如下：
$n$个关键字序列$L[1...n]$称为堆，当且仅当该序列满足：
$L[i]\le L[2i]$ 且 $L[i]\le L[2i+1]$ （小根堆）
或者 $L[i]\ge L[2i]$ 且 $L[i]\ge L[2i]$ （大根堆） （$1\le i\le \lfloor n/2\rfloor$）
则称这个序列为小根堆（或大根堆）

---

堆的存储

堆在逻辑上是一个完全二叉树组织的非线性结构，在物理上是用一个一维数组存储的。

堆的类型定义如下：

#define maxSize 20
typedef struct
    int heap[maxSize];  //存放堆中元素的数组，一般从下标1开始存储(为了对应完全二叉树)
    int n; //当前元素个数
Heap;

---

堆的建立

建立小根堆

建立小根堆的基本思路是：
 堆记录数组从编号最大的非叶结点开始，$i=\lfloor n/2\rfloor$，…，$2$，$1$，使用筛选算法将结点 $i$ 为根的子树调整成堆，从局部到整体，逐步扩大小根堆，最后完成小根堆的创建。

实现的核心代码：

//小根堆的向下调整算法
void AdjustDown(Heap &H, int k, int len)
    //将元素k向下调整
    H.heap[0] = H.heap[k]; //暂存H.heap[k]的值
    for(int i=2*k; i<=len; i*=2) //延关键字较小的子结点向下筛选
        if(i<len && H.heap[i]>H.heap[i+1])
            i++; //选取关键字较小的子结点的下标
        if(H.heap[0] <= H.heap[i])
            break;  //筛选结束
        else
            H.heap[k] = H.heap[i];  //将H.heap[i]调整到双亲结点上
            k = i; //修改k值，以便继续向下筛选
        
    
    H.heap[k] = H.heap[0];  //被筛选结点的值放入最终位置


//建立小根堆
void CreateMinHeap(Heap &H, int arr[], int len)
    for(int i=0; i<len; i++)
        H.heap[i+1] = arr[i]; //从下标1开始存储
    
    H.n = len+1; //长度需加1
    for(int i=len/2; i>0; i--)
        AdjustDown(H,i,len);  //从i=n/2 ~ 1，反复调整堆
    

为了保证文章的可读性，完整代码在文章最后。

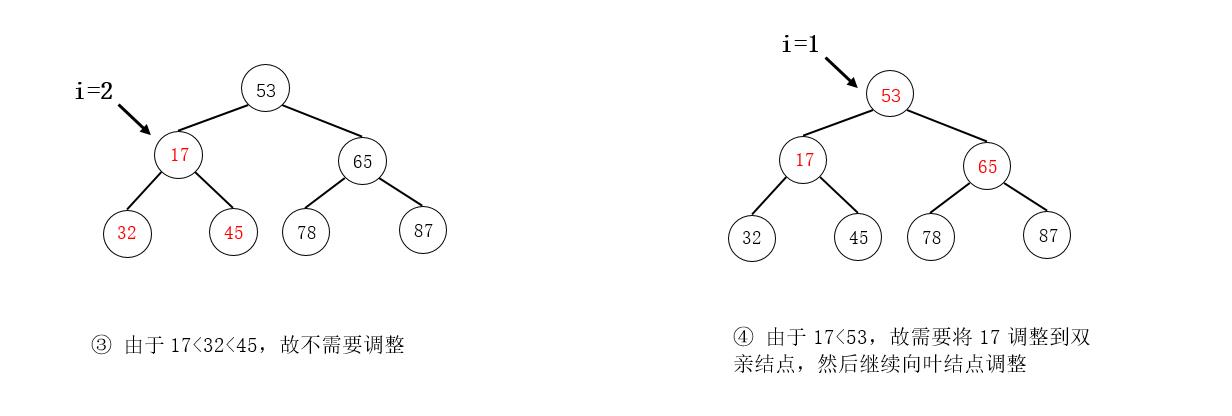
例如，将如下图所示的待排序列形成的完全二叉树调整为小根堆：

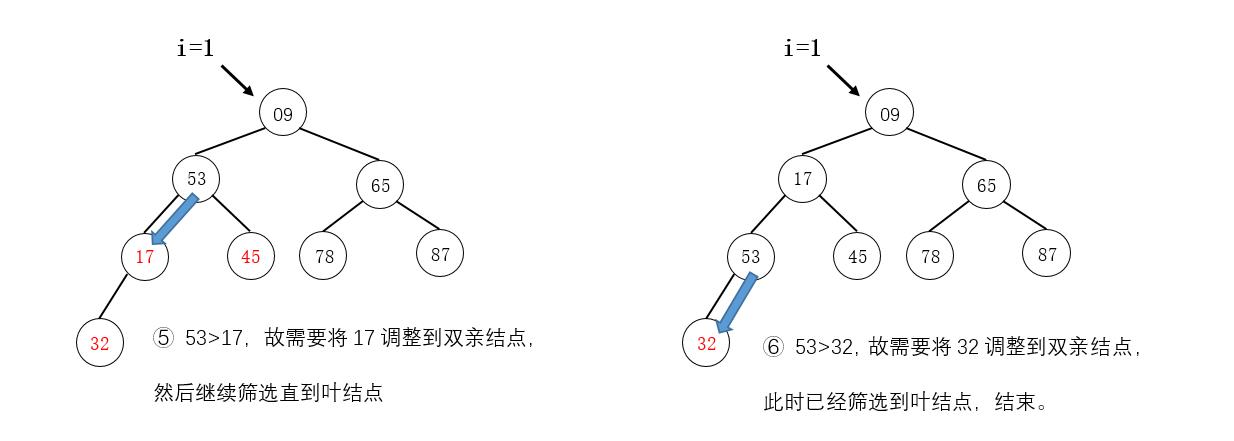
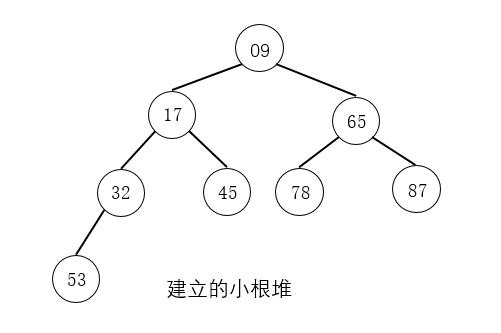
注意

在图示中，我们是找到需要调整的结点直接交换其结点值，而在算法的实现上，是暂存要调整的结点值，在最后找到被筛选结点的最终位置时，直接放入最终位置。

---

建立大根堆

建立大根堆与建立小根堆的基本思路相同，不过是要寻找关键字较大的结点向上调整。

建立大根堆的基本思路是：
 堆记录数组从编号最大的非叶结点开始，$i=\lfloor n/2\rfloor$，…，$2$，$1$，使用筛选算法将结点 $i$ 为根的子树调整成堆，从局部到整体，逐步扩大大根堆，最后完成大根堆的创建。

实现的核心代码：

//大根堆的向下调整算法
void AdjustDown2(Heap &H, int k, int len)
    //将元素k向下调整
    H.heap[0] = H.heap[k]; //暂存H.heap[k]的值
    for(int i=2*k; i<=len; i*=2) //延关键字较大的子结点向下筛选
        if(i<len && H.heap[i]<H.heap[i+1])
            i++; //选取关键字较大的子结点的下标
        if(H.heap[0] >= H.heap[i])
            break;  //筛选结束
        else
            H.heap[k] = H.heap[i];  //将H.heap[i]调整到双亲结点上
            k = i; //修改k值，以便继续向下筛选
        
    
    H.heap[k] = H.heap[0];  //被筛选结点的值放入最终位置


//建立大根堆
void CreateMaxHeap(Heap &H, int arr[], int len)
    for(int i=0; i<len; i++)
        H.heap[i+1] = arr[i]; //从下标1开始存储
    
    H.n = len+1; //长度需加1
    for(int i=len/2; i>0; i--)
        AdjustDown2(H,i,len);  //从i=n/2 ~ 1，反复调整堆
    

为了保证文章的可读性，完整代码在文章最后。

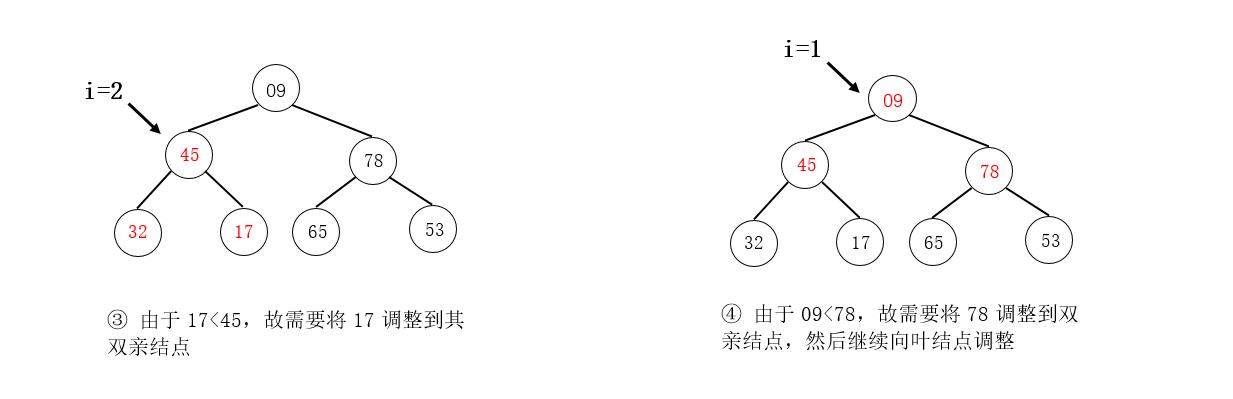
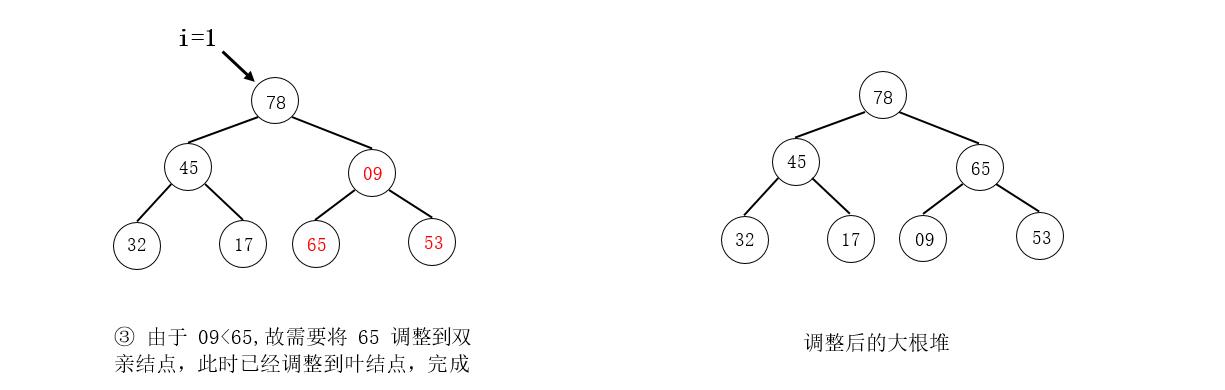
例如，将如下图所示的待排序列形成的完全二叉树调整为大根堆：

注意

在图示中，我们是找到需要调整的结点直接交换其结点值，而在算法的实现上，是暂存要调整的结点值，在最后找到被筛选结点的最终位置时，直接放入最终位置。

---

堆的插入

小根堆的插入

小根堆的插入算法调用了另一种堆的排序算法$AdjustUp$，实现自下而上的筛选。

每次新结点插入在已经建成的小根堆的后面，即$H.data[n+1]$的位置，此时小根堆被破坏，不满足小根堆的性质，于是需要用$AdjustUp$算法向下调整使其继续保持小根堆的性质。
具体实现为从新结点插入位置开始，向上与双亲的关键码进行比较，若小于双亲的关键码，则双亲所存的数据下移，再继续向上比较处理；若大于等于双亲的关键码，则停止向上比较，回送新插入元素，重新调整为小根堆。

实现代码：

//小根堆向上调整算法
void AdjustUp1(Heap &H, int k)
    //参数k为向上调整的点，也是堆的元素个数
    H.heap[0] = H.heap[k]; //暂存H.heap[k]的值
    int i=k/2; //若结点值小于双亲结点，则将双亲结点向下调，并继续向上比较
    while(i>0 && H.heap[i]>H.heap[0])  //循环跳出条件
        H.heap[k] = H.heap[i];  //双亲结点下调
        k = i;
        i = k/2;  //继续向上比较
    
    H.heap[k] = H.heap[0];  //复制到最终位置


//小根堆的插入算法
void InsertMin(Heap &H, int x)
    if(H.n == maxSize)
        cout<<"堆满，无法插入!"<<endl; //堆满，无法插入
    H.heap[H.n] = x; //新值插入到最后
    AdjustUp1(H, H.n);  //从下向上调整
    H.n++; //堆计数加一

例如，在下图所示的小根堆中插入元素06：

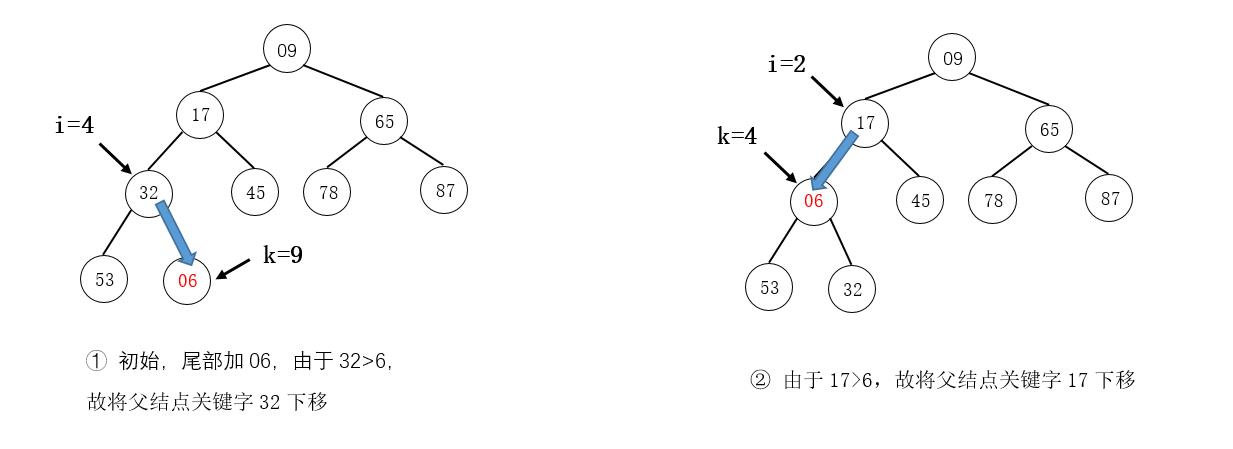
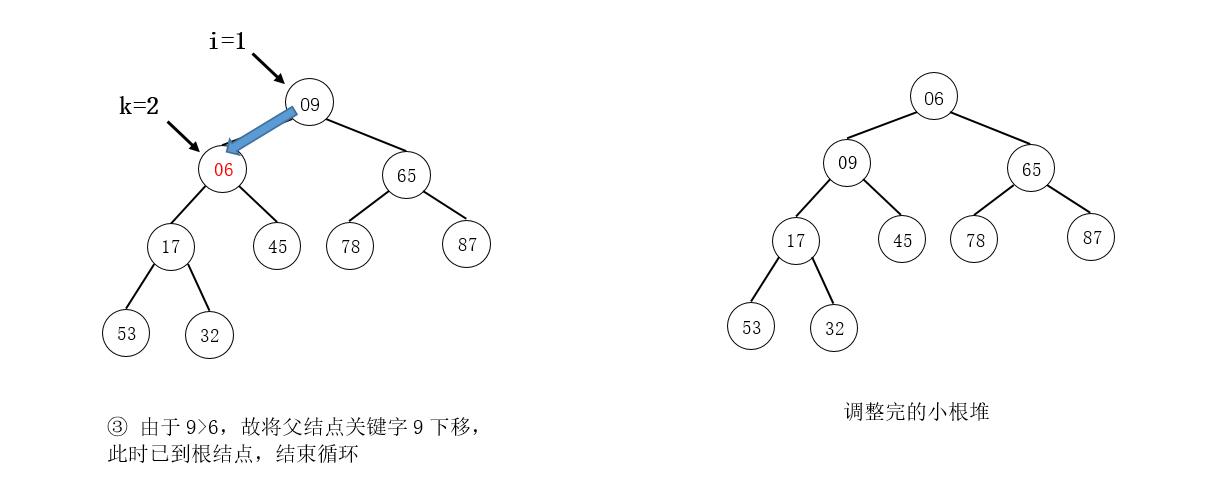
注意

同样，在图示中，我们是找到需要调整的结点直接交换其结点值，而在算法的实现上，是暂存要调整的结点值，在最后找到被筛选结点的最终位置时，直接放入最终位置。

---

大根堆的插入

大根堆的插入算法也是调用了另一种堆的排序算法$AdjustUp$，实现自下而上的筛选。

每次新结点插入在已经建成的大根堆的后面，即$H.data[n+1]$的位置，此时大根堆被破坏，不满足大根堆的性质，于是需要用$AdjustUp$算法向下调整使其继续保持大根堆的性质。
具体实现为从新结点插入位置开始，向上与双亲的关键码进行比较，若大于双亲的关键码，则双亲所存的数据下移，再继续向上比较处理；若小于等于双亲的关键码，则停止向上比较，回送新插入元素，重新调整为大根堆。

实现代码：

//大根堆向上调整算法
void AdjustUp2(Heap &H, int k)
    //参数k为向上调整的点，也是堆的元素个数
    H.heap[0] = H.heap[k]; //暂存H.heap[k]的值
    int i=k/2; //若结点值大于双亲结点，则将双亲结点向下调，并继续向上比较
    while(i>0 && H.heap[i]<H.heap[0])  //循环跳出条件
        H.heap[k] = H.heap[i];  //双亲结点下调
        k = i;
        i = k/2;  //继续向上比较
    
    H.heap[k] = H.heap[0];  //复制到最终位置


//大根堆的插入算法
void InsertMax(Heap &H, int x)
    if(H.n == maxSize)
        cout<<"堆满，无法插入!"<<endl; //堆满，无法插入
    H.heap[H.n] = x; //新值插入到最后
    AdjustUp2(H, H.n);  //从下向上调整
    H.n++; //堆计数加一

例如，在下图所示的大根堆中插入元素63：

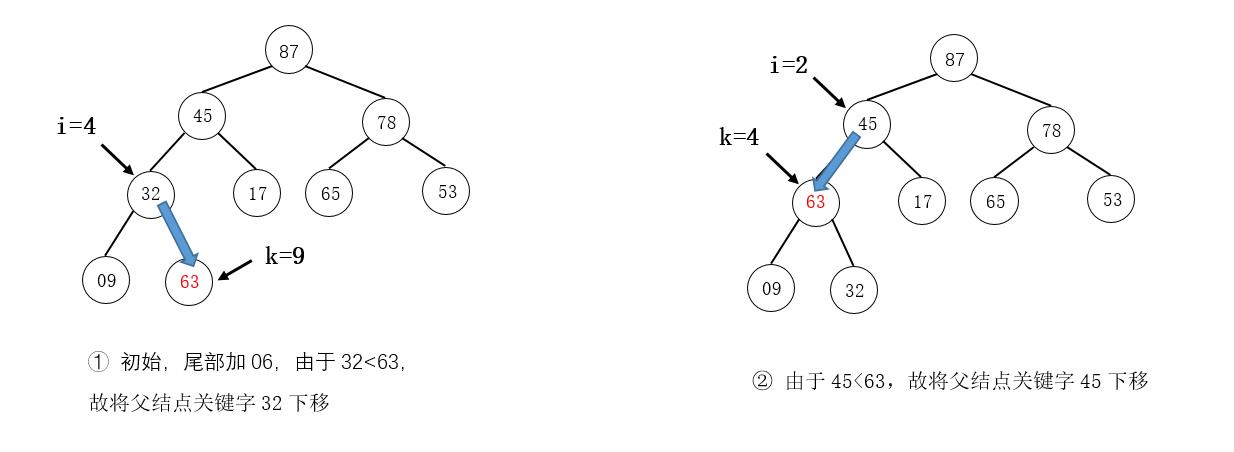
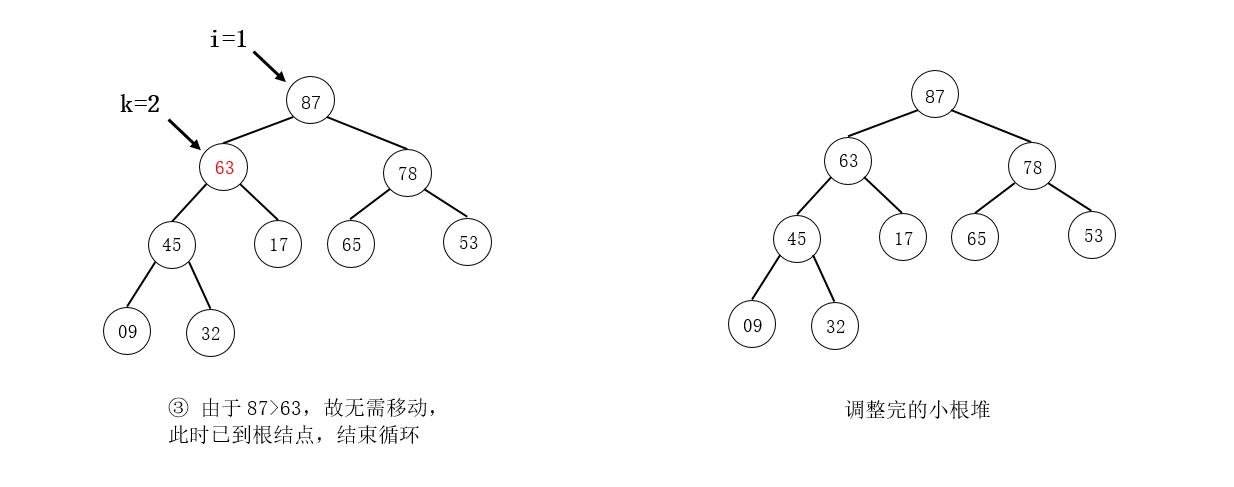
注意

同样，在图示中，我们是找到需要调整的结点直接交换其结点值，而在算法的实现上，是暂存要调整的结点值，在最后找到被筛选结点的最终位置时，直接放入最终位置。

---

堆的删除

小根堆的删除

每次删除元素总是小根堆的堆顶（对应完全二叉树的根）元素，它是具有最小关键码的记录。在把这个元素取走后，以堆的最后一个元素填补取走的堆顶元素，并将堆的实际元素个数减1。最后用$AdjustDown$算法从堆顶向下进行调整，使其继续保持小根堆的性质。

实现代码：

//小根堆的删除算法
void RemoveMin(Heap &H, int &x)
    if(H.n == 1) //只剩下H.heap[0]
        cout<<"堆为空。"<<endl;
    x = H.heap[1];  //取出堆顶元素
    H.heap[1] = H.heap[H.n-1];  //最后一个元素填补
    H.n--;  //元素个数减1
    AdjustDown1(H, 1, H.n-1);  //自上向下调整堆

例如，在下图所示的小根堆中删除元素09：

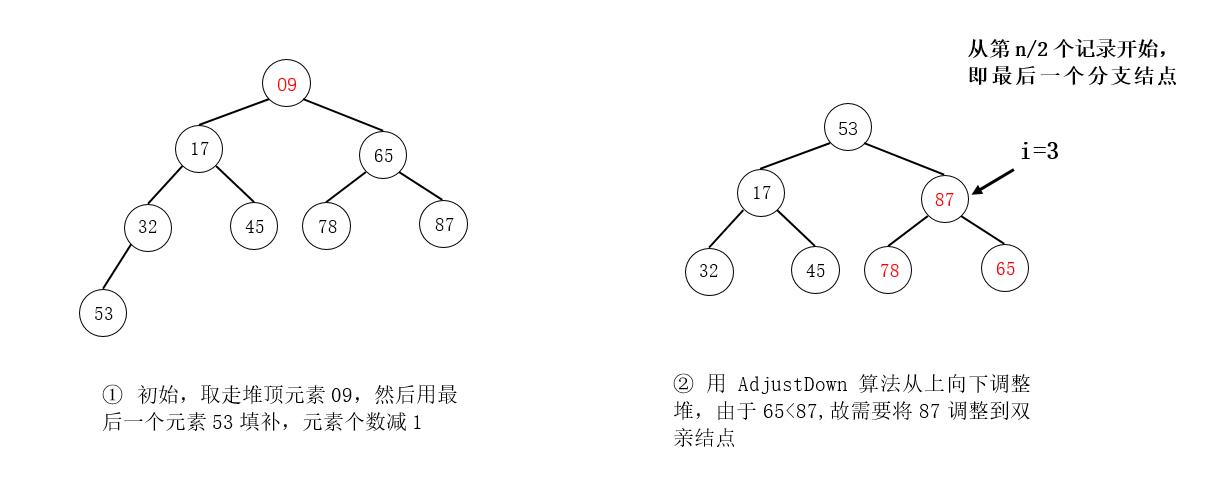
注意

同样，在图示中，我们是找到需要调整的结点直接交换其结点值，而在算法的实现上，是暂存要调整的结点值，在最后找到被筛选结点的最终位置时，直接放入最终位置。

---

大根堆的删除

每次删除元素总是大根堆的堆顶（对应完全二叉树的根）元素，它是具有最大关键码的记录。在把这个元素取走后，以堆的最后一个元素填补取走的堆顶元素，并将堆的实际元素个数减1。最后用$AdjustDown$算法从堆顶向下进行调整，使其继续保持大根堆的性质。

实现代码：

//大根堆的删除算法
void RemoveMax(Heap &H, int &x)
    if(H.n == 1) //只剩下H.heap[0]
        cout<<"堆为空。"<<endl;
    x = H.heap[1];  //取出堆顶元素
    H.heap[1] = H.heap[H.n-1];  //最后一个元素填补
    H.n--;  //元素个数减1
    AdjustDown2(H, 1, H.n-1);  //自上向下调整堆

例如，在下图所示的大根堆中删除元素87：

注意

同样，在图示中，我们是找到需要调整的结点直接交换其结点值，而在算法的实现上，是暂存要调整的结点值，在最后找到被筛选结点的最终位置时，直接放入最终位置。

---

完整代码

#include<bits/stdc++.h>
using namespace std;

#define maxSize 20
typedef struct
    int heap[maxSize];  //存放堆中元素的数组，一般从下标1开始存储(为了对应完全二叉树)
    int n; //当前元素个数
Heap;

//输出
void PrintHeap(Heap H)
    for(int i=1; i<H.n; i++) //从1开始输出
        cout<<H.heap[i]<<" ";
    
    cout<<endl<<endl;


//小根堆的向下调整算法
void AdjustDown1(Heap &H, int k, int len)
    //将元素k向下调整
    H.heap[0] = H.heap最小堆的建立 插入 与删除

 堆的插入和删除
 堆的插入和删除
 最小堆（优先队列）基本概念，即一个完整建立，插入，删除代码
 （透彻理解）最精锐代码::堆的三种基本操作新建-插入-删除
 数据结构之堆