单目标优化求解基于matlab秃鹰算法（BES）求解最优目标问题含Matlab源码 1546期

Posted 2021-12-22 紫极神光

一、秃鹰算法（BES）简介

1 秃鹰搜索优化算法
秃鹰遍布于北美洲地区, 飞行中视力敏锐, 观察能力优秀. 以捕食鲑鱼为例, 秃鹰首先会基于个体和种群到鲑鱼的浓度来选择搜索空间, 朝一个特定区域飞行; 其次在选定搜索空间内搜索水面, 直到发现合适的猎物; 最后秃鹰会逐渐改变飞行高度, 快速向下俯冲, 从水中成功捕获鲑鱼等猎物.BES 算法以秃鹰捕食猎物的行为进行模拟, 将其分为选择搜索空间、搜索空间猎物和俯冲捕获猎物三个阶段, 数学模型如下所示:

1. 选择搜索空间: 秃鹰随机选择搜索区域, 通过判断猎物数目来确定最佳搜寻位置, 便于搜索猎物,该阶段秃鹰位置 Pi,new 更新由随机搜索的先验信息乘以 α 来确定. 该行为数学模型描述为:
   
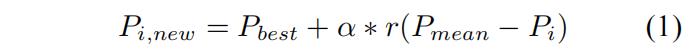
   式中:α 表示控制位置变化参数, 变化范围为 (1.5,2);r 为 (0,1) 间随机数;Pbest 为当前秃鹰搜索确定的最佳搜索位置;Pmean 为先前搜索结束后秃鹰的平均分布位置;Pi 为第 i 只秃鹰位置.
2. 搜索空间猎物 (探索): 秃鹰在选定搜索空间内以螺旋形状飞行搜索猎物, 加速搜索进程, 寻找最佳俯冲捕获位置. 螺旋飞行数学模型采用极坐标方程进行位置更新, 如下所示:
   
3. 俯冲捕获猎物 (利用): 秃鹰从搜索空间的最佳位置快速俯冲飞向目标猎物, 种群其他个体也同时向最佳位置移动并攻击猎物, 运动状态仍用极坐标方程描述, 如下:
   
   2 莱维飞行策略
   莱维飞行源于 Levy 的对称莱维稳定分布积分,是一种生成特殊的随机步长方法, 飞行步长服从重尾的指数概率分布 (Levy 分布). 其服从参数 (步长) 为 s 的分布公式为:
   

二、部分源代码

clc;
clear;
number_fun='F2';
MaxIt=1000;
nPop=80;
[low,high,dim,fun] = Get_Functions_details(number_fun);
[value,fun_hist]=BES(nPop,MaxIt,low,high,dim,fun);
% plot(fun_hist,'-','Linewidth',1.5)
% xlabel('Iteration')
% ylabel('fitness')
% legend('BES')
figure('Position',[500 500 660 290])

subplot(1,2,1);
func_plot(number_fun);
title('Objective space')
xlabel('x_1');
ylabel('x_2');
zlabel([number_fun,'( x_1 , x_2 )'])

subplot(1,2,2);
plots=semilogx(fun_hist,'Color','r');
set(plots,'linewidth',2)
hold on
title('Objective space')
xlabel('Iterations');
ylabel('Best score');
function [lowerbound,upperbound,dimension,fitness] = fun_info(F)


switch F
    case 'F1'
        fitness = @F1;
        lowerbound=-100;
        upperbound=100;
        dimension=30;
        
    case 'F2'
        fitness = @F2;
        lowerbound=-10;
        upperbound=10;
        dimension=30;
        
    case 'F3'
        fitness = @F3;
        lowerbound=-100;
        upperbound=100;
        dimension=30;
        
    case 'F4'
        fitness = @F4;
        lowerbound=-100;
        upperbound=100;
        dimension=30;
        
    case 'F5'
        fitness = @F5;
        lowerbound=-30;
        upperbound=30;
        dimension=30;
        
    case 'F6'
        fitness = @F6;
        lowerbound=-100;
        upperbound=100;
        dimension=30;
        
    case 'F7'
        fitness = @F7;
        lowerbound=-1.28;
        upperbound=1.28;
        dimension=30;
        
    case 'F8'
        fitness = @F8;
        lowerbound=-500;
        upperbound=500;
        dimension=30;
        
    case 'F9'
        fitness = @F9;
        lowerbound=-5.12;
        upperbound=5.12;
        dimension=30;
        
    case 'F10'
        fitness = @F10;
        lowerbound=-32;
        upperbound=32;
        dimension=30;
        
    case 'F11'
        fitness = @F11;
        lowerbound=-600;
        upperbound=600;
        dimension=30;
        
    case 'F12'
        fitness = @F12;
        lowerbound=-50;
        upperbound=50;
        dimension=30;
        
    case 'F13'
        fitness = @F13;
        lowerbound=-50;
        upperbound=50;
        dimension=30;
        
    case 'F14'
        fitness = @F14;
        lowerbound=-65.536;
        upperbound=65.536;
        dimension=2;
        
    case 'F15'
        fitness = @F15;
        lowerbound=-5;
        upperbound=5;
        dimension=4;
        
    case 'F16'
        fitness = @F16;
        lowerbound=-5;
        upperbound=5;
        dimension=2;
        
    case 'F17'
        fitness = @F17;
        lowerbound=[-5,0];
        upperbound=[10,15];
        dimension=2;
        
    case 'F18'
        fitness = @F18;
        lowerbound=-2;
        upperbound=2;
        dimension=2;
        
    case 'F19'
        fitness = @F19;
        lowerbound=0;
        upperbound=1;
        dimension=3;

三、运行结果

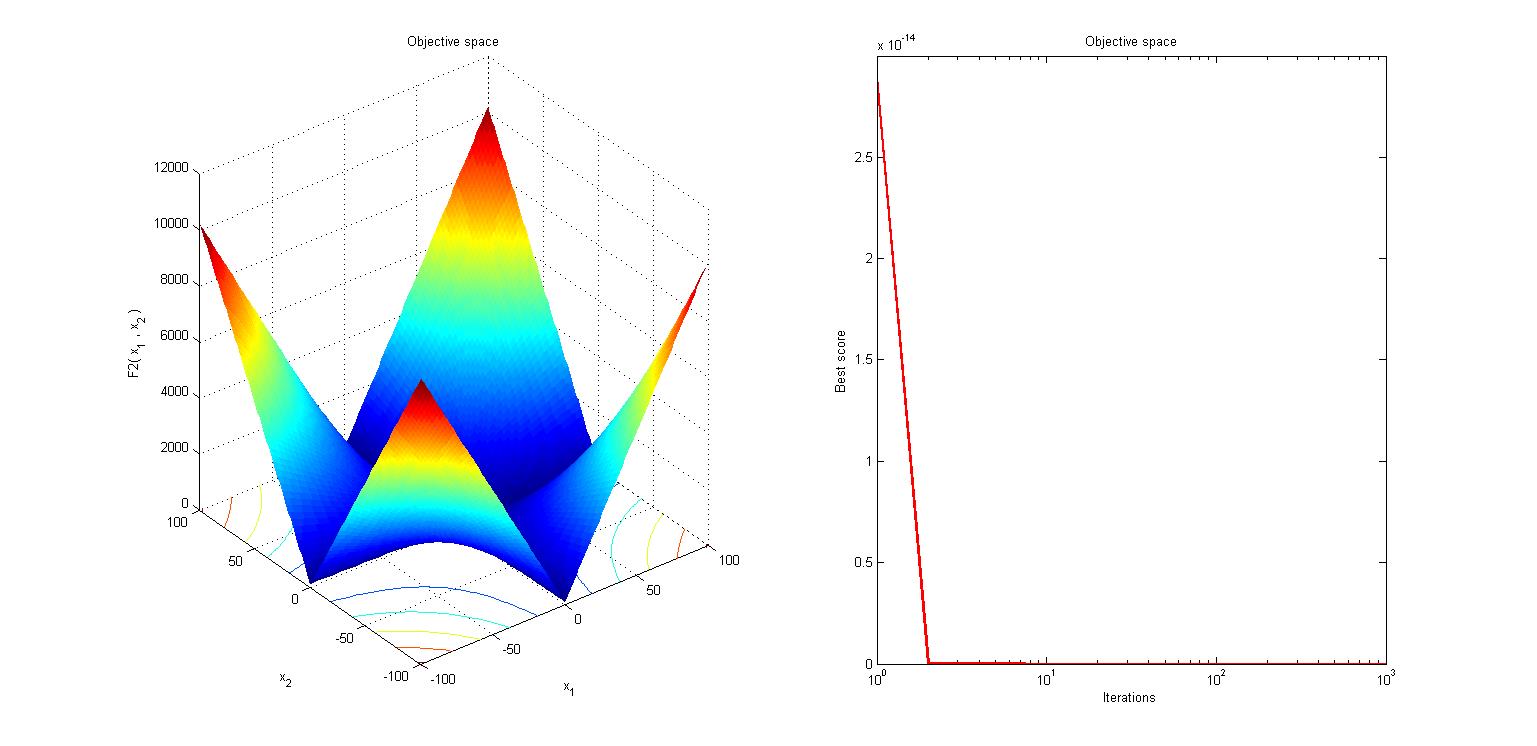
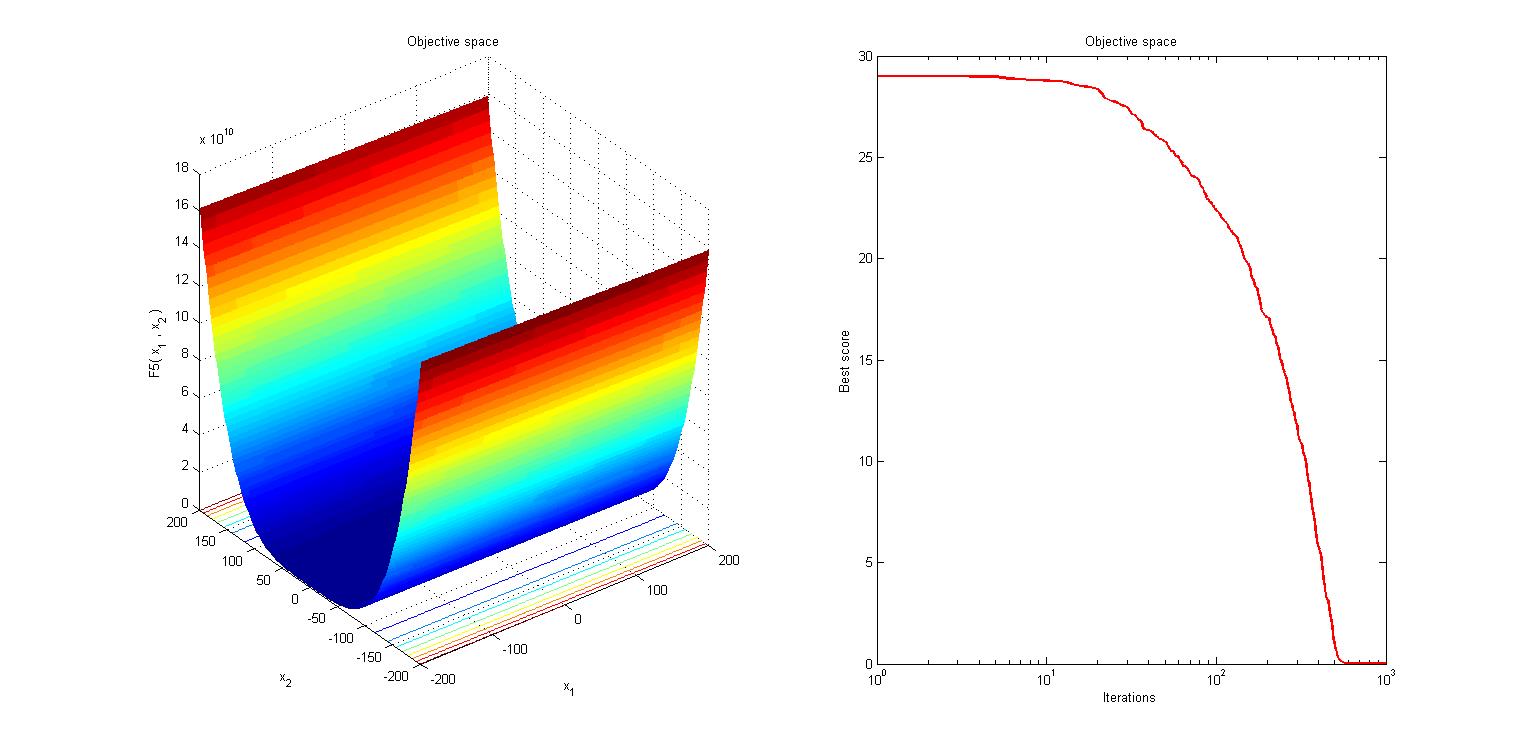
四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]贾鹤鸣,姜子超,李瑶.基于改进秃鹰搜索算法的同步优化特征选择[J].控制与决策