图像配准基于matlab Harris+SIFT图像配准含Matlab源码 1532期

Posted 2021-12-22 紫极神光

一、SIFT配准简介

SIFT即尺度不变特征变换，是用于图像处理领域的一种描述。这种描述具有尺度不变性，可在图像中检测出关键点，是一种局部特征描述子。
1 SIFT算法特点：
（1）具有较好的稳定性和不变性，能够适应旋转、尺度缩放、亮度的变化，能在一定程度上不受视角变化、仿射变换、噪声的干扰。
（2）区分性好，能够在海量特征数据库中进行快速准确的区分信息进行匹配
（3）多量性，就算只有单个物体，也能产生大量特征向量
（4）高速性，能够快速的进行特征向量匹配
（5）可扩展性，能够与其它形式的特征向量进行联合

2 SIFT算法实质
在不同的尺度空间上查找关键点，并计算出关键点的方向。

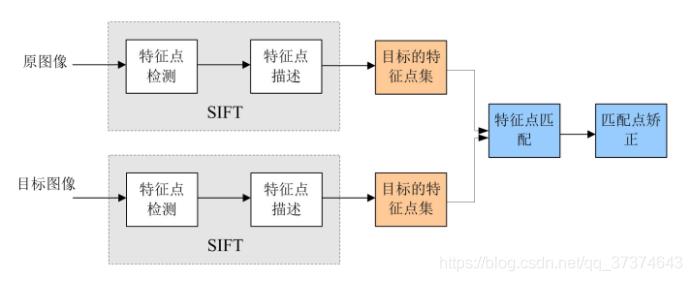
3 SIFT算法实现特征匹配主要有以下三个流程：
（1）提取关键点：关键点是一些十分突出的不会因光照、尺度、旋转等因素而消失的点，比如角点、边缘点、暗区域的亮点以及亮区域的暗点。此步骤是搜索所有尺度空间上的图像位置。通过高斯微分函数来识别潜在的具有尺度和旋转不变的兴趣点。
（2）定位关键点并确定特征方向：在每个候选的位置上，通过一个拟合精细的模型来确定位置和尺度。关键点的选择依据于它们的稳定程度。然后基于图像局部的梯度方向，分配给每个关键点位置一个或多个方向。所有后面的对图像数据的操作都相对于关键点的方向、尺度和位置进行变换，从而提供对于这些变换的不变性。
（3）通过各关键点的特征向量，进行两两比较找出相互匹配的若干对特征点，建立景物间的对应关系。

4 尺度空间
（1）概念
尺度空间即试图在图像领域中模拟人眼观察物体的概念与方法。例如：观察一颗树，关键在于我们想要观察是树叶子还是整棵树：如果是一整棵树(相当于大尺度情况下观察)，那么就应该去除图像的细节部分。如果是树叶(小尺度情况下观察)，那么就该观察局部细节特征。
SIFT算法在构建尺度空间时候采取高斯核函数进行滤波，使原始图像保存最多的细节特征，经过高斯滤波后细节特征逐渐减少来模拟大尺度情况下的特征表示。
利用高斯核函数进行滤波的主要原因有两个：
a 高斯核函数是唯一的尺度不变核函数。
b DoG核函数可以近似为LoG函数，这样可以使特征提取更加简单。同时，David. Lowe作者在论文中提出将原始图像进行2倍上采样后滤波能够保留更多的信息便于后续特征提取与匹配。其实尺度空间图像生成就是当前图像与不同尺度核参数σ进行卷积运算后产生的图像。
（2）表示
L(x, y, σ) ,定义为原始图像 I(x, y)与一个可变尺度的2维高斯函数G(x, y, σ) 卷积运算。

5 高斯金字塔的构建
（1）概念
尺度空间在实现时使用高斯金字塔表示，高斯金字塔的构建分为两步：
a 对图像做高斯平滑；
b 对图像做降采样。

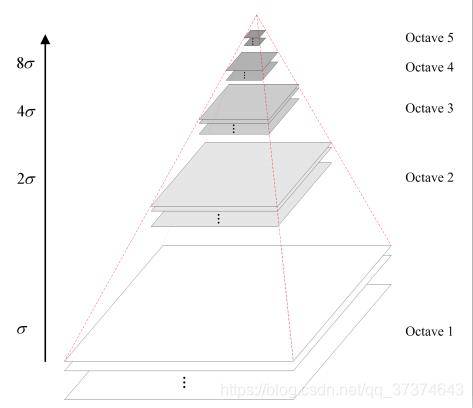
图像的金字塔模型是指将原始图像不断降阶采样，得到一系列大小不一的图像，由大到小，从下到上构成的塔状模型。原图像为金子塔的第一层，每次降采样所得到的新图像为金字塔的一层(每层一张图像)，每个金字塔共n层。为了让尺度体现其连续性，高斯金字塔在简单降采样的基础上加上了高斯滤波。如上图所示，将图像金字塔每层的一张图像使用不同参数做高斯模糊，Octave表示一幅图像可产生的图像组数，Interval表示一组图像包括的图像层数。另外，降采样时，高斯金字塔上一组图像的初始图像(底层图像)是由前一组图像的倒数第三张图像隔点采样得到的。
（2）表示
高斯图像金字塔共o组、s层，则有

6 DOG空间极值检测
（1）DOG函数

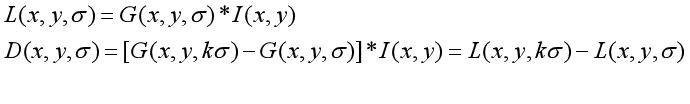
（2）DoG高斯差分金字塔
a 对应DOG算子，需构建DOG金字塔。
可以通过高斯差分图像看出图像上的像素值变化情况。（如果没有变化，也就没有特征。特征必须是变化尽可能多的点。）DOG图像描绘的是目标的轮廓。

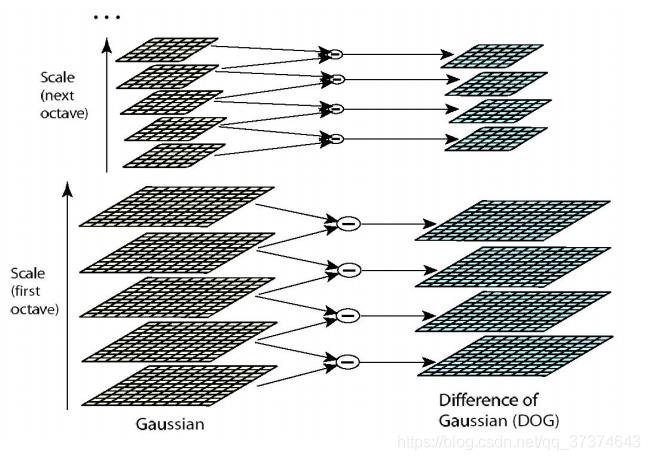
b DOG局部极值检测
特征点是由DOG空间的局部极值点组成的。为了寻找DoG函数的极值点，每一个像素点要和它所有的相邻点比较，看其是否比它的图像域和尺度域的相邻点大或者小。特征点是由DOG空间的局部极值点组成的。为了寻找DoG函数的极值点，每一个像素点要和它所有的相邻点比较，看其是否比它的图像域和尺度域的相邻点大或者小。如下图，中间的检测点和它同尺度的8个相邻点和上下相邻尺度对应的9×2个点共26个点比较，以确保在尺度空间和二维图像空间都检测到极值点。

b 去除边缘效应
在边缘梯度的方向上主曲率值比较大，而沿着边缘方向则主曲率值较小。候选特征点的DoG函数D(x)的主曲率与2×2Hessian矩阵H的特征值成正比。


7 关键点方向分配
（1）通过尺度不变性求极值点，需要利用图像的局部特征为给每一个关键点分配一个基准方向，使描述子对图像旋转具有不变性。对于在DOG金字塔中检测出的关键点，采集其所在高斯金字塔图像3σ邻域窗口内像素的梯度和方向分布特征。梯度的模值和方向如下：

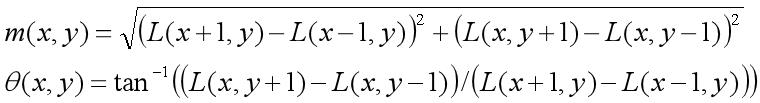
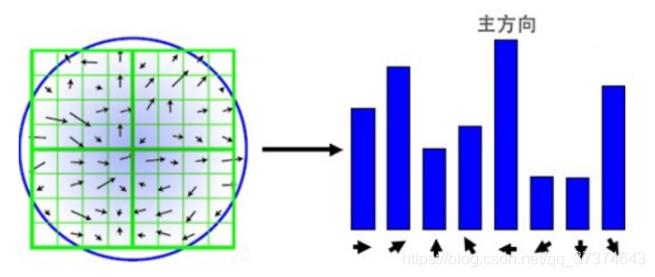
（2）本算法采用梯度直方图统计法，统计以关键点为原点，一定区域内的图像像素点确定关键点方向。在完成关键点的梯度计算后，使用直方图统计邻域内像素的梯度和方向。梯度直方图将0~360度的方向范围分为36个柱，其中每柱10度。如下图所示，直方图的峰值方向代表了关键点的主方向，方向直方图的峰值则代表了该特征点处邻域梯度的方向，以直方图中最大值作为该关键点的主方向。为了增强匹配的鲁棒性，只保留峰值大于主方向峰值80％的方向作为该关键点的辅方向。

8 关键点描述
对于每一个关键点，都拥有位置、尺度以及方向三个信息。为每个关键点建立一个描述符，用一组向量将这个关键点描述出来，使其不随各种变化而改变，比如光照变化、视角变化等等。这个描述子不但包括关键点，也包含关键点周围对其有贡献的像素点，并且描述符应该有较高的独特性，以便于提高特征点正确匹配的概率。

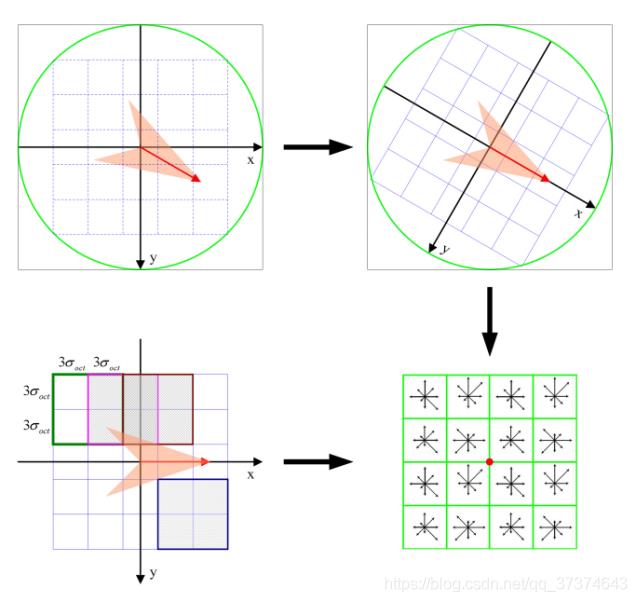
Lowe实验结果表明：描述子采用4×4×8＝128维向量表征，综合效果最优（不变性与独特性）。

9 关键点匹配
（1）分别对模板图（参考图，reference image）和实时图（观测图，
observation image）建立关键点描述子集合。目标的识别是通过两点集内关键点描述子的比对来完成。具有128维的关键点描述子的相似性度量采用欧式距离。
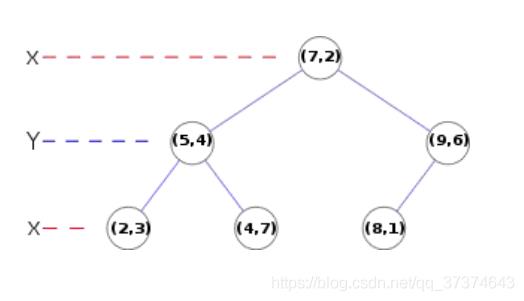
（3）匹配可采取穷举法完成，但所花费的时间太多。所以一般采用kd树的数据结构来完成搜索。搜索的内容是以目标图像的关键点为基准，搜索与目标图像的特征点最邻近的原图像特征点和次邻近的原图像特征点。
Kd树如下如所示，是个平衡二叉树

10 总结
SIFT特征具有稳定性和不变性，在图像处理和计算机视觉领域有着很重要的作用，其本身也是非常复杂的，由于接触SIFT不是很久，对其中的相关知识了解还很不足，经多方查阅参考，写得此文，内容还不够详尽，望多多见谅。以下是SIFT算法的粗略总结。
（1）DoG尺度空间的极值检测。
（2）删除不稳定的极值点。
（3）确定特征点的主方向
（4）生成特征点的描述子进行关键点匹配。

二、部分源代码

%Image Stitching assignment

img1=imread('1.jpg');

%set this image as the reference image.
ref_img2=imread('2.jpg');

img3=imread('3.jpg');

% find homography between img1 and ref image img2
%use harris and stephens corner detector to get the loacl features of the image.
[ref_a,ref_b,ref_c]=harris(ref_img2);
[a1,b1,c1]=harris(img1);
[a2,b2,c2]=harris(img3);
% now use the SIFT decriptor to get the descriptors of both the image 
% Only scale invariant not rotational invariant. Not needed for this
% assignment.
%find circles for ref and img_1
%radius of ref_img
radius_ref=repmat(3,[size(ref_c),1]);
%radius of img_1;
radius_img1=repmat(3,[size(c1),1]);
%radius of img3
radius_img3=repmat(3,[size(c2),1]);
%create a circle array of N*3 size for repmat


%use sift descriptors
sift_desc_ref=find_sift(ref_img2,ref_circle,2);
sift_desc_img1=find_sift(img1,img1_circle,2);
sift_desc_img2=find_sift(img3,img3_circle,2);   
%Match features between two images.
%use the dist2 function two find the 2-nearest neighbors
dist_ref_img1=dist2(sift_desc_ref,sift_desc_img1);
dist_ref_img2=dist2(sift_desc_ref,sift_desc_img2);

[row, col]=size(dist_ref_img1);
[row1, col1]=size(dist_ref_img2);
%function for matching
[img_ref,image_cores]=matching_features(row,dist_ref_img1,ref_circle,img1_circle,img1);
[img_ref1,image_cores1]=matching_features(row1,dist_ref_img2,ref_circle,img3_circle,img3);
%Plot correspondence
PlotImageCores(img_ref,image_cores,img1);
PlotImageCores(img_ref1,image_cores1,img3);

%Use Ransac to get good amount of inliners.
inliners=RANSAC(img_ref,image_cores);
inliners1=RANSAC(img_ref1,image_cores1);
%Find inliner points for the image
[final_inliner_ref,final_inliner_img]=InlierPoint(img_ref,image_cores,inliners);
[final_inliner_ref1,final_inliner_img1]=InlierPoint(img_ref1,image_cores1,inliners1);

%Plot new inliner correspondence

H_re1=computeH(final_inliner_ref1,final_inliner_img1);
%reproject on the image and do the image stitching 
final_mosaic=Mosaicing(ref_img2,img1,H_re);
final_mosaic=uint8(final_mosaic);
final_mosaic1=Mosaicing(ref_img2,img3,H_re1);
final_mosaic1=uint8(final_mosaic1);
final_image=Mosaicing(final_mosaic,final_mosaic1,eye(3));
[rowF,colF,K]=size(final_mosaic);
final_image=zeros(rowF,colF,3);
for i=1:rowF
    for j=1:colF
        for k=1:K
            if final_mosaic(i,j,k)>final_mosaic1(i,j,k)
                final_image(i,j,k)=final_mosaic(i,j,k);
            elseif final_mosaic(i,j,k)<final_mosaic1(i,j,k)
                final_image(i,j,k)=final_mosaic1(i,j,k);
            elseif final_mosaic(i,j,k)==final_mosaic1(i,j,k)
                final_image(i,j,k)=final_mosaic(i,j,k);
            end
        end
    end
end
figure;
imshow(uint8(final_image),'InitialMagnification','fit');
title('全景图');



figure;
imshow(uint8(final_image),'InitialMagnification','fit');
title('频域低通滤波后的全景图');
function sift_arr = find_sift(I, circles, enlarge_factor)
%%
%% Compute non-rotation-invariant SIFT descriptors of a set of circles 
%% I is the image
%% circles is an Nx3 array where N is the number of circles, where the
%%    first column is the x-coordinate (column), the second column is the y-coordinate (row),
%%    and the third column is the radius
%% enlarge_factor is by how much to enarge the radius of the circle before
%%    computing the descriptor (a factor of 1.5 or larger is usually necessary
%%    for best performance)
%% The output is an Nx128 array of SIFT descriptors
%% (c) Lana Lazebnik
%%

if ndims(I) == 3
    I = im2double(rgb2gray(I));
else
    I = im2double(I);
end


fprintf('Running find_sift\\n');

% parameters (default SIFT size)
num_angles = 8;
num_bins = 4;
num_samples = num_bins * num_bins;
alpha = 9; % smoothing for orientation histogram

if nargin < 3
    enlarge_factor = 1.5;
end

angle_step = 2 * pi / num_angles;
angles = 0:angle_step:2*pi;
angles(num_angles+1) = []; % bin centers

[hgt wid] = size(I);
num_pts = size(circles,1);

sift_arr = zeros(num_pts, num_samples * num_angles);

% edge image
sigma_edge = 1;


[G_X,G_Y]=gen_dgauss(sigma_edge);
I_X = filter2(G_X, I, 'same'); % vertical edges
I_Y = filter2(G_Y, I, 'same'); % horizontal edges
I_mag = sqrt(I_X.^2 + I_Y.^2); % gradient magnitude
I_theta = atan2(I_Y,I_X);
I_theta(isnan(I_theta)) = 0; % necessary????

% make default grid of samples (centered at zero, width 2)
interval = 2/num_bins:2/num_bins:2;
interval = interval - (1/num_bins + 1);
[grid_x grid_y] = meshgrid(interval, interval);
grid_x = reshape(grid_x, [1 num_samples]);
grid_y = reshape(grid_y, [1 num_samples]);

% make orientation images
I_orientation = zeros(hgt, wid, num_angles);
% for each histogram angle
for a=1:num_angles    
    % compute each orientation channel
    tmp = cos(I_theta - angles(a)).^alpha;
    tmp = tmp .* (tmp > 0);
    
    % weight by magnitude
    I_orientation(:,:,a) = tmp .* I_mag;
end

三、运行结果

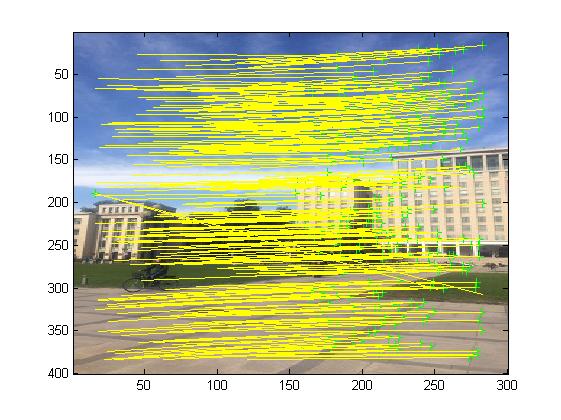
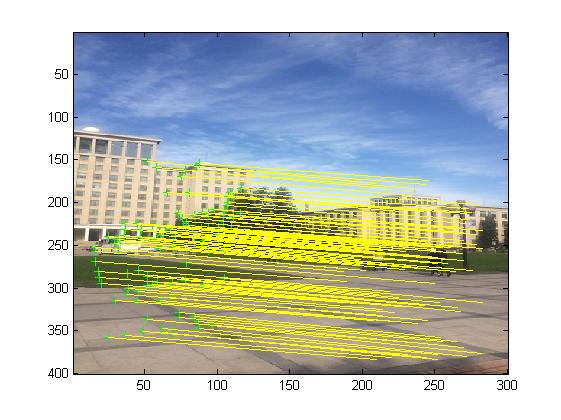
四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 蔡利梅.MATLAB图像处理——理论、算法与实例分析[M].清华大学出版社，2020.
[2]杨丹,赵海滨,龙哲.MATLAB图像处理实例详解[M].清华大学出版社，2013.
[3]周品.MATLAB图像处理与图形用户界面设计[M].清华大学出版社，2013.
[4]刘成龙.精通MATLAB图像处理[M].清华大学出版社，2015.
[5]侯思祖,陈宇,刘雅婷.基于互信息的紫外成像仪中图像配准研究[J].半导体光电. 2020,41(04)