ybtoj 递推二分C. 3.无限序列

Posted 2021-12-22 SSL_ZZL

C. 3.无限序列

• 题面
• 解题思路
• Code

ybtoj 递推 C. 3.无限序列

---

题面

---

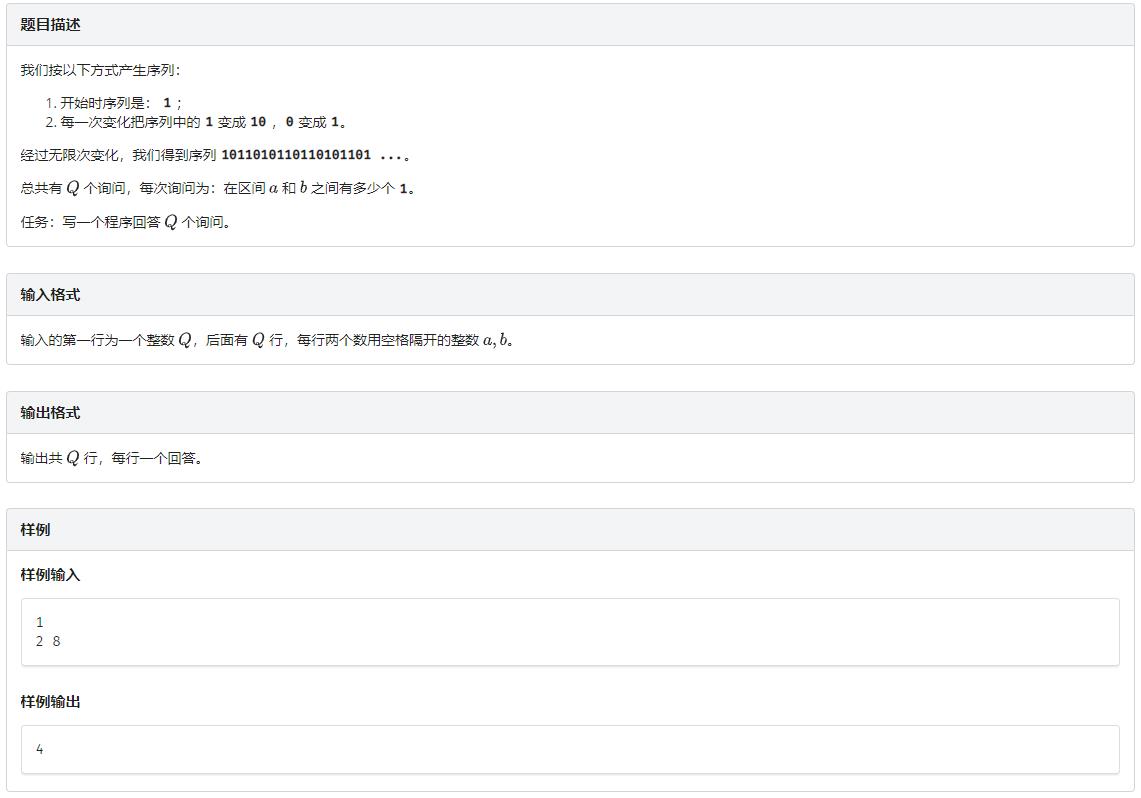
解题思路

$1101011011010110101$
f[i] = f[i - 1] + f[i - 2]

于是题目就变简单了，先算出来 b 长度的数列有多少个1，减去 a-1 长度的数列有多少个 1

因为数列都是由前面的数列拼起来的，所以可以将数列拆开算答案

递推 + 二分查找
比如现在 x = 7

不能找到刚好等于7长度的数列，但是能找到5长度的数列
ans += 3（长度5数列中有3个1）

x = 7 - 5 = 2，有刚好2长度的数列
ans += 1（长度2数列中有1个1）

---

Code

#include <bits/stdc++.h>
#define ll unsigned long long

using namespace std;

ll s[200], vis[200], T, n, m;

void init() 
	s[1] = 1, s[2] = 2;  //长度
	vis[1] = vis[2] = 1;  //有多少个1
	for(int i = 3; i <= 100; i ++) 
		s[i] = s[i - 1] + s[i - 2];
		vis[i] = vis[i - 1] + vis[i - 2];
	


ll find(ll x) 
	if(x == 0) return 0;
	
	int l = 1, r = 100, ans;
	while(l <= r) 
		int mid = (l + r) >> 1;
		if(s[mid] <= x)   //数列尽量覆盖整个x，即长度尽量长，但是要≤x
			ans = mid, l = mid + 1;
		else r = mid - 1;
	
	
	return vis[ans] + find(x - s[ans]);  //剩余一部分


int main() 
	init();
	scanf("%lld", &T);
	while(T --) 
		scanf("%lld %lld", &n, &m);
		printf("%lld\\n", find(m) - find(n - 1));