kaggle赛题：波士顿房价分析

Posted 2021-12-22 尤尔小屋的猫

公众号：尤而小屋
作者：Peter
编辑：Peter

大家好，我是Peter~

这个是Kaggle专栏的第二篇，赛题名是： House Prices - Advanced Regression Techniques。在本文中，你将会学习到：

• 单、多变量分析
• 相关性分析
• 缺失值、异常值处理
• 哑变量转换

原notebook地址：https://www.kaggle.com/pmarcelino/comprehensive-data-exploration-with-python

排名榜

让我们看下排名榜，第一名真的是碾压其他选手呀~所以，今天我们一起看看这个第一名的方案到底是多棒？

数据介绍

这份波士顿房价的数据集有4份数据，训练集train+测试集test+数据集的描述description+提交模板sample

其中训练集有81个特征，1460条数据；测试集81个特征，1459条数据。看下部分属性介绍：

数据EDA

导入模块和数据，并进行数据探索：

导入库

import pandas as pd
import numpy as np
# 绘图相关
import plotly.express as px
import matplotlib.pyplot as plt
import seaborn as sns
plt.style.use("fivethirtyeight")

# 数据建模
from scipy.stats import norm
from scipy import stats
from sklearn.preprocessing import StandardScaler

# 警告
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline

导入数据

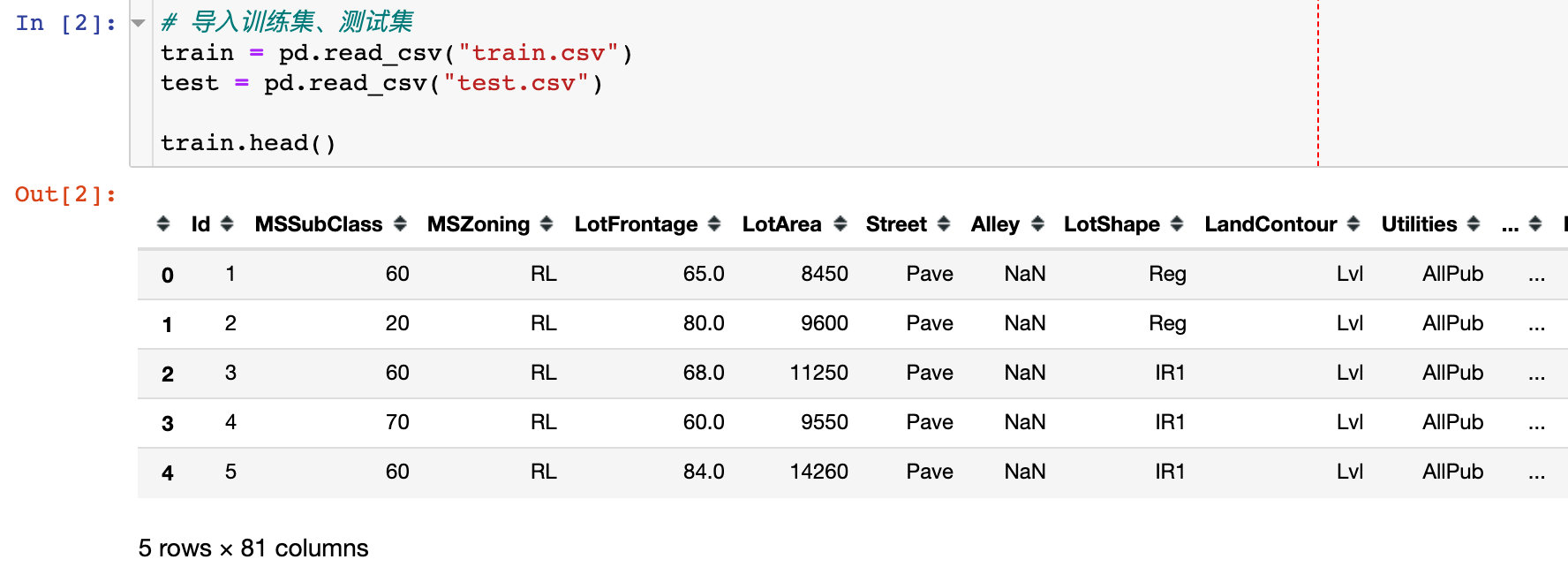
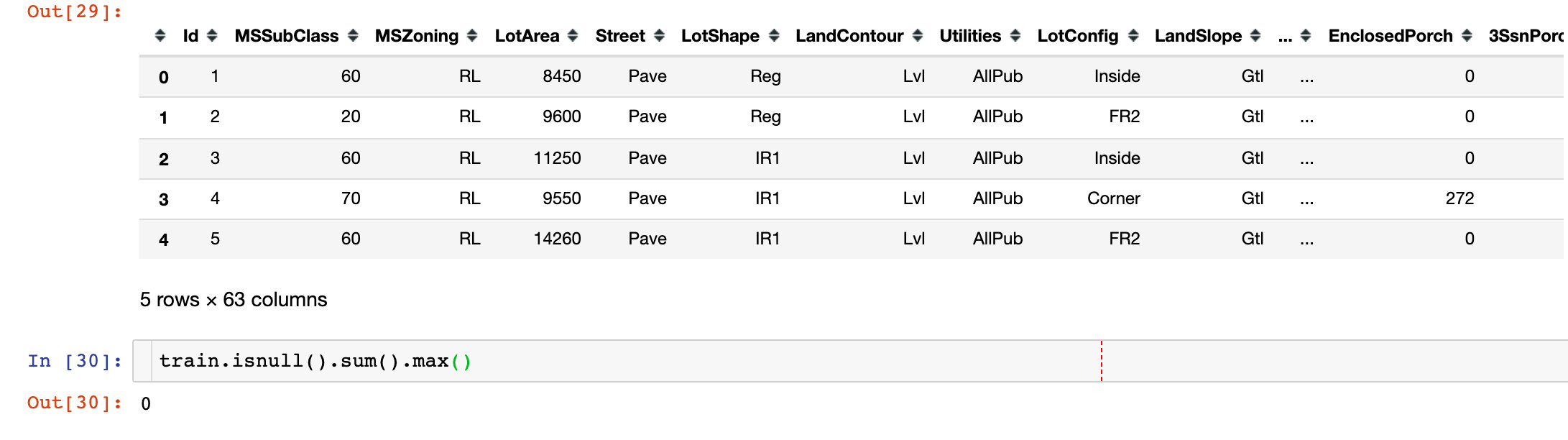
数据信息

训练集整体是1460*81；而且很多的存在字段都存在缺失值

描述统计信息：

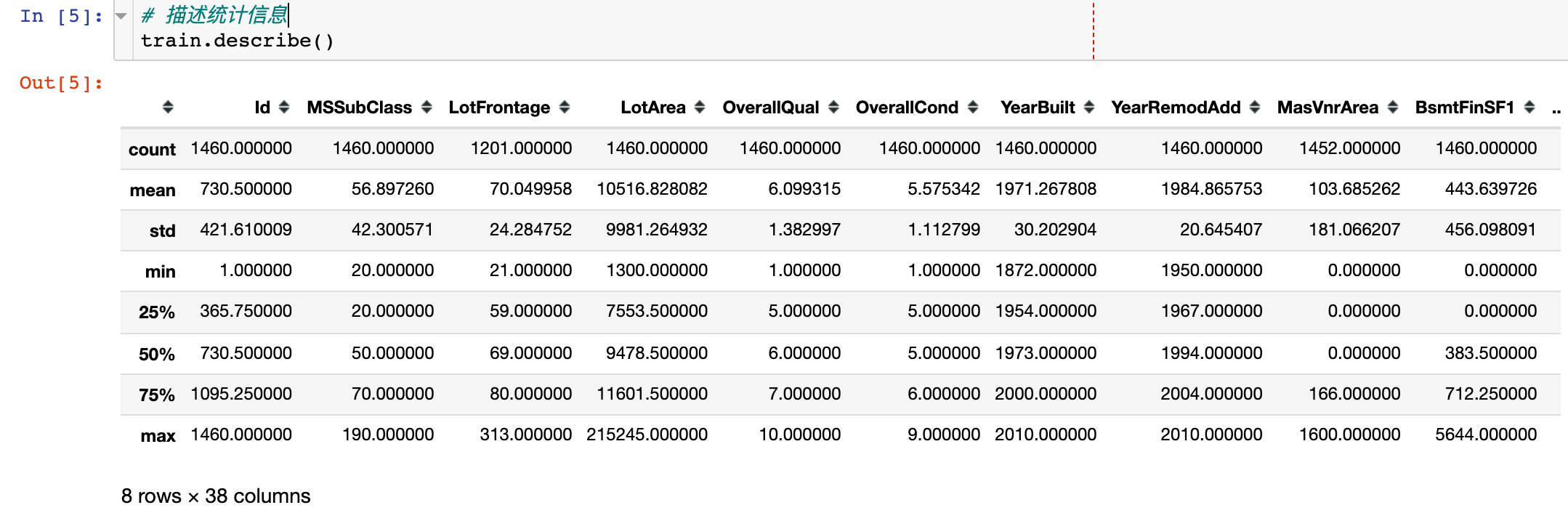
销售价格SalePrice分析

前原notebook文档中，作者分析了很多自己关于这个题目和字段的看法，具体不阐述。下面介绍的是重点部分：

统计信息

单单看这个字段的统计信息：

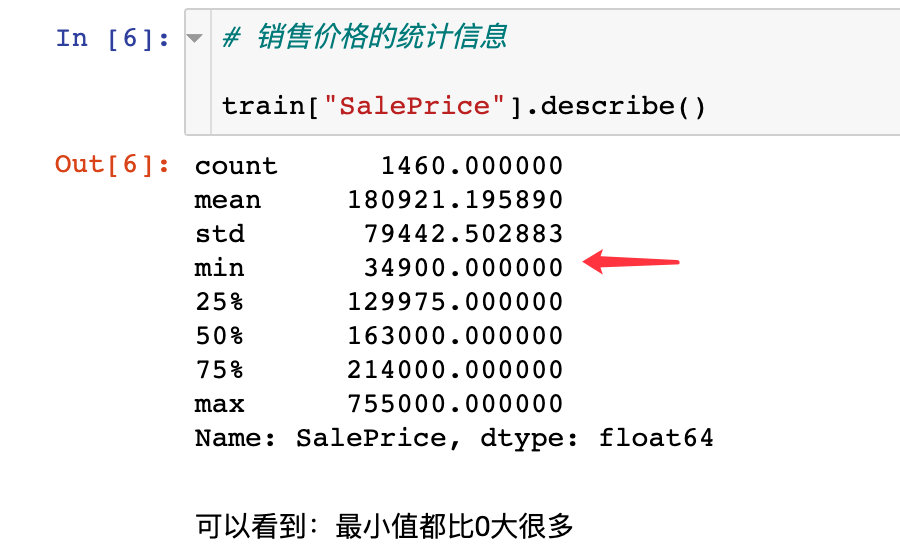
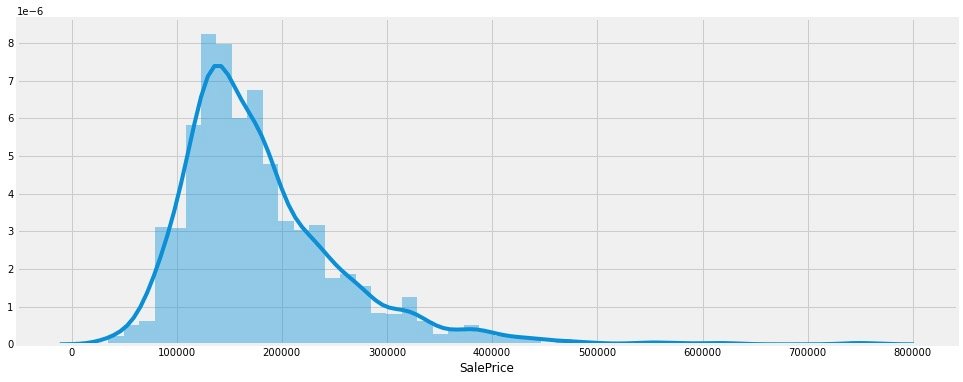
分布直方图如下，我们明显感受到：

• 价格的分布偏离了正态分布
• 有明显的正偏度现象
• 有明显的峰值出现

偏度和峰度（skewness and kurtosis）

知识加油站：偏度和峰度

详细的解释参见文章：https://zhuanlan.zhihu.com/p/53184516

• 偏度：衡量随机变脸概率分布的不对称性，是相对于平均值不对称程度的度量，通过对偏度系数的测量，我们能够判定数据分布的不对称程度以及方向。
• 峰度：是研究数据分布陡峭或者平滑的统计量，通过对峰度系数的测量，我们能够判定数据相对于正态分布而言是更陡峭还是更平缓。峰度接近0，数据呈现正态分布；峰度>0，高尖分布；峰度<0，矮胖分布

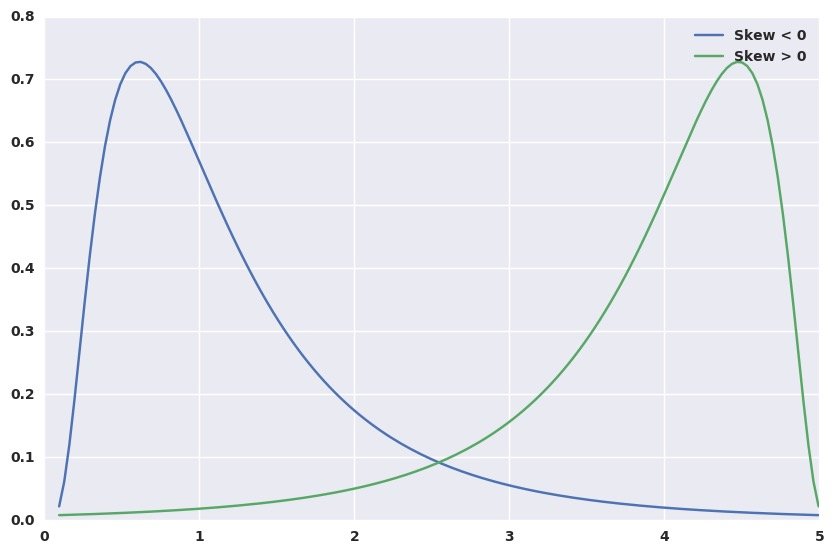
偏度的两种分布情况：

• 如果是左偏，则偏度小于0
• 如果是右偏，则偏度大于0

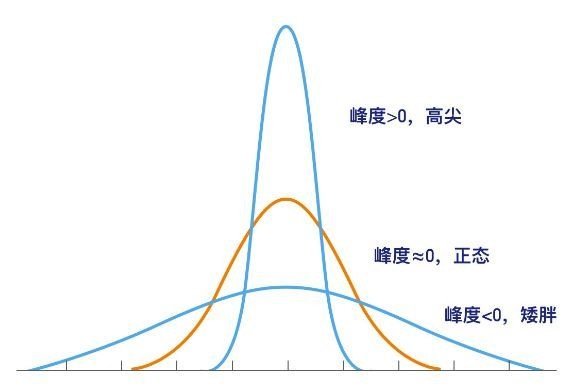
峰度的两种分布情况：

• 如果是高瘦型，则峰度大于0
• 如果是矮胖型，则峰度小于0

# 打印销售价格的偏度和峰度

print("Skewness（偏度）: %f" % train['SalePrice'].skew())
print("Kurtosis（峰度）: %f" % train['SalePrice'].kurt())

Skewness（偏度）: 1.882876
Kurtosis（峰度）: 6.536282

偏度和峰度值都是正的，明显说明数据是右偏且高尖分布

SalePrice和数值型字段的关系

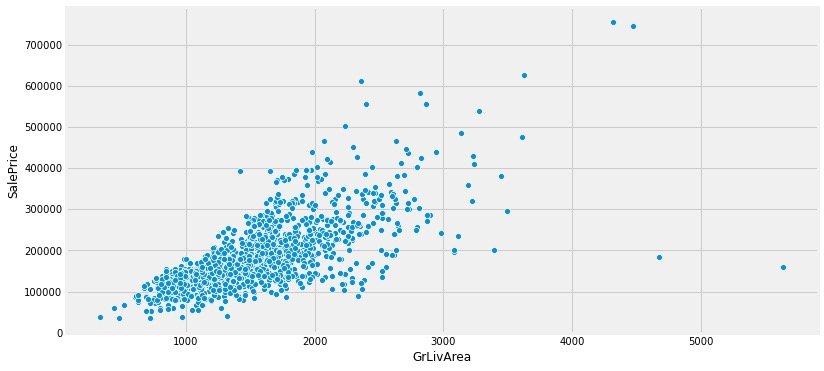
首先我们考察和居住面积的关系：

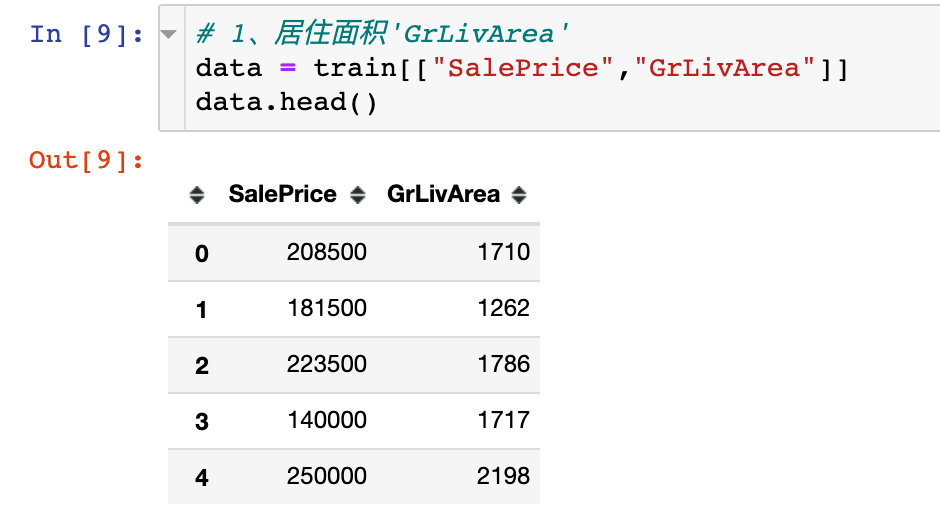
plt.figure(1,figsize=(12,6))
sns.scatterplot(x="GrLivArea",y="SalePrice",data=data)
plt.show()

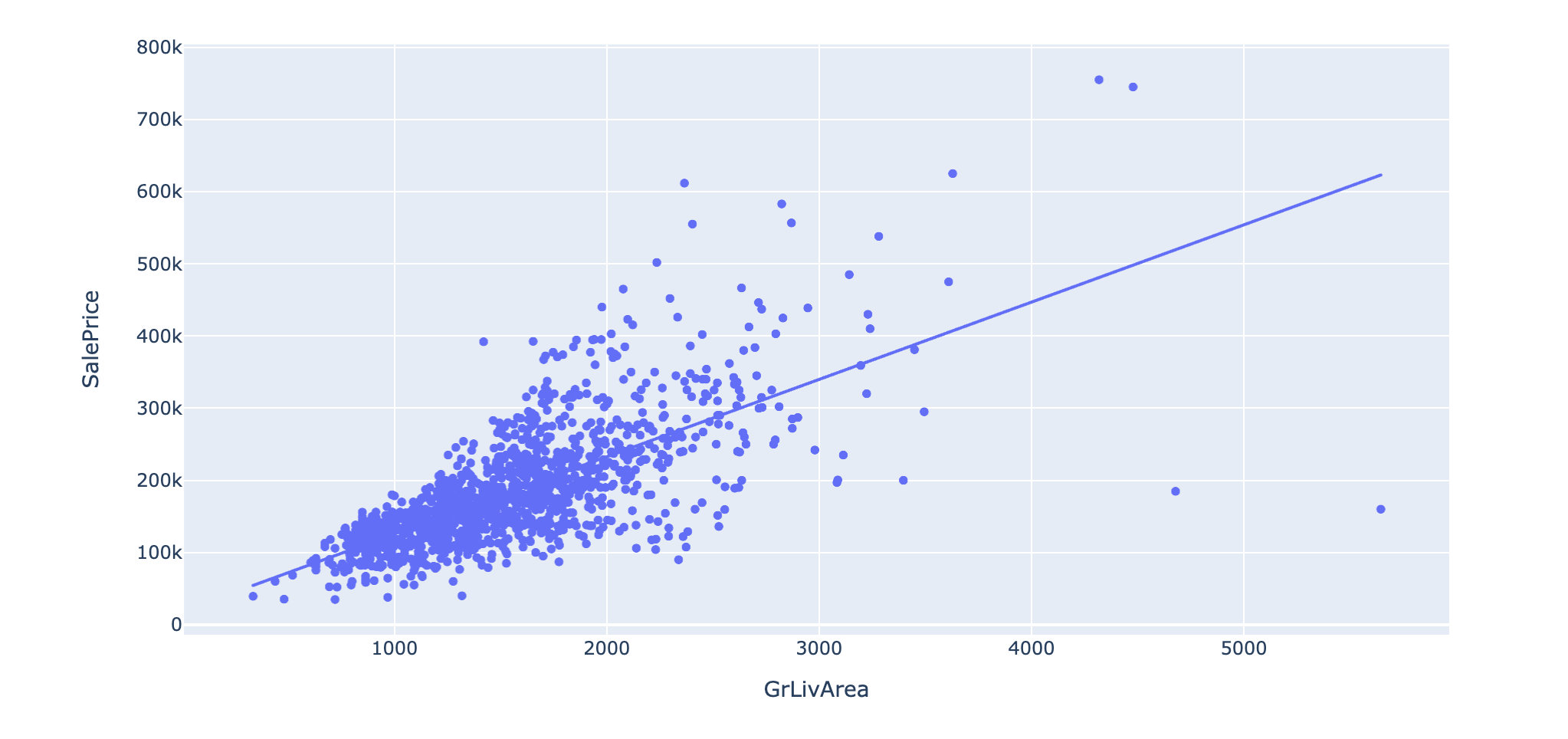
# plotly版本
px.scatter(data,x="GrLivArea",y="SalePrice",trendline="ols")

TotalBsmtSF VS SalePrice

# 2、TotalBsmtSF 
data = train[["SalePrice","TotalBsmtSF"]]

plt.figure(1,figsize=(12,6))
sns.scatterplot(x="TotalBsmtSF",y="SalePrice",data=data)
plt.show()

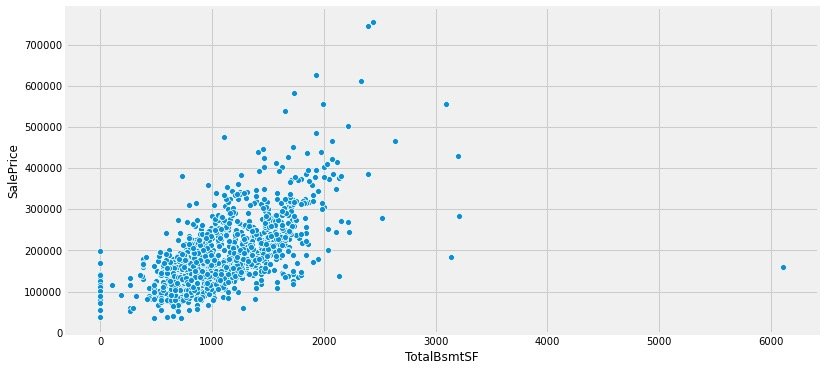
小结：我们可以观察到这两个特征和销售价格之间是存在一定的线性关系。

价格和分类型字段的关系

1、OverallQual VS SalePrice

# 1、OverallQual：整体房屋质量

# 总共10个类别
train["OverallQual"].value_counts()

5     397
6     374
7     319
8     168
4     116
9      43
3      20
10     18
2       3
1       2
Name: OverallQual, dtype: int64

data = train[["SalePrice","OverallQual"]]

# 房屋整体质量和房价的关系
# 绘制子图：1号位
f,ax = plt.subplots(1,figsize=(12,6))
fig = sns.boxplot(x="OverallQual",y="SalePrice",data=data)
# y轴的刻度范围
fig.axis(ymin=0,ymax=800000)
plt.show()

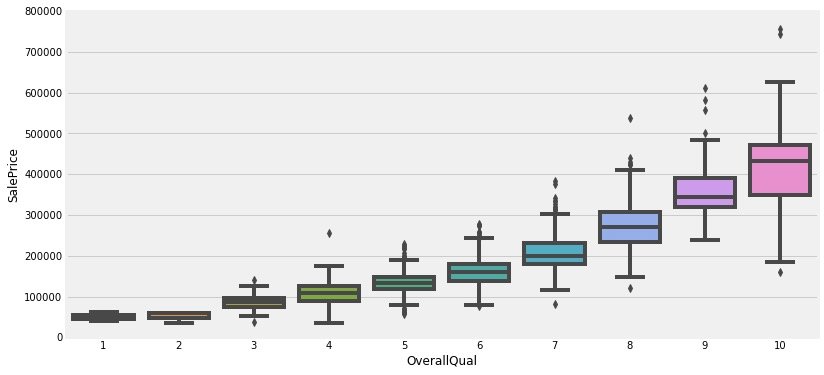
2、YearBuilt VS SalePrice

住在建造年份和销售价格的关系

data = train[["SalePrice","YearBuilt"]]

# 建造年份和房价的关系
f,ax = plt.subplots(1,figsize=(16,8))
fig = sns.boxplot(x="YearBuilt",y="SalePrice",data=data)
# y轴的刻度范围
fig.axis(ymin=0,ymax=800000)
plt.show()

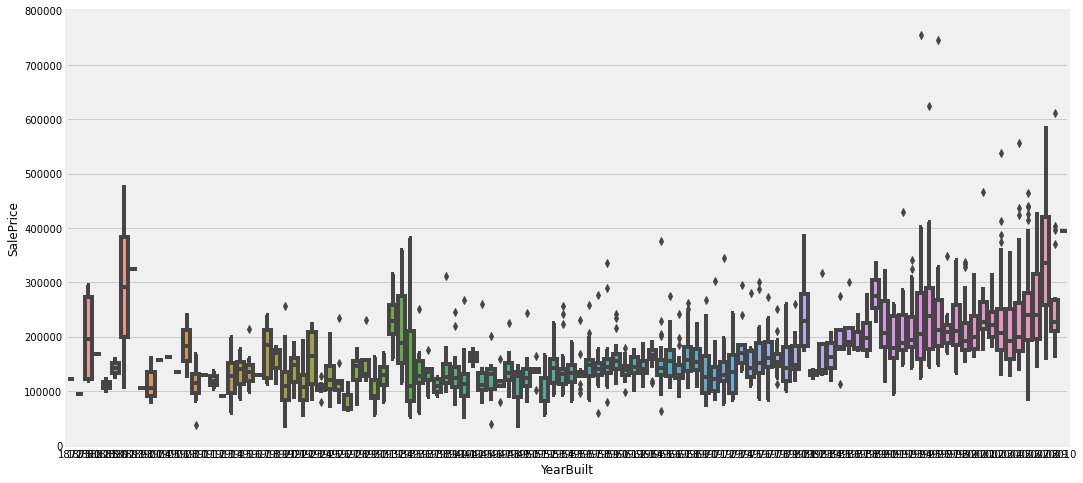
小结：销售价格和住宅的整体质量有很强的关系；但是和建筑年份的关系不大。但是在实际的买房过程中，我们还是会很在意年份

小结

对上面分析的一点小结：

1. 地面生活区(GrLivArea)、地下室面积(GrLivArea)和销售价格SalePrice都是呈现正向的线性相关
2. 房屋的整体质量(OverallQual)和建造年份(YearBuilt)好像也和销售价格线性相关。常识来说，整体的质量越好，价格越贵

相关性分析

为了探索众多属性之间的关系，进行如下的分析：

• 两两属性间的相关性（热力图）
• 销售价格saleprice和其他属性的关系（热力图）
• 关联性最大的属性间的关系（散点图）

整体相关性

分析每两个属性的相关性，并绘制热力图

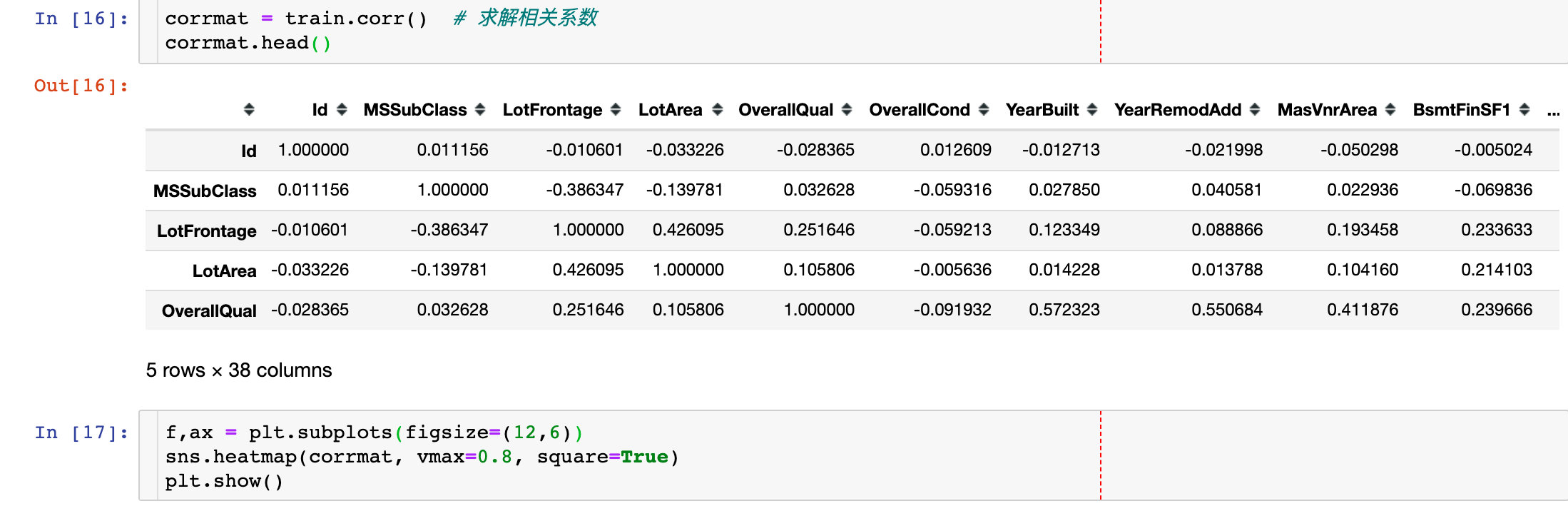
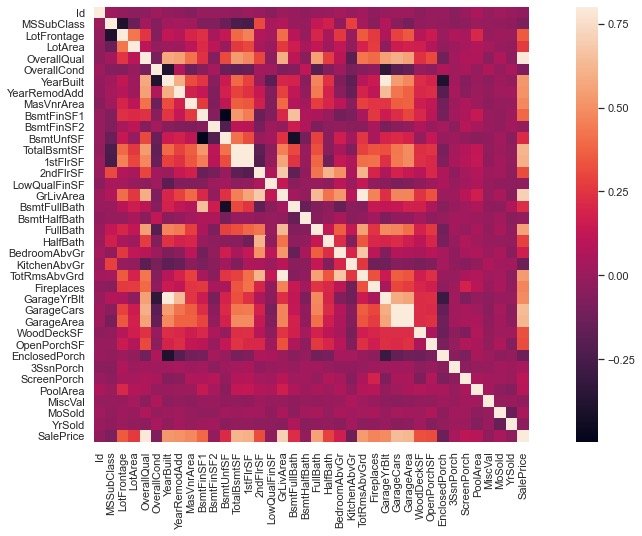
上图中有两个值得关注的点：

• TotalBsmtSF and 1stFlrSF
• GarageCar and GarageArea

这两组变量都是强相关的，我们后续的分析只取其中一个

缩放相关矩阵（销售价格saleprice）

从上面的热力图中选择和SalePrice相关性最强的前10个特征来绘制热力图

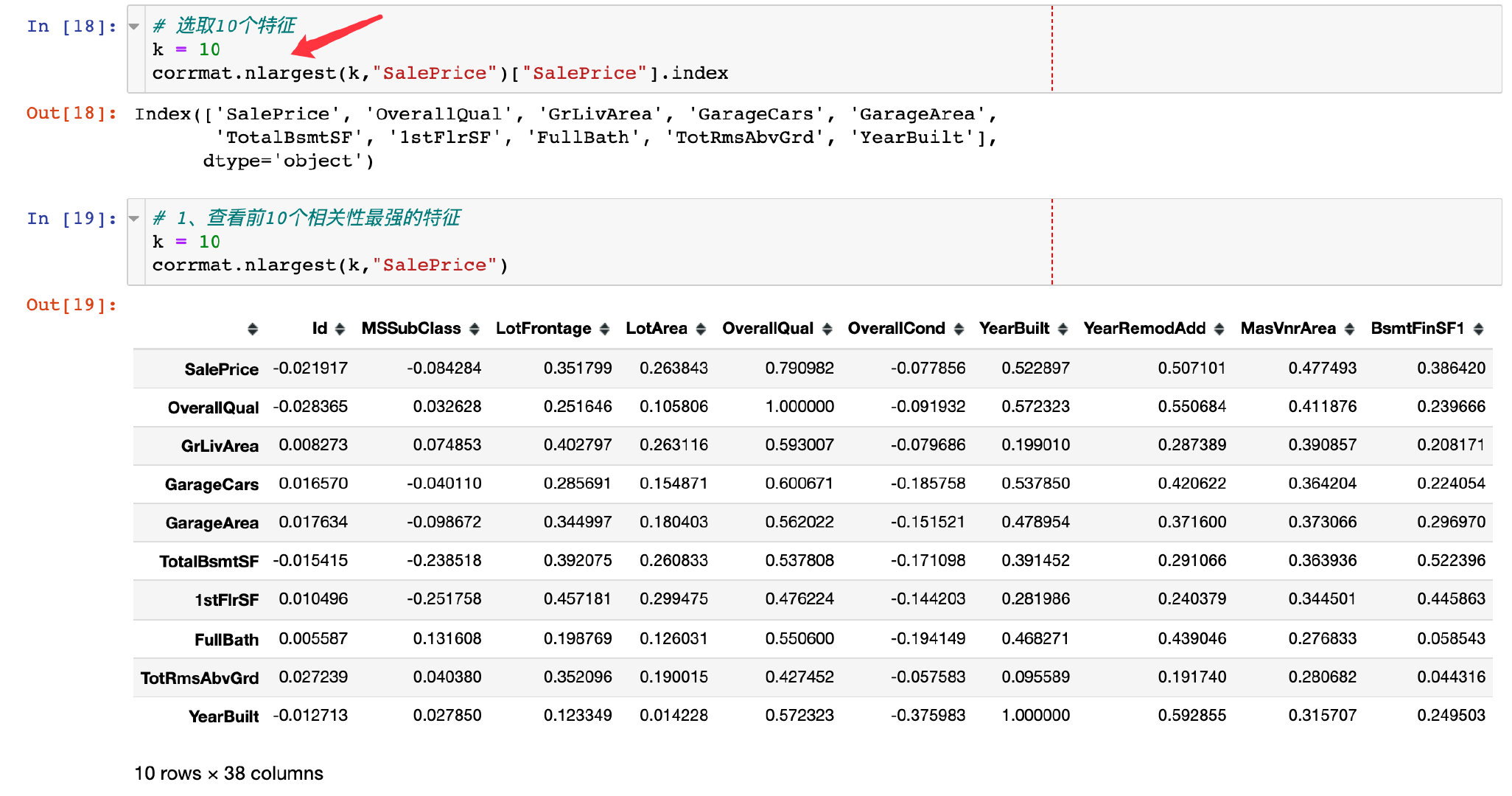
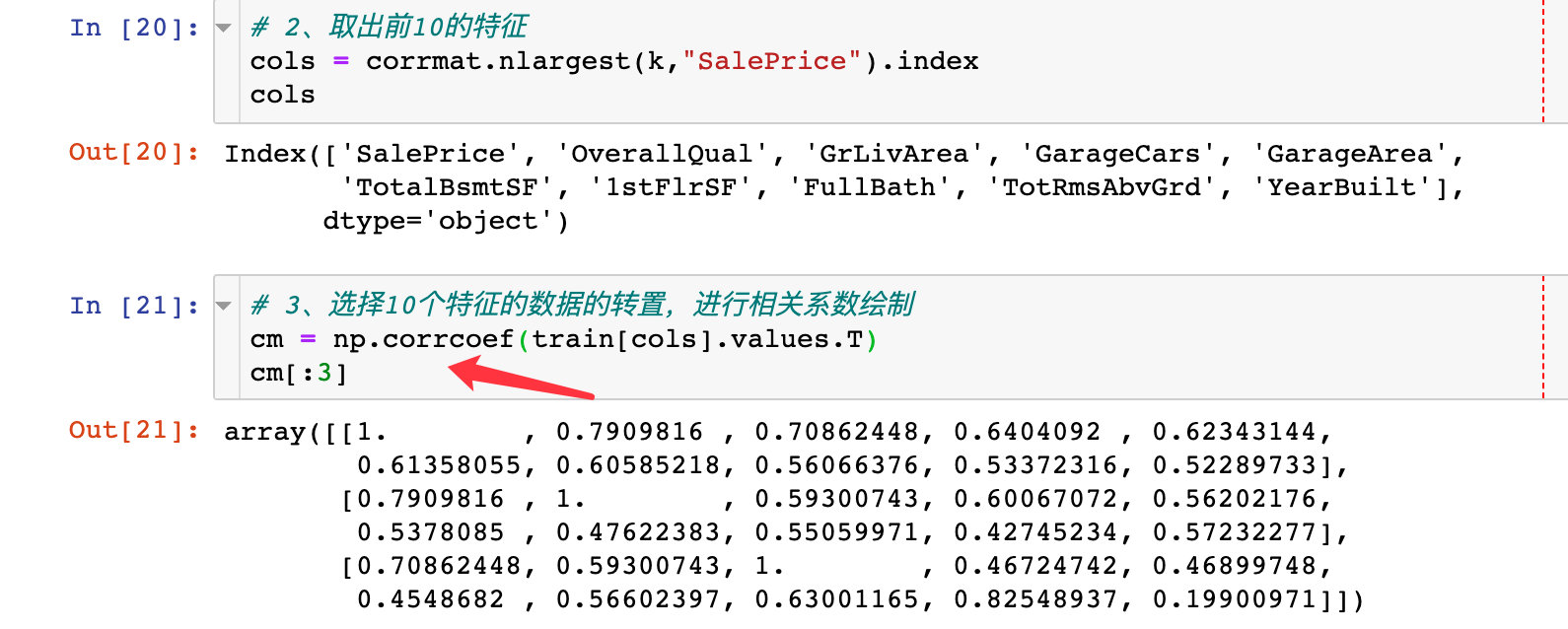
sns.set(font_scale=1.25)
hm = sns.heatmap(
    cm,  # 绘图数据
    cbar=True,  # 是否将颜色条作为图例，默认True
    annot=True,  # 是否显示数值
    square=True,  # 是否使热力图每个单元为正方形，默认为False
    fmt='.2f',  # 保留两位小数
    annot_kws='size':10,
    xticklabels=cols.values, # xy轴设置
    yticklabels=cols.values)

plt.show()

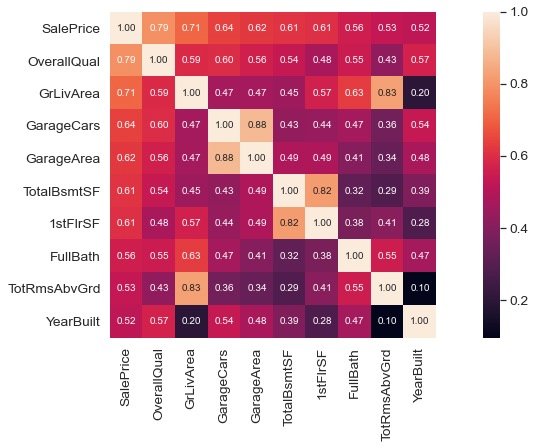
小结1

通过上面的缩放热力图，我们可以得到下面的结论：

• ‘OverallQual’, ‘GrLivArea’ and 'TotalBsmtSF’是真的和’SalePrice’呈现强相关
• ‘GarageCars’ and ‘GarageArea’ 也是两个相关性比较强的特征；而且他们都是同时出现，后续选取GarageCars进行分析
• 建筑年限’YearBuilt’相对来说，相关性比较低

变量离散图

将销售价格SalePrice和几个相关性比较强的特征放在一起，绘制变量离散图

sns.set()
# 待分析的变量
cols = ['SalePrice', 'OverallQual', 'GrLivArea', 'GarageCars', 'TotalBsmtSF', 'FullBath', 'YearBuilt']
sns.pairplot(train[cols],size=2.5)
plt.show()

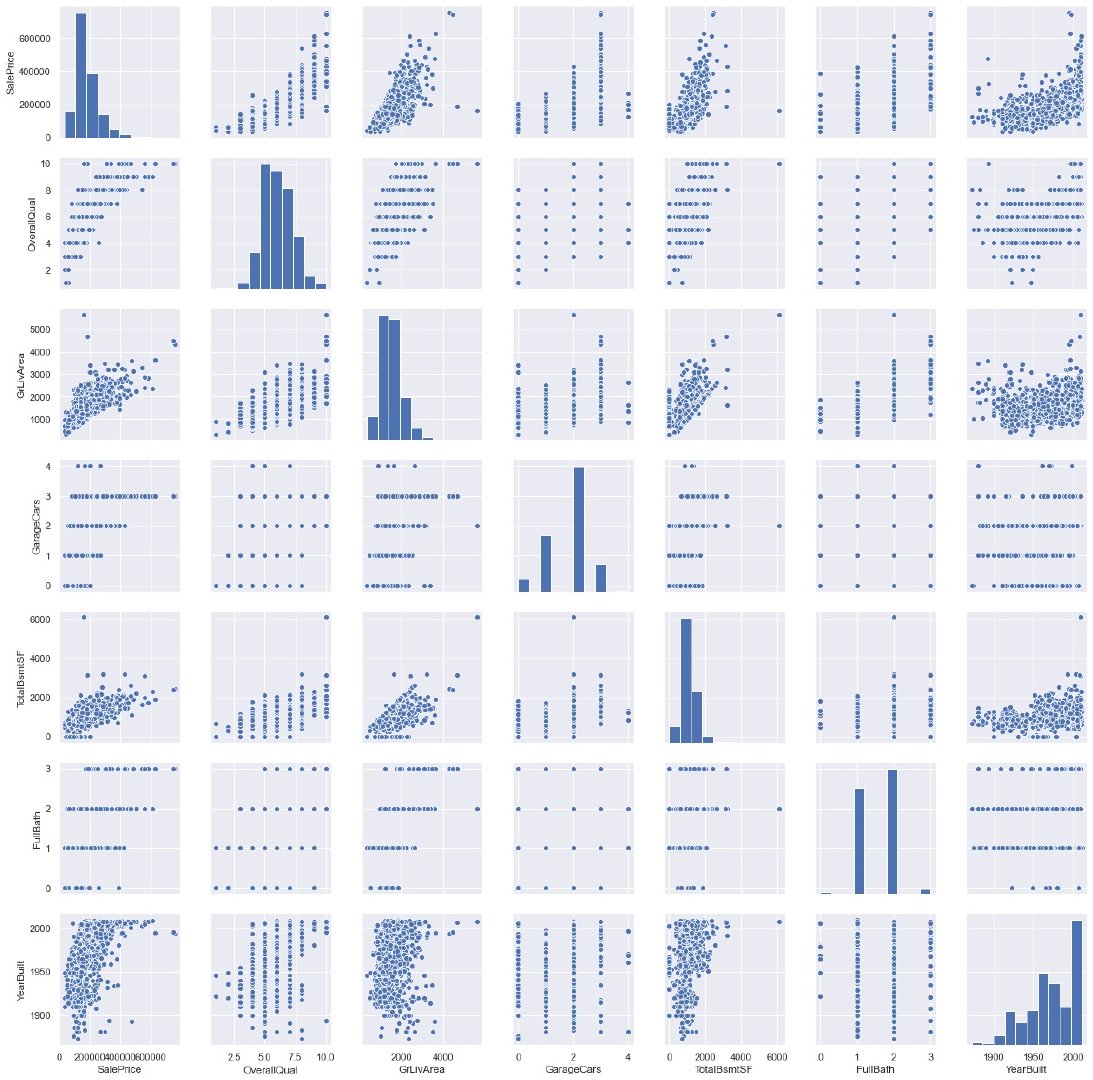
小结2

正对角线方向上是变量的直方图，解释变量和被解释变量SalePrice，其他的则是散点图。

如果图中呈现直线或者横线的散点，则说明该变量是离散的，比如第1行4列的变量，y轴是SalePrice，x轴是YearBuilt，直线说明YearBuilt是离散的

缺失值处理

针对缺失值的情况，主要是讨论两点：

• 缺失值分布情况怎么样？
• 缺失值是随机的？还有具有某种规律

缺失值占比

1、查看每个字段的缺失值情况

# 每个字段的缺失值数量：降序
total = train.isnull().sum().sort_values(ascending=False)
total.head()

PoolQC         1453
MiscFeature    1406
Alley          1369
Fence          1179
FireplaceQu     690
dtype: int64

2、转成百分比

# 每个字段的缺失值 / 总数
percent = (train.isnull().sum() / train.isnull().count()).sort_values(ascending=False)
percent.head()

PoolQC         0.995205
MiscFeature    0.963014
Alley          0.937671
Fence          0.807534
FireplaceQu    0.472603
dtype: float64

3、数据合并，整体的缺失值情况：

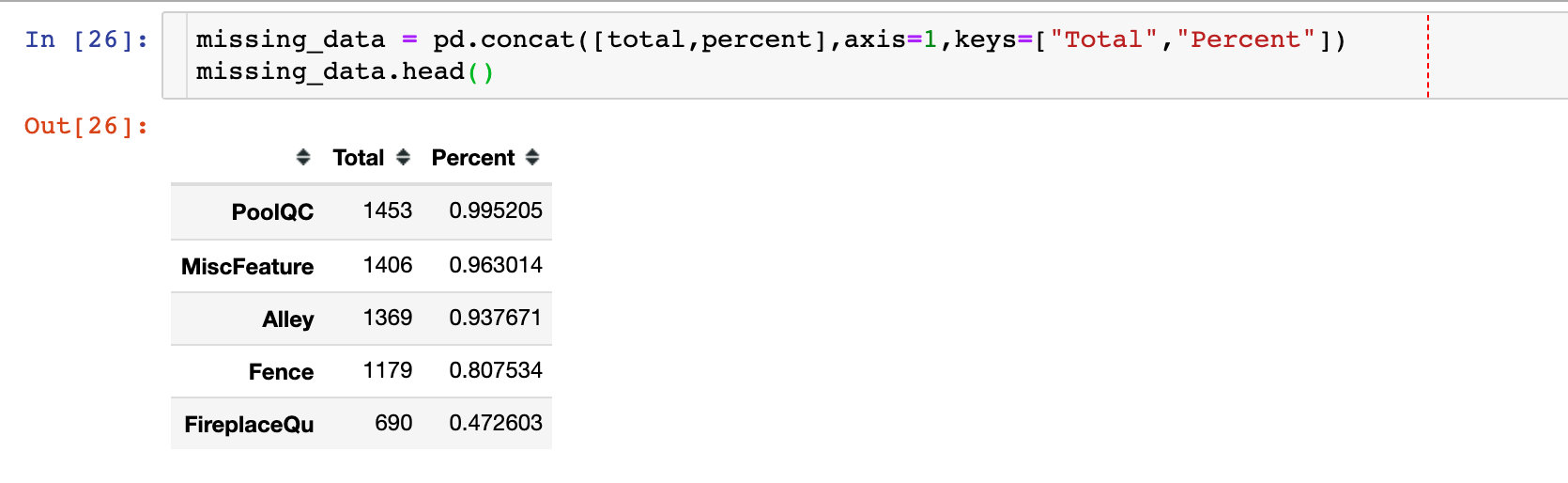
删除缺失值

原文中分析了很多，最后的结论：

In summary, to handle missing data,

1、we’ll delete all the variables with missing data, except the variable ‘Electrical’.

2、In ‘Electrical’ we’ll just delete the observation with missing data.

# 步骤1：需要删除的字段
missing_data[missing_data["Total"] > 1].index

Index(['PoolQC', 'MiscFeature', 'Alley', 'Fence', 'FireplaceQu', 'LotFrontage',
       'GarageYrBlt', 'GarageCond', 'GarageType', 'GarageFinish', 'GarageQual',
       'BsmtFinType2', 'BsmtExposure', 'BsmtQual', 'BsmtCond', 'BsmtFinType1',
       'MasVnrArea', 'MasVnrType'],
      dtype='object')

# 第一步
train = train.drop(missing_data[missing_data["Total"] > 1].index,1)
#	第二步
train = train.drop(train.loc[train["Electrical"].isnull()].index)

离群点out liars

查找离群点

## 数据标准化standardizing data
# np.newaxis 增加数据维度，一维变成二维
saleprice_scaled = StandardScaler().fit_transform(train["SalePrice"][:,np.newaxis])
saleprice_scaled[:5]

array([[ 0.34704187],
       [ 0.0071701 ],
       [ 0.53585953],
       [-0.5152254 ],
       [ 0.86943738]])

# 查看前10和最后10位的数据
# argsort：返回的是索引值；默认是升序排列，最小的在最前面，最大的在最后

low_range = saleprice_scaled[saleprice_scaled[:,0].argsort()][:10]

high_range = saleprice_scaled[saleprice_scaled[:,0].argsort()][-10:]

print(low_range)
print('----------')
print(high_range)

小结3

• low_range接近，且离0比较近
• high_range离0很远；且7+的数据就应该是离群点了

单变量分析1

data = train[["SalePrice","GrLivArea"]]
data.plot.scatter(x="GrLivArea",y="SalePrice",ylim=(0,800000))
plt.show()

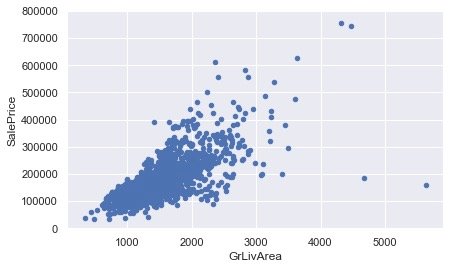
很明显的，两个变量（属性）存在一种线性关系

删除离群点

指定删除某个字段为具体值的方法：

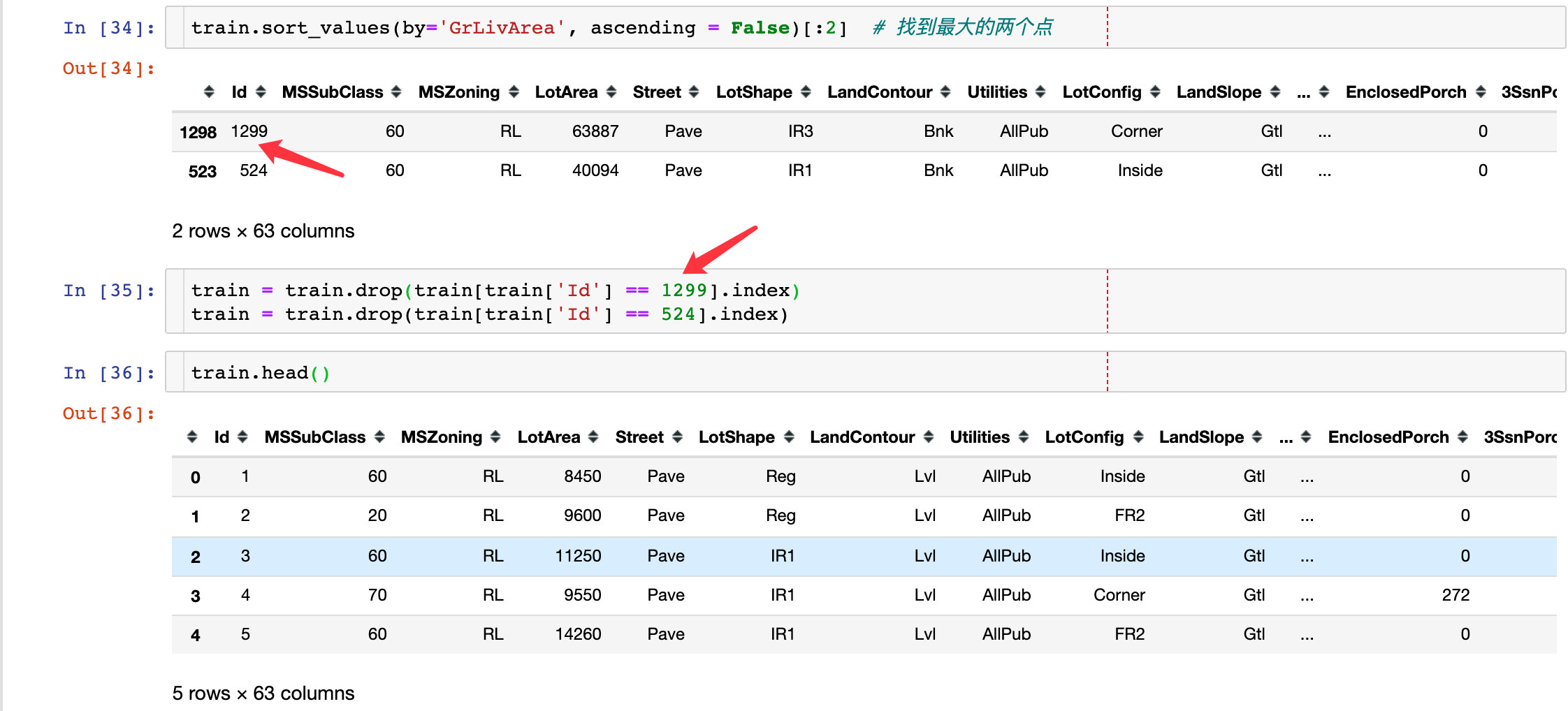
单变量分析2

data = train[["SalePrice","TotalBsmtSF"]]   # 待分析的两个变量
data.plot.scatter(x="TotalBsmtSF",y="SalePrice",ylim=(0,800000))
plt.show()

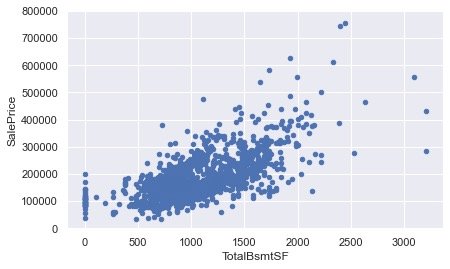
深入理解SalePrice

主要从以下几个方面来深入研究销售价格：

• Normality：归一化
• Homoscedasticity：同方差性
• Linearity：线性特质
• Absence of correlated errors：相关误差

Normality归一化（SalePrice）

sns.distplot(train["SalePrice"],fit=norm)
fig = plt.figure()
res = stats.probplot(train["SalePrice"], plot=plt)

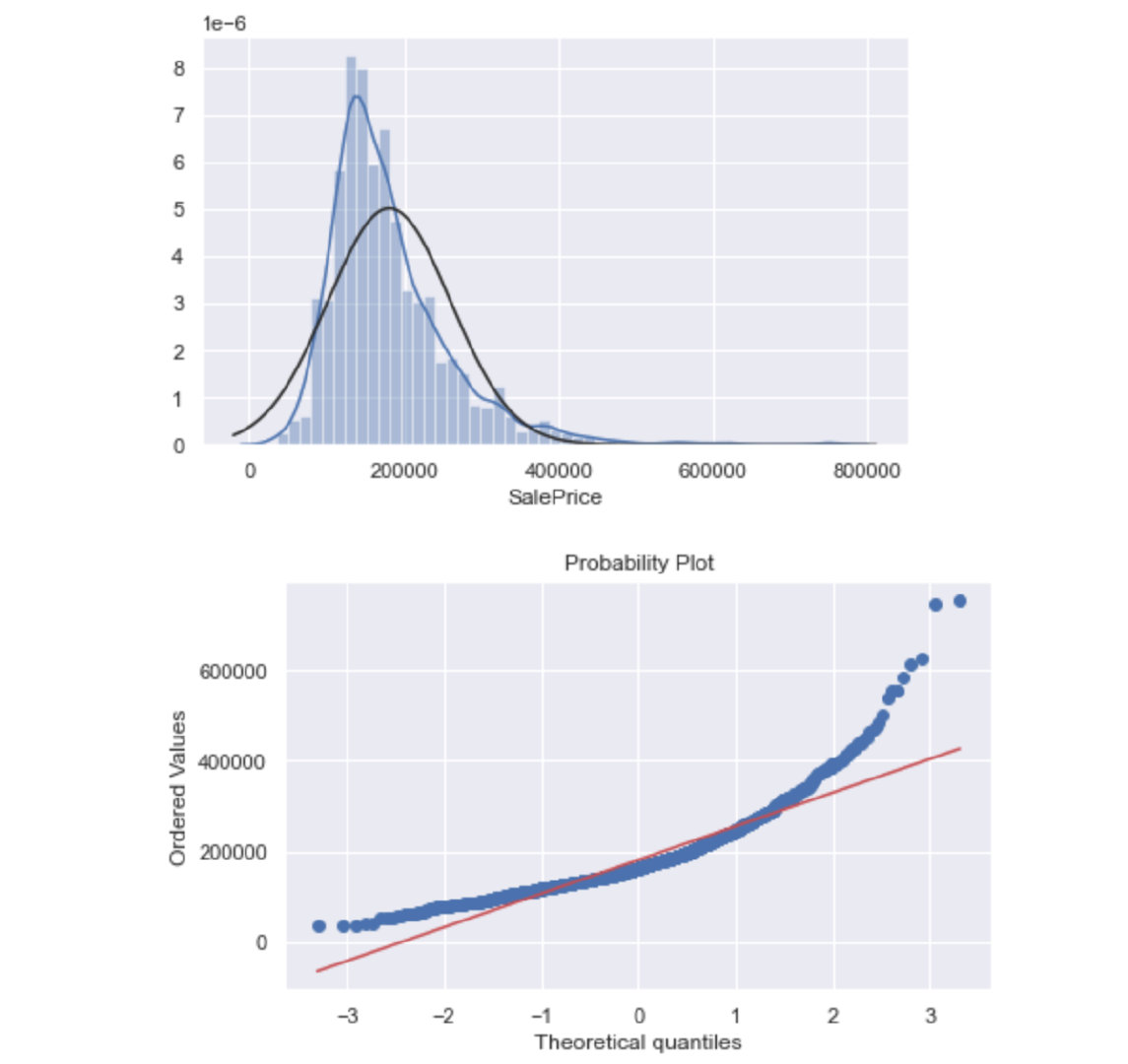
我们发现：销售价格不是正态分布的，出现了右偏度；同时也不遵循对数变化的规律。

为了解决这个问题：实施对数变换

## 对数变换
train["SalePrice"] = np.log(train["SalePrice"])

sns.distplot(train["SalePrice"],fit=norm)
fig = plt.figure()
res = stats.probplot(train["SalePrice"], plot=plt)

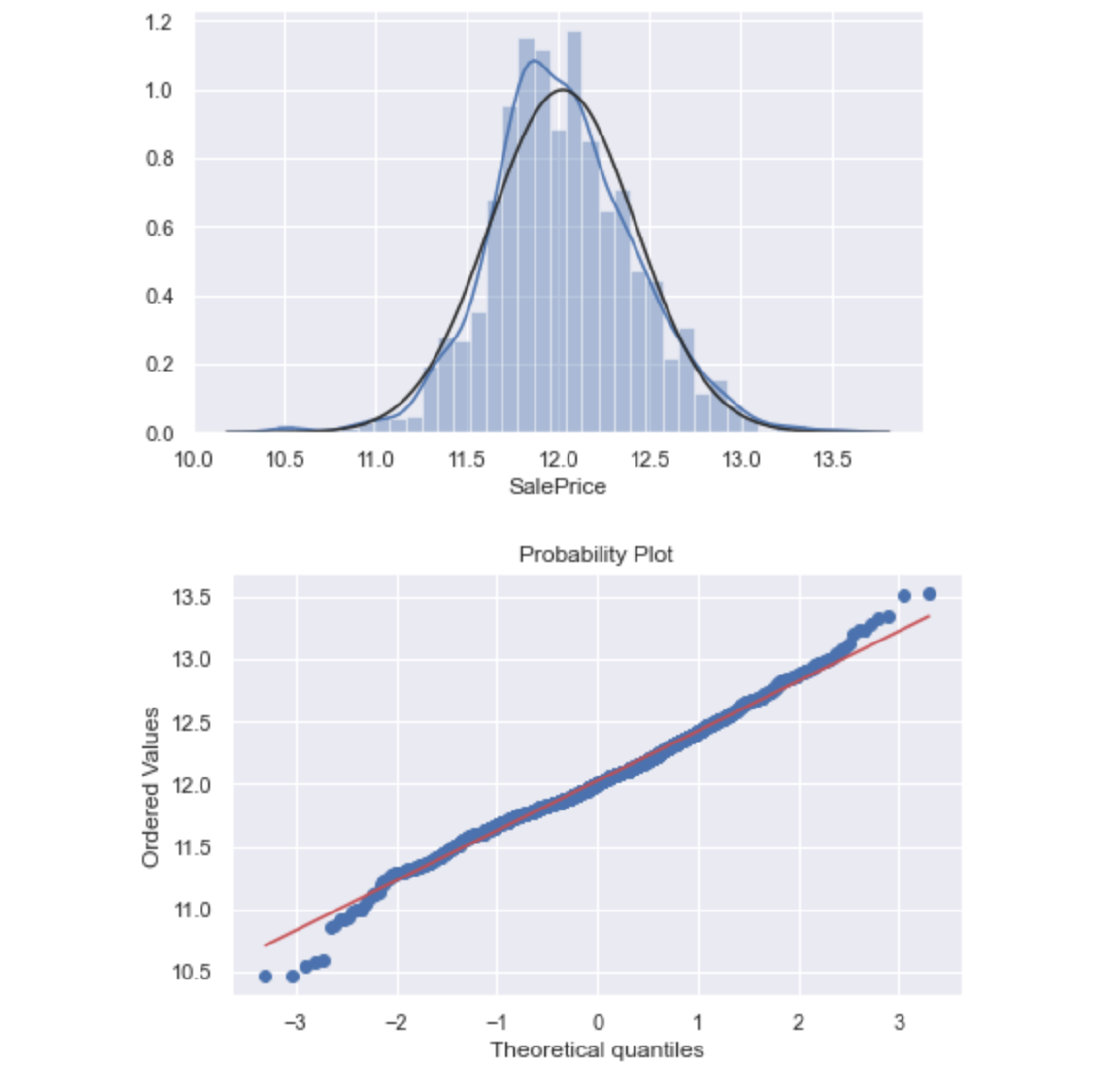
实施对数变换后效果好了很多的

Normality-归一化（GrLivArea）

sns.distplot(train["GrLivArea"],fit=norm)
fig = plt.figure()
res = stats.probplot(train["GrLivArea"], plot=plt)

对数变换前的效果：

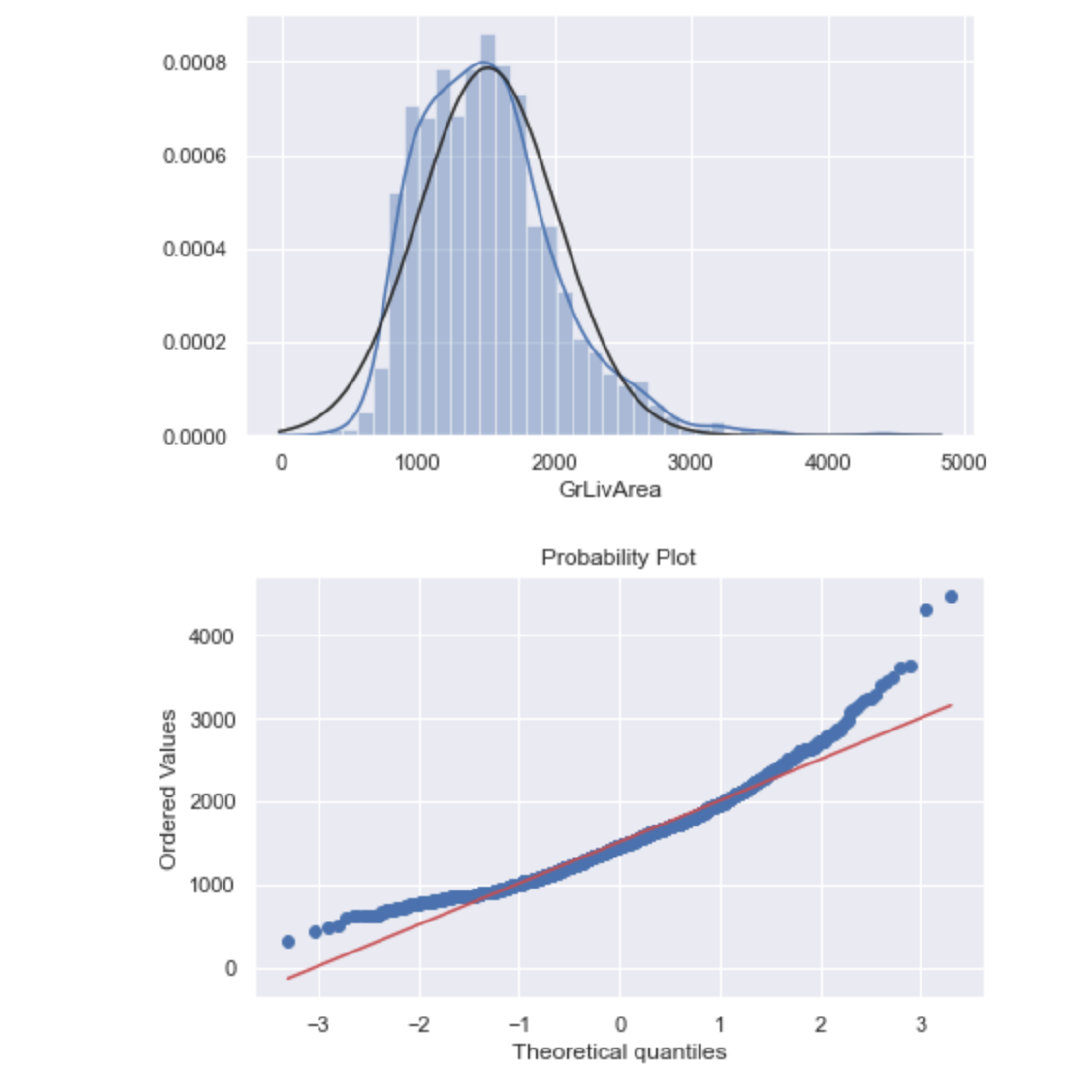
执行对数变换及效果：

# 执行相同的对数操作
train["GrLivArea"] = np.log(train["GrLivArea"])

sns.distplot(train["GrLivArea"],fit=norm)
fig = plt.figure()
res = stats.probplot(train["GrLivArea"], plot=plt)

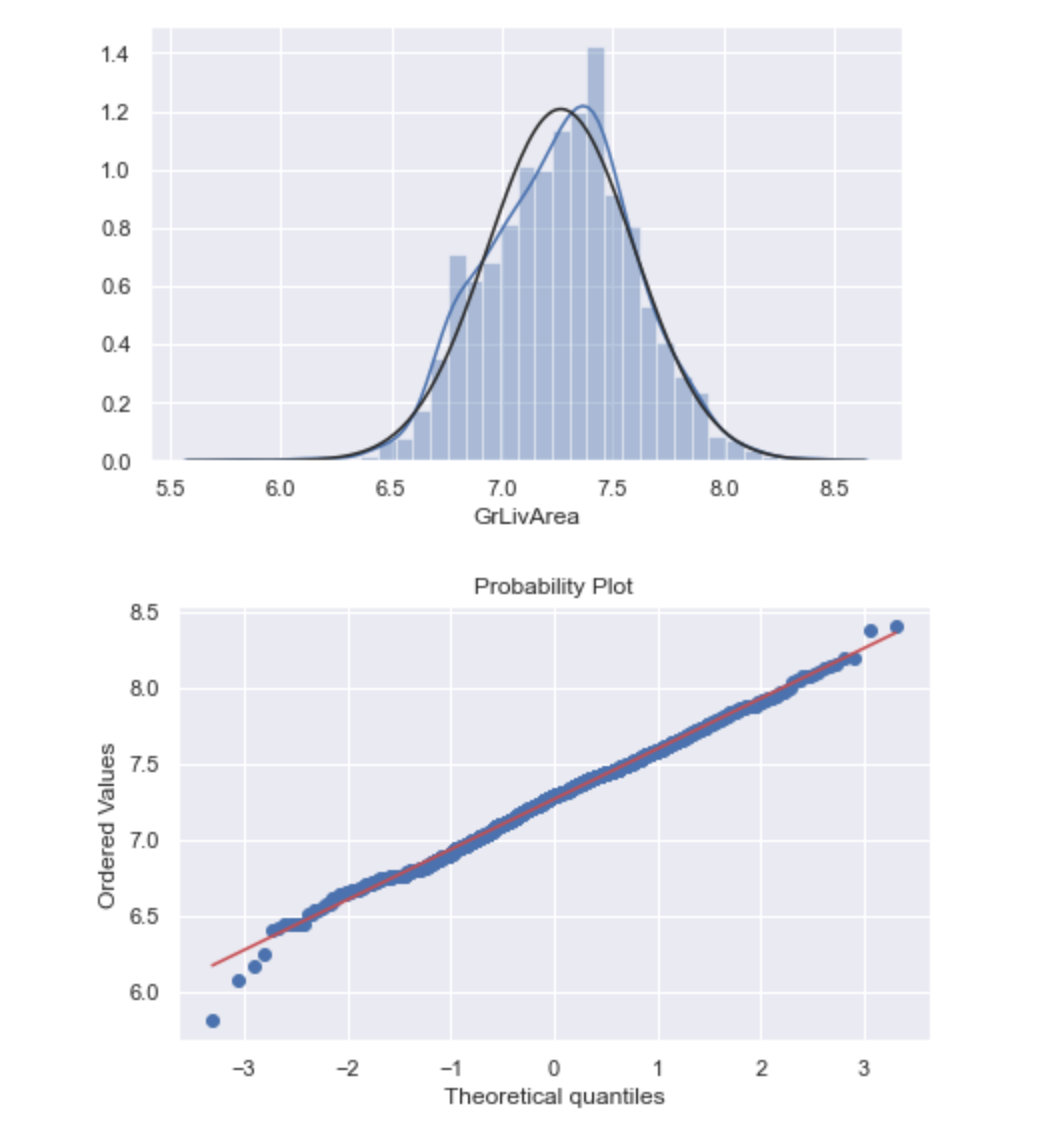
Normality-归一化（TotalBsmtSF）

sns.distplot(train["TotalBsmtSF"],fit=norm)
fig = plt.figure()
res = stats.probplot(train["TotalBsmtSF"], plot=plt)

处理之前的效果：

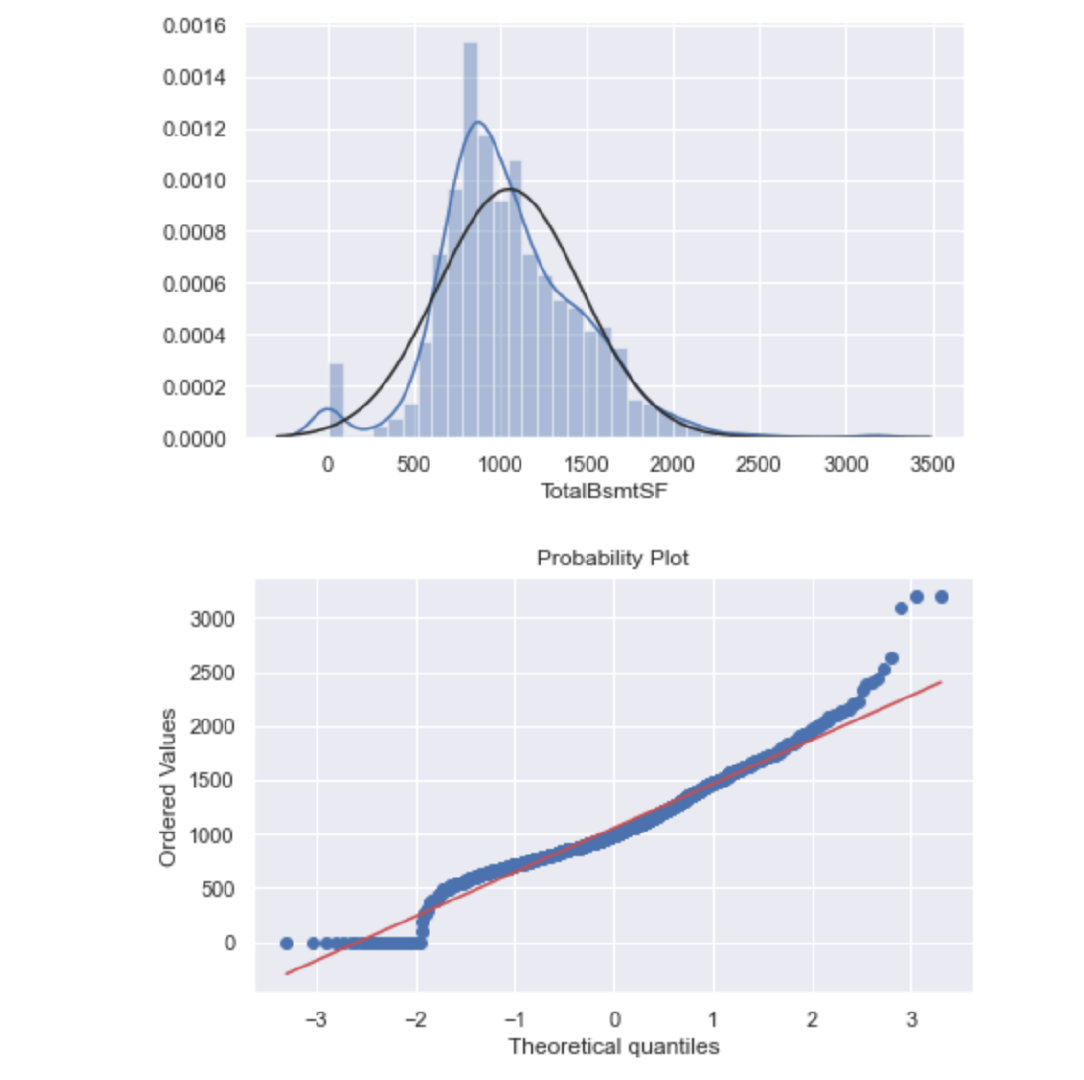
如何处理上面的特殊部分？

# 增加一列数据
train['HasBsmt'] = 0

# 当TotalBsmtSF>0 则赋值1
train.loc[train['TotalBsmtSF']>0,'HasBsmt'] = 1

# 对数转换：等于1的部分
train.loc[train['HasBsmt']==1,'TotalBsmtSF'] = np.log(train['TotalBsmtSF'])

# 绘图
data = train[train['TotalBsmtSF']>0]['TotalBsmtSF']
sns.distplot(data,fit=norm)
fig = plt.figure()
res = stats.probplot(data, plot=plt)

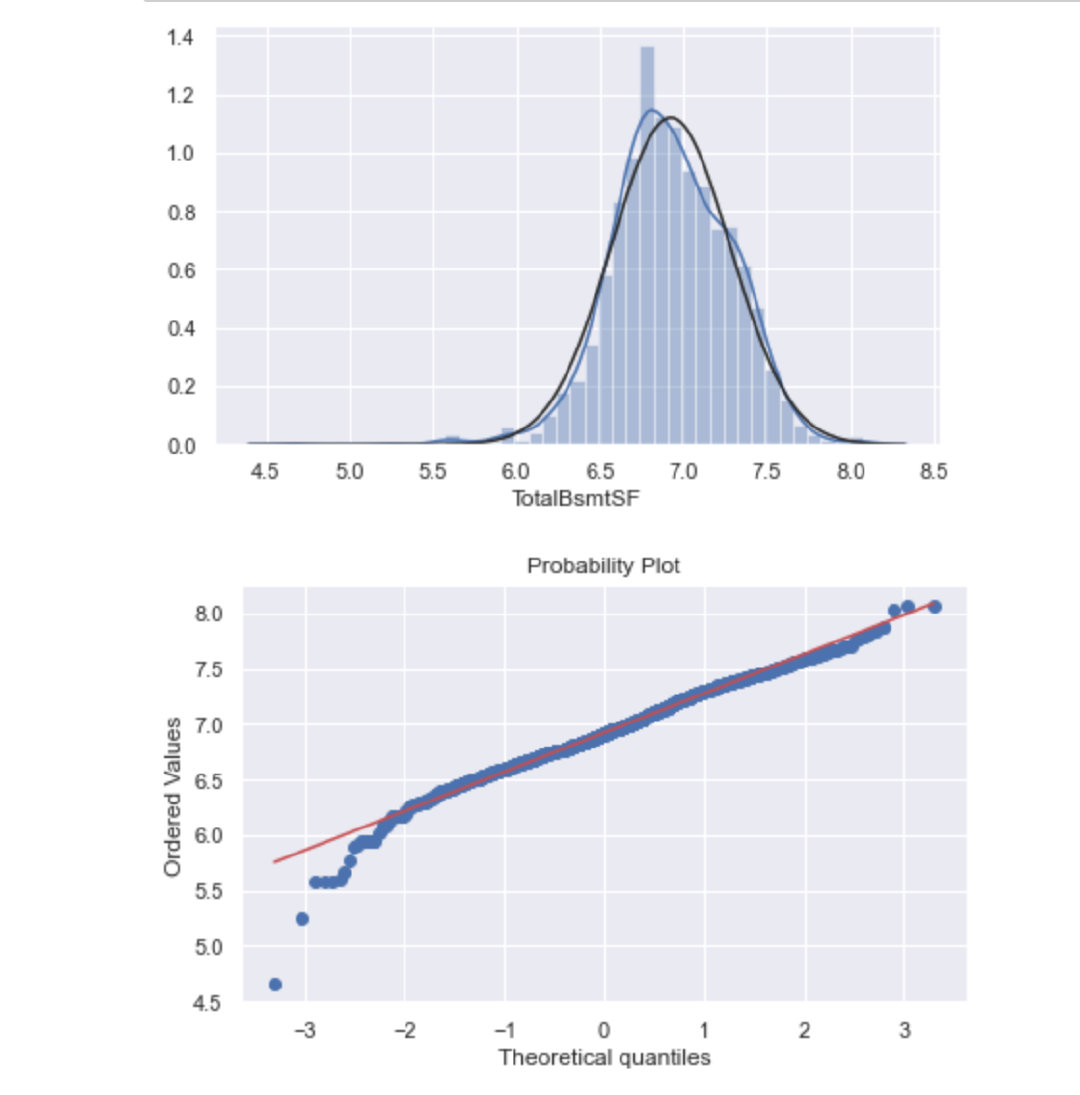
同方差性

检验两个变量之间的同方差性最好的方法就是作图。

The best approach to test homoscedasticity for two metric variables is graphically

1、讨论：‘SalePrice’ 和’GrLivArea’之间的关系

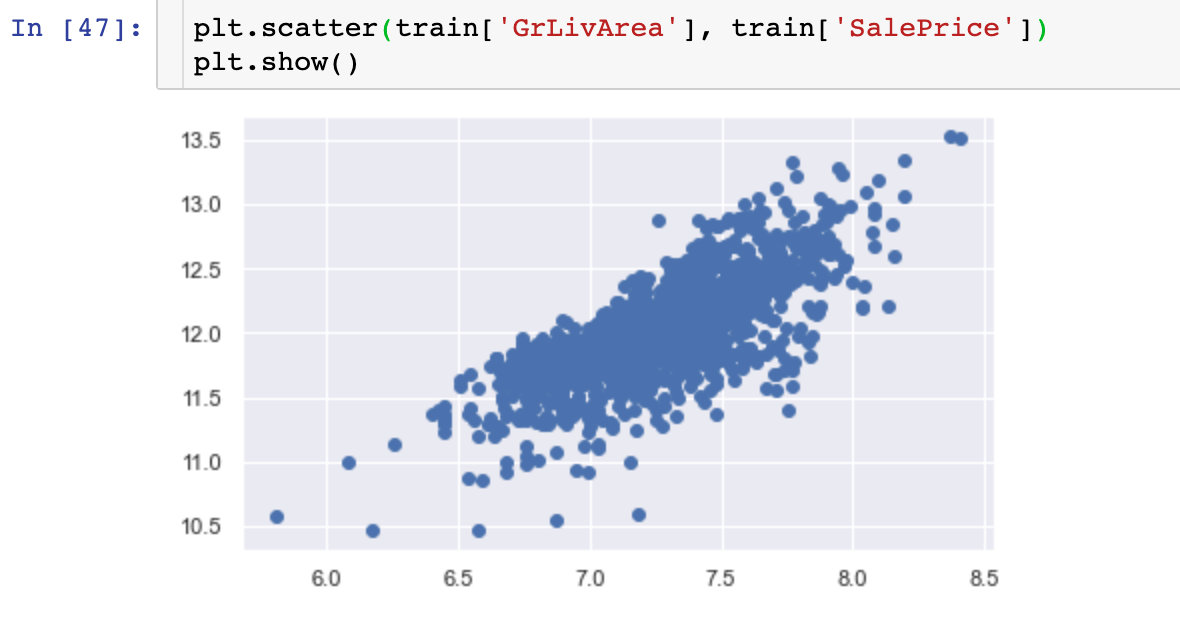
2、讨论SalePrice’ 和 ‘TotalBsmtSF’

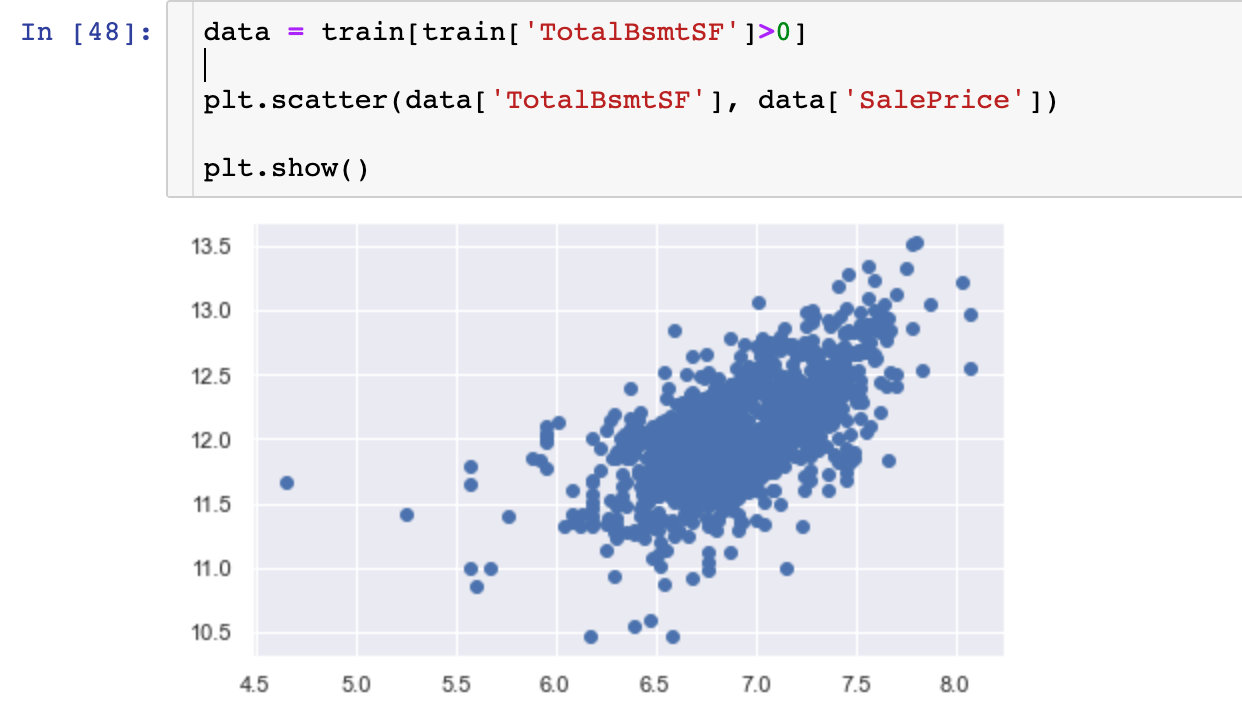
We can say that, in general, ‘SalePrice’ exhibit equal levels of variance across the range of ‘TotalBsmtSF’. Cool!

从上面的两张图中，我们看到：销售价格和另外两个变量都是呈现一定的正向关系

生成哑变量

虚拟变量( Dummy Variables) 又称虚设变量、名义变量或哑变量，用以反映质的属性的一个人工变量，是量化了的自变量，通常取值为0或1。

Pandas中的get_dummies函数能够实现：

train = pd.get_dummies(train)  # 生成哑变量
train

总结

至此，我们完成了以下的内容：

1. 整体变量间的相关性分析
2. 重点分析了变量“SalePrice”
3. 处理缺失值和异常值（离群点）
4. 做了一些统计分析，将分类变量变成了哑变量

自己需要后续补充深入学习的点：

• 多元统计分析
• 偏度和峰度
• 哑变量的深入
• 标准化和归一化

关于数据集的领取，公众号后台回复：房价。看完整篇文章的分析过程，有什么感受呢？