《数值分析》-- 拉格朗日插值
Posted 胜天半月子
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了《数值分析》-- 拉格朗日插值相关的知识,希望对你有一定的参考价值。
问题

一、拉格朗日插值基函数



- n=1时一次基函数
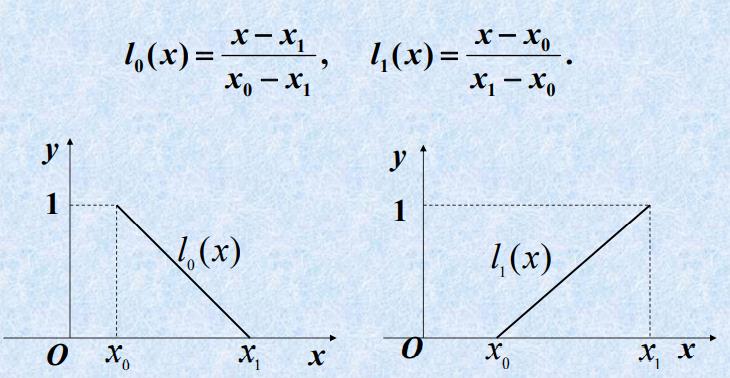
- 两点线性插值问题
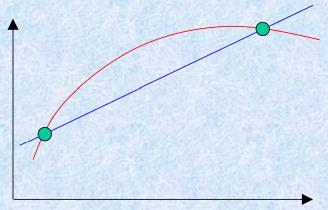
- 问题:即已知函数 f(x)在点 x 0 x_0 x0和 x 1 x_1 x1点的函数值
y 0 y_0 y0=f( x 0 x_0 x0), y 1 y_1 y1=f( x 1 x_1 x1).
求线性函数 L 1 L_1 L1(x)= a 0 a_0 a0+ a 1 a_1 a1x
使满足条件: L 1 L_1 L1( x 0 x_0 x0)= y 0 y_0 y0, L 1 L_1 L1( x 1 x_1 x1)= y 1 y_1 y1
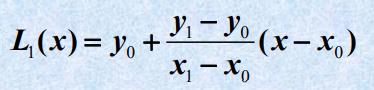
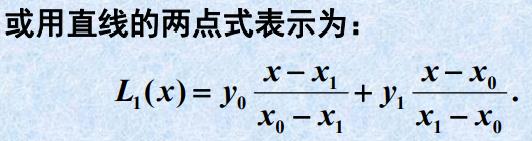
①:把x= x 0 x_0 x0带入 L 1 L_1 L1(x)中, L 1 ( x 0 ) L_1(x_0) L1(x0) = y 0 y_0 y0 + 0 = y 0 y_0 y0
②:把x= x 1 x_1 x1带入 L 1 L_1 L1(x)中, L 1 L_1 L1( x 1 x_1 x1) = y 0 y_0 y0 + ( y 1 y_1 y1- y 0 y_0 y0)( x 1 x_1 x1- x 0 x_0 x0) / ( x 1 x_1 x1- x 0 x_0 x0) = y 0 y_0 y0 + y 1 y_1 y1 - y 0 y_0 y0 = y 1 y_1 y1
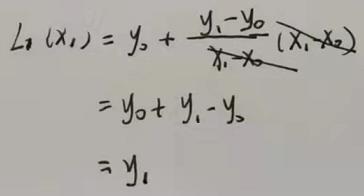
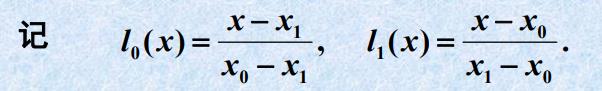
则称 l 0 l_0 l0(x)叫做点 x 0 x_0 x0的一次插值基函数, l 1 l_1 l1(x)叫
做点 x 1 x_1 x1的一次插值基函数

当x= x 0 x_0 x0时, l 0 l_0 l0=1; x= x 1 x_1 x1时, l 0 l_0 l0=0;
当x= x 0 x_0 x0时, l 1 l_1 l1=0; x= x 1 x_1 x1时, l 1 l_1 l1=1;
- n=2时二次基函数
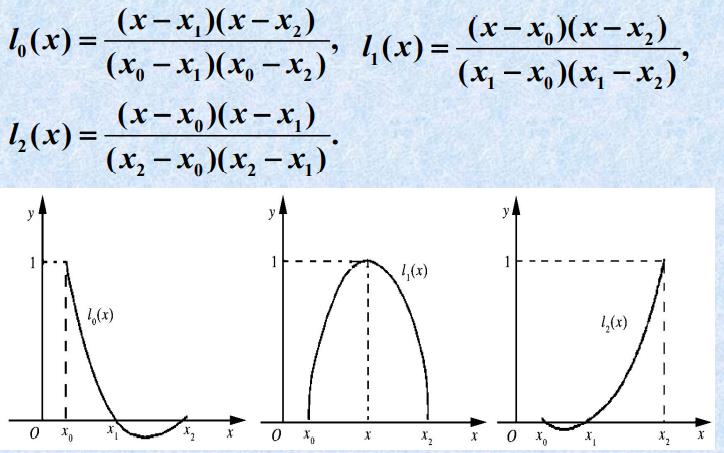
二、拉格朗日插值多项式

对上述举例:
begin---------------------------------------------
- n=1时
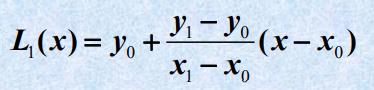
①:把x= x 0 x_0 x0带入 L 1 L_1 L1(x)中,
L1(x0)= y 0 y_0 y0 + 0 = y 0 y_0 y0
②:把x= x 1 x_1 x1带入 L 1 L_1 L1(x)中,L1(x1)= y 0 y_0 y0 + ( y 1 y_1 y1- y 0 y_0 y0)( x 1 x_1 x1- x 0 x_0 x0) / ( x 1 x_1 x1- x 0 x_0 x0) = y 0 y_0 y0 + y以上是关于《数值分析》-- 拉格朗日插值的主要内容,如果未能解决你的问题,请参考以下文章