节点：节点包括一个数据元素及若干指向其他子树的分支。
节点的度：节点所拥有子树的个数称为节点的度。
叶节点：度为0的节点成为叶结点，叶结点也称为终端节点。
分支节点：度不为0的节点称为分支节点，分支节点又称非终端节点。一棵树中排除叶结点外的所有节点都是分支节点。
祖先节点：从根节点到该节点所经分支上的所有节点。
子孙节点：以某节点为根节点的子树中所有节点
双亲节点：树中某节点有孩子节点，则这个节点称为它孩子节点的双亲节点，双亲节点也成为前驱节点。
孩子节点：树中一个节点的子树的根节点称为该节点的孩子节点，孩子节点也称为后继节点。
兄弟节点：具有相同双亲节点的节点称为兄弟节点。
树的度：树中所有节点的度的最大值成为该树的度。
节点的层次：从根节点到树中某节点所经路径上的分支也称为该节点的层次，根节点的层次为1，其他节点层次是双亲节点层次加1.
树的深度：树中所有节点的层次的最大值称为该树的深度。

1）考虑结点K。根A到结点K的唯一路径上的任意结点，称为结点K的祖先。如结点B是结点K的祖先，而结点K是结点B的子孙。路径上最接近结点K的结点K的结点E称为K的双亲，而K为结点E的孩子。根A是树中唯一没有双亲的结点。有相同双亲的结点称为兄弟，如结点K和结点L有相同的双亲E，即K和L为兄弟。

2）树中一个结点的孩子个数称为该结点的度，树中结点的最大度数称为树的度。如结点B的度等于2，结点D的度为3,树的度为3。

3）度大于0的结点称为分支结点(又称非终端结点);度为0 (没有子女结点)的结点称为叶子结点(又称终端结点)。在分支结点中，每个结点的分支数就是该结点的度。

4)结点的深度、高度和层次。结点的层次从树根开始定义，根结点为第1层，它的子结点为第2层，

以此类雅。双亲在阿一层的结点互为堂兄弟，图5.1 中结点G与E.EH.互为意兄弟。结点的深度是从根结点开始自顶向下连层累加的。结点的高度是从叶结点开始自底向上逐层累加的。树的高度(或深度)是树中结点的最大层数。

5)有序树和无序树。树中结点的各子树从左到右是有次序的，不能互换，称该树为有序树，否则称为无序树。假设图5.1为有序树，若将子结点位置互换，则变成一棵不同的树。

6)路径和路径长度。树中两个结点之间的路径是由这两个结点之间所经过的结点序列构成的，而路径长度是路径上所经过的边的个数。
注意:由于树中的分支是有向的，即从双亲指向孩子，所以树中的路径是从上向下的，同一双亲的两个孩子之间不存在路径。

7)森林。森林是m (m>=0)棵互不相交的树的集合。森林的概念与树的概念十分相近，因为只要把树的根结点删去就成了森林。反之，只要给m棵独立的树加上一个结点，并把这m棵树作为该结点的子树，则森林就变成了树。

三、树的性质

1)树中的结点数等于所有结点的度数加1.

2)度为m的树中第i层上至多有m^(i-1)个结点(i>=1)。

3)高度为h的m叉树至多有(m^h-1)/ (m - 1) 个结点”。

4)具有n个结点的m又树的最小高度为㏒m (n(m -1)+ 1)

四、什么是二叉树？

1、基本概念

二叉树，就是度不差过2的树（节点最多有两个分杈）

二又树是另一种树形结构，其特点是每个结点至多只有两棵子树 (即二叉树中不存在度大于2的结点)。并且二叉树的子树有左右之分，其次序不能任意顺倒。

2、二叉树的五种基本形态

1、空二叉树（什么都没有，nothing）

2、只有一个根节点的二叉树（左右子树为空）

3、右子树为空的二叉树（右腿断了）

4、左子树为空的二叉树（左腿断了）

5、左右子树都非空的的二叉树（既有左子树又有右子树）

3、二叉树的性质

性质1：二叉树第i层上的结点数目最多为2^（i-1）(i>=1)

性质2：深度为k的二叉树至多有2^k - 1个结点（k>=1）

性质3：包含n个结点的二叉树的高度至少为(log2n)+1

性质4：在任意一棵二叉树中，若终端结点的个数为n0，度为2的结点数为n2，则n0=n2+1

五、满二叉树、完全二叉树和二叉查找树

1、满二叉树

高度为h，并且由2h-1个结点组成的二叉树，称为满二叉树。

2、完全二叉树

一棵二叉树中，只有最下面两层结点的度可以小于2，并且最下层的叶结点集中在靠左的若干位置上，这样的二叉树称为完全二叉树。

特点：叶子结点只能出现在最下层和次下层，且最下层的叶子结点集中在树的左部。显然，一棵满二叉树必定是一棵完全二叉树，而完全二叉树未必是满二叉树。

例题：如果一个完全二叉树的结点总数为768个，求叶子结点的个数

由二叉树的性质知：n0=n2+1，将之带入768=n0+n1+n2中得：768=n1+2n2+1，因为完全二叉树度为1的结点个数要么为0，要么为1，那么就把n1=0或者1都代入公式中，很容易发现n1=1才符合条件。所以算出来n2=383，所以叶子结点个数n0=n2+1=384。

总结规律：如果一棵完全二叉树的结点总数为n，那么叶子结点等于n/2（当n为偶数时）或者(n+1)/2（当n为奇数时）

3、二叉查找树

二叉查找树又被称为二叉搜索树。设x为二叉查找树中的一个结点，x结点包含关键字key，结点x的key值计为key[x]。如果y是x的左子树中的一个结点，则key[y]<=key[x]；如果y是x的右子树的一个结点，则key[y]>=key[x]

（1）若任意结点的左子树不空，则左子树上所有结点的值均小于它的根结点的值。

（2）任意结点的右子树不空，则右子树上所有结点的值均大于它的根结点的值。

（3）任意结点的左、右子树也分别为二叉查找树。

（4）没有键值相等的结点。

六、二叉树的遍历

遵循某种次序，遍历二叉树中的所有节点，使得每个节点被访问一次，而且仅访问一次。“访问”：即对节点施行某些操作。

前（先）序遍历：先访问根节点，再访问左子树，最后访问右子树。
中序遍历：先访问左子树，再访问根节点，最后访问右子树。
后序遍历：先访问左子树，再访问右子树，最后访问根节点。

1、先序遍历

先序遍历：（1）访问根节点；（2）采用先序递归遍历左子树；（3）采用先序递归遍历右子树；

(注：每个节点的分支都遵循下述的访问顺序，体现“递归调用”)

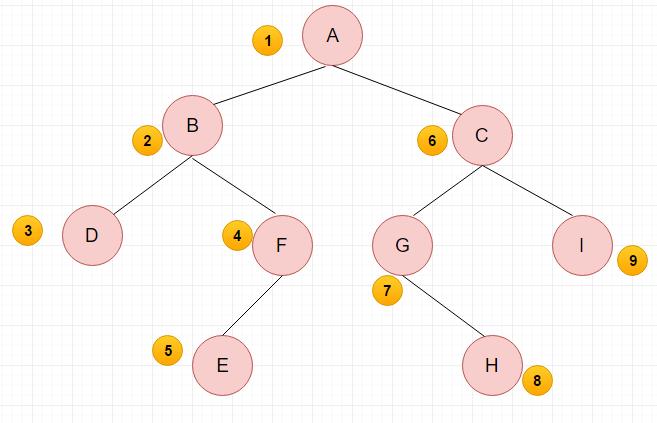
先序遍历结果：A BDFE CGHI

步骤：

（1）先访问根节点A，

（2）A分为左右两个子树，因为是递归调用，所以左子树也遵循“先根节点-再左-再右”的顺序，所以访问B节点，

（3）然后访问D节点，

（4）访问F节点的时候有分支，同样遵循“先根节点-再左--再右”的顺序,

(5)访问E节点，此时左边的大的子树已经访问完毕，

(6)然后遵循最后访问右子树的顺序，访问右边大的子树，右边大子树同样先访问根节点C,

(7)访问左子树G,

(8)因为G的左子树没有，所以接下俩访问G的右子树H,

(9)最后访问C的右子树I

2、中序遍历

中序遍历：（1）采用中序遍历左子树；（2）访问根节点；（3）采用中序遍历右子树

中序遍历结果：DBEF A GHCI

3、后序遍历

后序遍历：（1）采用后序递归遍历左子树；（2）采用后序递归遍历右子树；（3）访问根节点；

后序遍历的结果：DEFB HGIC A

七、君子藏器于身，待时而动

《周易·系辞传下·第五章》

《易》曰「憧憧往来，朋从尔思。」子曰：「天下何思何虑？天下同归而殊途，一致而百虑。天下何思何虑？日往则月来，月往则日来，日月相推而明生焉。寒往则暑来，暑往则寒来，寒暑相推而岁成焉。往者屈也，来者信也，屈信相感而利生焉。尺蠖之屈，以求信也；龙蛇之蛰，以存身也。精义入神，以致用也；利用安身，以崇德也。过此以往，未之或知也；穷神知化，德之盛也。」
　　《易》曰：「困于石，据于蒺藜，入于其宫，不见其妻，凶。」子曰：「非所困而困焉，名必辱。非所据而据焉，身必危。既辱且危，死期将至，妻其可得见耶！」
　　《易》曰：「公用射隼于高墉之上，获之，无不利。」子曰：「隼者，禽也；弓矢者，器也；射之者，人也。君子藏器于身，待时而动，何不利之有？动而不括，是以出而有获，语成器而动者也。」
　　子曰：「小人不耻不仁，不畏不义，不见利不劝，不威不惩。小惩而大诫，此小人之福也。《易》曰：『履校灭趾，无咎。』此之谓也。」
　　「善不积不足以成名，恶不积不足以灭身。小人以小善为无益而弗为也，以小恶为无伤而弗去也，故恶积而不可掩，罪大而不可解。《易》曰：『何校灭耳，凶。』」
　　子曰：「危者，安其位者也；亡者，保其存者也；乱者，有其治者也。是故君子安而不忘危，存而不忘亡，治而不忘乱，是以身安而国家可保也。《易》曰：『其亡其亡，系于苞桑。』」
　　子曰：「德薄而位尊，知小而谋大，力少而任重，鲜不及矣。《易》曰：『鼎折足，覆公餗，其形渥，凶。』言不胜其任也。」
　　子曰：「知几其神乎！君子上交不谄，下交不渎，其知几乎？几者，动之微，吉之先见者也。君子见几而作，不俟终日。
　　《易》曰：『介于石，不终日，贞吉。』介如石焉，宁用终日？断可识矣。君子知微知彰，知柔知刚，万夫之望。」子曰：「颜氏之子，其殆庶几乎？有不善未尝不知，知之未尝复行也。《易》曰：『不远复，无祗悔，元吉。』」
　　天地氤氲，万物化醇。男女构精，万物化生。《易》曰：『三人行则损一人，一人行则得其友。』言致一也。
　　子曰：「君子安其身而后动，易其心而后语，定其交而后求。君子修此三者，故全也。危以动，则民不与也；惧以语，则民不应也；无交而求，则民不与也；莫之与，则伤之者至矣。《易》曰：『莫益之，或击之，立心勿恒，凶。』」

以上是关于数据结构_树与二叉树的主要内容，如果未能解决你的问题，请参考以下文章

(王道408考研数据结构)第五章树-第三节4：树与二叉树的转换