2021年人工神经网络第三次作业-第二题:遗传算法与人工神经网络-参考答案
Posted 卓晴
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2021年人工神经网络第三次作业-第二题:遗传算法与人工神经网络-参考答案相关的知识,希望对你有一定的参考价值。

简 介: 给出了对于BP网络求解异或问题过程中,利用遗传算法完成网络演变的过程。所使用的遗传算法是最基本的遗传算法。利用遗传算法对于网络的系数进行演变,可以对网络系数初始化过程进行优化。对于不同的遗传算法参数对于结果的影响进行的试验对比。
关键词: 遗传算法,NN,人工神经网络
§02 第二题:
遗传算法与NN
遗传算法与NN
一、作业要求
利用遗传算法可以训练神经网络的权系数。特别是神经网络用于复杂对象控制的情况下,无法给出神经网络准确的期望输出,只能给出整个系统性能的评价时,可以使用遗传算法完成网络训练。
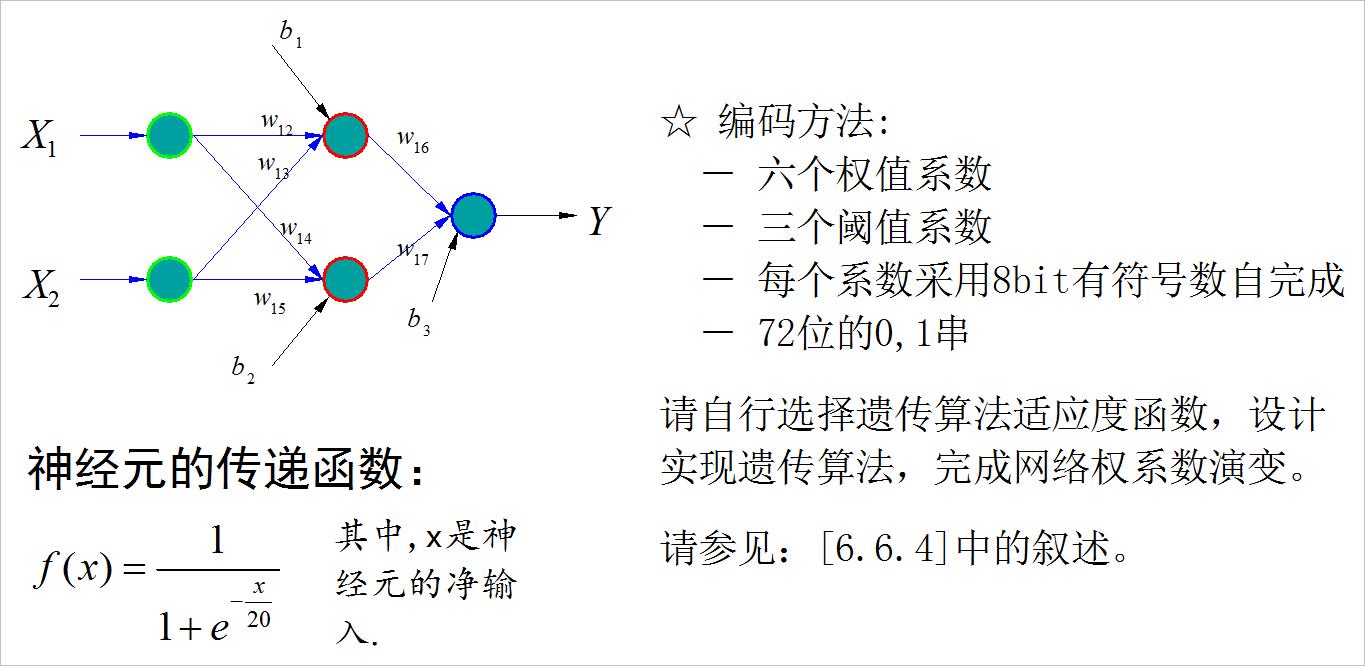
▲ 图1.1.1 异或网络以及传递函数要求
二、作业求解
1、异或问题
根据题目中给定的神经元传递函数,它的输出在(0,1)之间,使用(-1,1)来表示异或问题中样本的输出,(0,1)表示样本的期望输出。对应的四个样本如下表格所示:
| 样本 | 输入(X1,X2) | 输出:Y |
|---|---|---|
| 样本1 | 1,1 | 0 |
| 样本2 | -1,1 | 1 |
| 样本3 | 1,-1 | 1 |
| 样本4 | -1,-1 | 0 |
2、构造遗传算法
(1)网络个体使用72bit 0-1 串表示
对题目中的神经网络,存在着六个权系数 w 1 , w 2 , ⋯ , w 6 w_1 ,w_2 , \\cdots ,w_6 w1,w2,⋯,w6和三个阈值 b 1 , b 2 , b 3 b_1 ,b_2 ,b_3 b1,b2,b3。使用8bit的有符号整数表示。这样九个参数共由72bit表示。
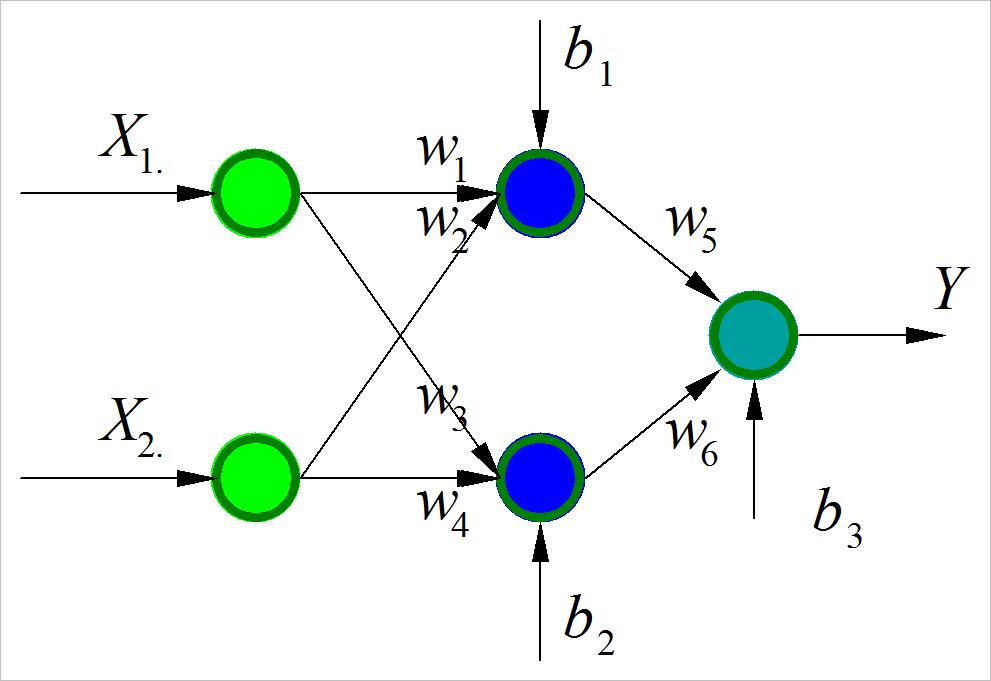
▲ 图1.2.1 求解异或问题的神经网络
72bit分配关系如下:

▲ 图1.2.2 72bit 0-1串与网络系数之间关系
前48bit分别对应 w 1 , 2 , ⋯ , 6 w_1,2, \\cdots ,6 w1,2,⋯,6,后面24bit对于 b 1 , b 2 , b 3 b_1 ,b_2 ,b_3 b1,b2,b3。每8bit分别表示 -128 ~ 127 之间的整数。
(2)个体适应度
对于任一个72bit 0-1串,根据上述编码,将其转换成网络的权系数以及偏移量。
比如,对于一个72位的 0 - 1串,
[1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0]
转换成对应九个有符号整形数字,分别对应 w 1 , 2 , ⋯ , 6 w_1,2, \\cdots ,6 w1,2,⋯,6以及 b 1 , 2 , 3 b_1,2,3 b1,2,3。
[-120, -96, -13, -10, 37, -48, -66, -5, -14]
将72bit 0-1 字符串转换成9个参数的程序如下:
def bit8(r):
bytestr = ''.join(['%d'%rr for rr in r])
n = int(bytestr, 2)
if n >= 128: n = n - 256
return n
def wb012(wb):
wwbb = list(zip(*([iter(wb)]*8)))
wb = [bit8(r) for r in wwbb]
return wb
将上述参数代入网络【1.2.1】中,根据神经元的传递函数:
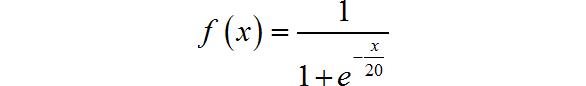
可以计算出表格【2-2-1】中四个样本对应的网络输出。
[0.2359961611001143, 0.16208119759951686, 0.16270729983112092, 0.16270729983112092]
定义,个体适应度为:
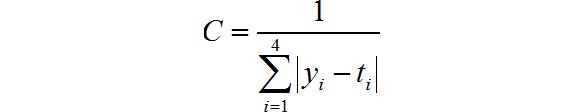
其中, y i , t i , i = 1 , 2 , 3 , 4 y_i ,t_i ,i = 1,2,3,4 yi,ti,i=1,2,3,4分别是四个样本的网络输出以及期望值。
具体计算样本的适应度的函数为:
def fnn(x):
return 1/(1+exp(-x/20))
def xornn(wb, x1, x2):
v1 = fnn(x1*wb[0] + x2*wb[1] + wb[6])
v2 = fnn(x1*wb[2] + x2*wb[3] + wb[7])
y = fnn(v1*wb[4] + v2*wb[5] + wb[8])
return y
#------------------------------------------------------------
x12 = ((1,1),(1,-1),(-1,1),(-1,1))
yt = (0,1,1,0)
def xornnout(wb):
global x12
return [xornn(wb,a[0],a[1]) for a in x12]
def xorerr(yo):
global yt
error = sum([abs(x-y) for x,y in zip(yt,yo)])
return error
def funcC(error):
if error == 0: return 100000
else: return 1/e
(3)构建选择,变异,交叉算子
Ⅰ.选择算子
定义遗传算法选择比率:GA_SELECT_RATIO,从给定的样本中选择适应度在前比率的样本,遗传到下一代。
def GA_select(a, num=0):
if num == 0:
num = len(a)
ac =