主成分分析（PCA）原理

Posted 2023-03-11 吃肉的小馒头

主成分分析（PCA）原理

---

在高维数据处理中，为了简化计算量以及储存空间，需要对这些高维数据进行一定程度上的降维，并尽量保证数据的不失真。PCA和ICA是两种常用的降维方法。

PCA：principal component analysis ，主成分分析

ICA ：Independent component analysis，独立成分分析

PCA,ICA都是统计理论当中的概念，在机器学习当中应用很广，比如图像，语音，通信的分析处理。

从线性代数的角度去理解，PCA和ICA都是要找到一组基，这组基张成一个特征空间，数据的处理就都需要映射到新空间中去。

两者常用于机器学习中提取特征后的降维操作。

PCA是找出信号当中的不相关部分(正交性），对应二阶统计量分析。PCA的实现一般有两种，一种是用特征值分解去实现的，一种是用奇异值(SVD)分解去实现。特征值分解也有很多的局限，比如说变换的矩阵必须是方阵,SVD没有这个限制。

PCA的问题其实是一个基的变换，使得变换后的数据有着最大的方差。方差的大小描述的是一个变量的信息量，我们在讲一个东西的稳定性的时候，往往说要减小方差，如果一个模型的方差很大，那就说明模型不稳定了。但是对于我们用于机器学习的数据（主要是训练数据），方差大才有意义，不然输入的数据都是同一个点，那方差就为0了，这样输入的多个数据就等同于一个数据了。

主成分分析（Principal components analysis，以下简称PCA）是最重要的降维方法之一。在数据压缩消除冗余和数据噪音消除等领域都有广泛的应用。一般我们提到降维最容易想到的算法就是PCA，下面我们就对PCA的原理做一个总结。

1. PCA的思想

PCA顾名思义，就是找出数据里最主要的方面，用数据里最主要的方面来代替原始数据。具体的，假如我们的数据集是n维的，共有m个数据$(x^{(1)},x^{(2)},...,x^{(m)})$。我们希望将这m个数据的维度从n维降到n’维，希望这m个n’维的数据集尽可能的代表原始数据集。我们知道数据从n维降到n’维肯定会有损失，但是我们希望损失尽可能的小。那么如何让这n’维的数据尽可能表示原来的数据呢？

我们先看看最简单的情况，也就是n=2，n’=1,也就是将数据从二维降维到一维。数据如下图。我们希望找到某一个维度方向，它可以代表这两个维度的数据。图中列了两个向量方向，$u_1$和$u_2$，那么哪个向量可以更好的代表原始数据集呢？从直观上也可以看出，$u_1$比$u_2$好。

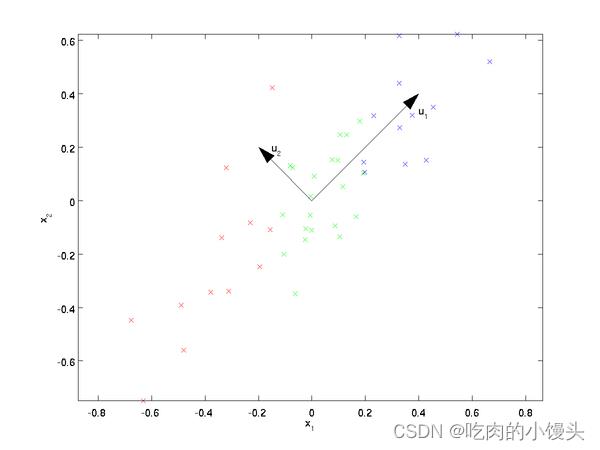
为什么$u_1$比$u_2$好呢？可以有两种解释，第一种解释是样本点到这个直线的距离足够近，第二种解释是样本点在这个直线上的投影能尽可能的分开。

假如我们把n’从1维推广到任意维，则我们的希望降维的标准为：样本点到这个超平面的距离足够近,或者说样本点在这个超平面上的投影能尽可能的分开。

基于上面的两种标准，我们可以得到PCA的两种等价推导。

2. PCA的推导:基于小于投影距离

我们首先看第一种解释的推导，即样本点到这个超平面的距离足够近。

假设m个n维数据$$(x^{(1)},x^{(2)},...,x^{(m)})$$都已经进行了标准化，即$\sum _{i=1}^m{x}^{(i)}=0$。经过投影变换后得到的新坐标系为$$w_1,w_2,...,w_n$$,其中w是标准正交基，即$||w|{|}_2=1,w_i^T{w}_j=0$。

如果我们将数据从n维降到n’维，即丢弃新坐标系中的部分坐标，则新的坐标系为$w_1,w_2,...,w_{n^{\prime }}$,样本点$x^{(i)}$在n’维坐标系中的投影为：$$z^{(i)}=(z_1^{(i)},z_2^{(i)},...,z_{n^{\prime }}^{(i)})$$.其中，$$z_j^{(i)}=w_j^T{x}^{(i)}$$是$x^{(i)}$在低维坐标系里第j维的坐标。

如果我们用$z^{(i)}$来恢复原始数据$x^{(i)}$,则得到的恢复数据$${\overline{x}}^{(i)}=\sum _{j=1}^{n^{\prime }}{z}_j^{(i)}{w}_j=W{z}^{(i)}$$,其中，W为标准正交基组成的矩阵。

现在我们考虑整个样本集，我们希望所有的样本到这个超平面的距离足够近，即最小化下式：$$\sum _{i=1}^m||{\overline{x}}^{(i)}-x^{(i)}|{|}_2^2$$

将这个式子进行整理，可以得到:

∑ i = 1 m ∣ ∣ x ‾ ( i ) − x ( i ) ∣ ∣ 2 2 = ∑ i = 1 m ∣ ∣ W z ( i ) − x ( i ) ∣ ∣ 2 2 = ∑ i = 1 m ( W z ( i ) ) T ( W z ( i ) ) − 2 ∑ i = 1 m ( W z ( i ) ) T x ( i ) + ∑ i = 1 m x ( i ) T x ( i ) = ∑ i = 1 m z ( i ) T z ( i ) − 2 ∑ i = 1 m z ( i ) T W T x ( i ) + ∑ i = 1 m x ( i ) T x ( i ) = ∑ i = 1 m z ( i ) T z ( i ) − 2 ∑ i = 1 m z ( i ) T z ( i ) + ∑ i = 1 m x ( i ) T x ( i ) = − ∑ i