学习数据结构笔记(14) --- [图]
Posted 小智RE0
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了学习数据结构笔记(14) --- [图]相关的知识，希望对你有一定的参考价值。
B站学习传送门–>尚硅谷Java数据结构与java算法（Java数据结构与算法）
文章目录
1.图的概述
图也是一种数据结构,这个在离散数学以及运筹学原理与应用这两门数学课程中有学习过
结点(顶点) 之间的连接线就是边;顶点附近可以有0个或者多个相邻顶点;
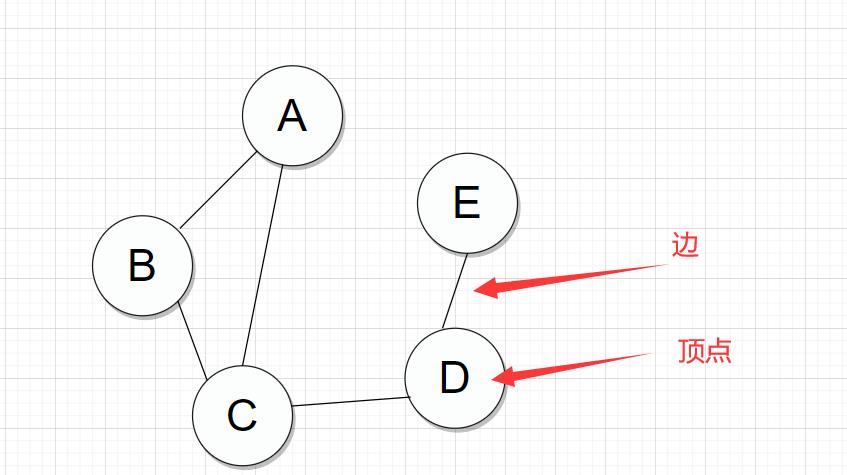
(1)无向图
无向图:顶点之间没有指定箭头方向的图;
路径:从一个顶点到另一个顶点之间经历的过程;
例如下图即使个无向图; A顶点和B顶点之间可以说是 A -> B,也可以说是B -> A.
比如说要算顶点A到顶点E的路径;
有两种方式: A -> B -> C -> D -> E
或者是: A -> C -> D -> E
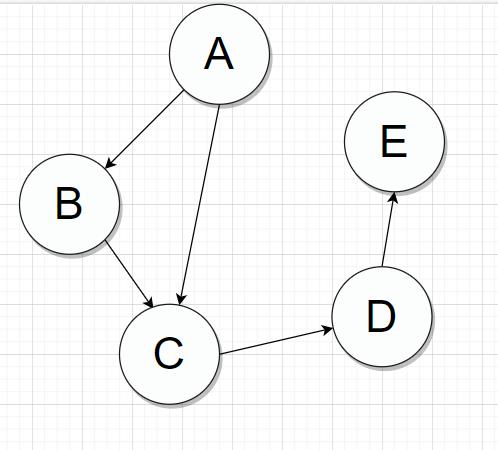
(2)有向图
像这样,为节点之间的路径加上指向,即有向图;
这样的话,A到B只能是 A->B
(3)带权图
为边赋予权值,即带权图,可分为无向带权图,有向带权图;
带权图也可称为网
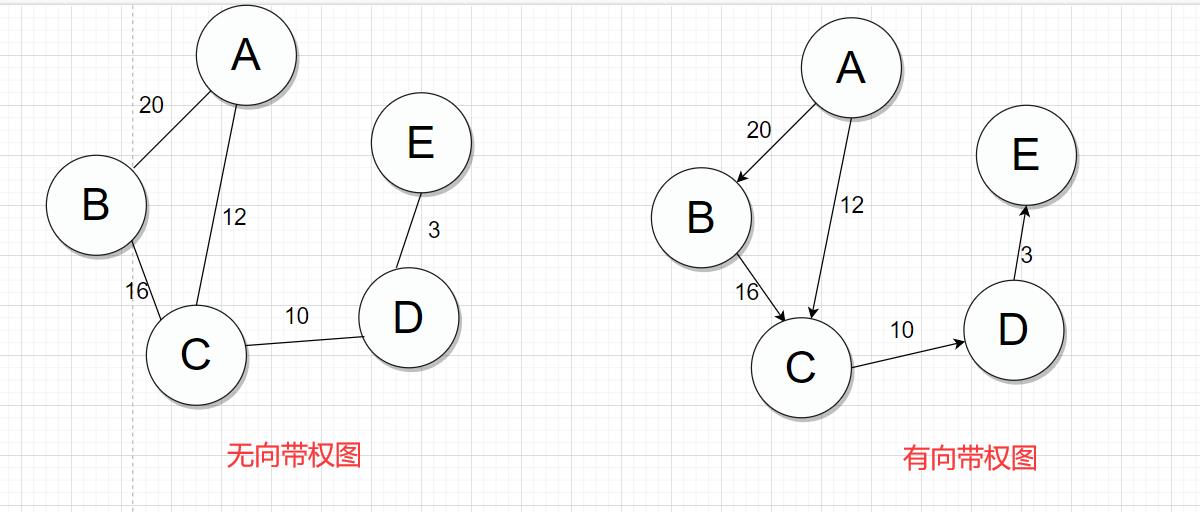
(4) 图的表示方式
图的表达方式可分为两种;
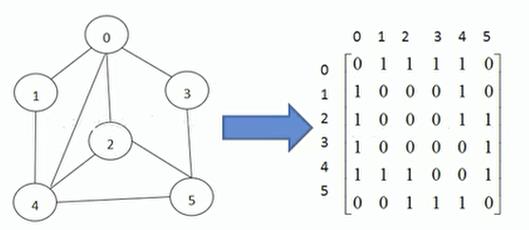
1.二维数组(邻接矩阵)
百度百科—>邻接矩阵
邻接矩阵（Adjacency Matrix）是表示顶点之间相邻关系的矩阵。设G=(V,E)是一个图，其中
V=v1,v2,…,vn。G的邻接矩阵是一个具有下列性质的n阶方阵：
①对无向图而言，邻接矩阵一定是对称的，而且主对角线一定为零（在此仅讨论无向简单图），副对角线不一定为0，有向图则不一定如此。
②在无向图中，任一顶点i的度为第i列（或第i行）所有非零元素的个数，在有向图中顶点i的出度为第i行所有非零元素的个数，而入度为第i列所有非零元素的个数。
③用邻接矩阵法表示图共需要n^2个空间，由于无向图的邻接矩阵一定具有对称关系，所以扣除对角线为零外，仅需要存储上三角形或下三角形的数据即可，因此仅需要n（n-1）/2个空间。
图例:
试着解读一下这个矩阵;
0->0无连接;[0,0] -->0
0->1之间仅连接了一条边;[0,1] -->1
0->2之间仅连接了一条边;[0,2] -->1
0->3之间仅连接了一条边;[0,3] -->1
0->4之间仅连接了一条边;[0,4] -->1
0->5之间无连接;[0,5] -->1
1到0之间连接了一条边;[1,0] -->1
1到1之间无连接;[1,1] -->0
1到2之间无连接[1,2] -->0
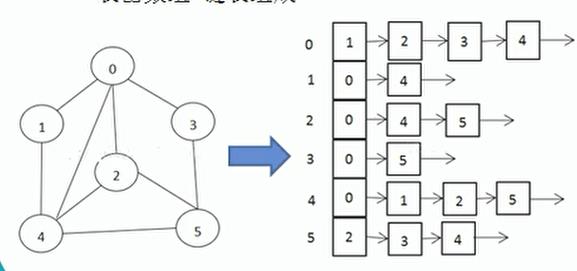
2.链表(邻接表)
百度百科—>邻接表
邻接表是图的一种最主要存储结构,用来描述图上的每一个点。对图的每个顶点建立一个容器（n个顶点建立n个容器），第i个容器中的结点包含顶点Vi的所有邻接顶点。实际上我们常用的邻接矩阵就是一种未离散化每个点的边集的邻接表。
在有向图中，描述每个点向别的节点连的边（点a->点b这种情况）。
在无向图中，描述每个点所有的边(点a-点b这种情况)
与邻接表相对应的存图方式叫做边集表，这种方法用一个容器存储所有的边;
图例:
这个结构的话就是数组加链表的形式进行存储;
这个邻接表它不会存储没有边的数据;仅存放有边的顶点数据;
2. 用代码实现无向带权图的创建
这次的话,就按这个无向图来创建一个图;并且用邻接矩阵来表示这个无向带权图
public class Graphs
//定义存储顶点;
private List<String> nodeList;
//邻接矩阵;
private int[][] matrixArray;
//边的个数;
private int sideNum;
/**
* 初始化图
* @param n 顶点的数量
*/
public Graphs(int n)
this.nodeList = new ArrayList<>(n);
this.matrixArray = new int[n][n];
this.sideNum = 0;
/**
* 添加新的顶点到集合中;
* @param node 添加的新顶点;
*/
public void addNode(String node)
this.nodeList.add(node);
/**
* 向邻接矩阵填入顶点之间的边 的权值
* @param v1 第一个顶点 (由0开始)
* @param v2 第二个顶点
* @param weight 边的权值
*/
public void addToArray(int v1 ,int v2 ,int weight)
//由于是无向图,所以两个方向都要标注;
this.matrixArray[v1][v2] = weight;
this.matrixArray[v2][v1] = weight;
//边的数量增加;
this.sideNum++;
/**
* 获取图中顶点的数量;
* @return 顶点数量
*/
public int getNodeNums()
return this.nodeList.size();
/**
* 获取图中边的数量;
* @return 边的数量
*/
public int getSideNum()
return this.sideNum;
/**
* 获取指定的顶点
* @param index 该节点在集合中的索引
* @return 指定顶点
*/
public String getNodeInfo(int index)
return this.nodeList.get(index);
/**
* 用邻接矩阵表示这张图
*/
public void describeGraphs()
for (int[] arr : matrixArray)
System.out.println(Arrays.toString(arr));
测试查看
public static void main(String[] args)
//测试;
Graphs graphs = new Graphs(5);
String[] nodeArr = "A市区","B市区","C市区","D市区","E市区";
Collections.addAll(graphs.nodeList, nodeArr);
System.out.println("当前图中的节点数量"+graphs.getNodeNums());
System.out.println("查看B市区-->"+graphs.getNodeInfo(1));
//手动添加边; [A-B,20] [A-C,12] [B-C,16] [C-D,10][D-E,3]
graphs.addToArray(0,1,20);
graphs.addToArray(0,2,12);
graphs.addToArray(1,2,16);
graphs.addToArray(2,3,10);
graphs.addToArray(3,4,3);
System.out.println("------图的结构------");
graphs.describeGraphs();
测试结果
当前图中的节点数量5
查看B市区-->B市区
------图的结构------
[0, 20, 12, 0, 0]
[20, 0, 16, 0, 0]
[12, 16, 0, 10, 0]
[0, 0, 10, 0, 3]
[0, 0, 0, 3, 0]
3.对图进行深度优先搜索(DFS)
在遍历访问时,首先访问的是当前顶点的第一个邻接顶点;重复操作;
这时一个递归的过程;
(1)首先从当前顶点
node1出发,并且进行标记;
(2)访问这个顶点的下一个邻接顶点node2;且进行标记;
(3)若找不到顶点node2,则回到第一步,从node1再次出发;找node1的另一个邻接顶点;
(4)若找到这顶点node2;并且这个顶点没有被访问过;那就对这个顶点进行操作,重复前面的步骤;
(5)找顶点node2的下一个邻接顶点
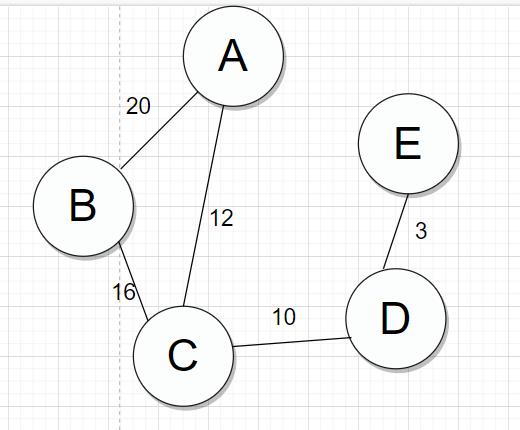
就用这个案例来看,
(1)我先拿到顶点A;把顶点A标记为已经访问;往后走A-B 以及A-C都拿到了;直到-1的情况;
(2)然后我去看顶点B,把顶点B标记为已访问;由于这是无向图;这时会走B - A;发现顶点A已经访问了,这时回到顶点B;去走B - C,再往后走发现已经-1了,停止;
(3)然后找到顶点C,标记顶点C为已经访问;顶点C这时首先会去走 C-A;发现顶点A已经访问,跳过,这时回到顶点C,去走 C- D ;再往后就到-1了;停止;
(4)然后找到顶点D;标记顶点D为已经访问,顶点D这时会先走D-C,发现顶点C已经访问,跳过,这时回到顶点D,会走D-E,再往后就没路了,停止;
(5)这时找到顶点E,标记顶点E为已经访问,顶点E会先找E-D,发现顶点D已经访问,则回到顶点E,没有路径了,结束;
A B C D E
A [0, 20, 12, 0, 0]
B [20, 0, 16, 0, 0]
C [12, 16, 0, 10, 0]
D [0, 0, 10, 0, 3]
E [0, 0, 0, 3, 0]
4.进行广度优先搜索(BFS)
需要借助队列作为辅助结构;
(1)访问到当前顶点node;标记为已访问;
(2)将当前顶点node存入队列,
(3)当队列非空,就继续操作
(4)队头顶点出队pollNode;
(5)查找当前节点pollNode的下一个邻接结点nextNode;
(6)若这个nextNode不存在;回到步骤(3),
(7)找到后,若这个nextNode没有被访问过;那就进行标记为已访问;
(8)nextNode入队;
(9)找这个nextNode的下一个邻接顶点;到步骤(6)
这个案例;
首先顶点A入队,标记为已经访问;
这时顶点A出队,判断到顶点A后还有邻接顶点B,将顶点B标记为已访问,然后没停止,这时还去找B的邻接顶点C,将顶点C标记为已访问;再往后,发现找不到C的邻接顶点了;
这时顶点B出队;判断到B-A,但是A已经被访问了,跳过;这时再走到B-C注意到C已经被访问了;跳过,五路可走了;
这时顶点C出队,判断到C-A, C-B,这时A和B都已经被访问了;跳过,这时可以走到C-D,将D标记为已访问;再往后无路可走;
这时让顶点D出队,判断到D-C,这时C已经被访问了,跳过;发现可走到D-E,将E标记为已访问;结束
可能这个案例不太好,所以相比于深度优先搜索,没看出效率的简化;
A B C D E
A [0, 20, 12, 0, 0]
B [20, 0, 16, 0, 0]
C [12, 16, 0, 10, 0]
D [0, 0, 10, 0, 3]
E [0, 0, 0, 3, 0]
图的基本构成代码总结(包括深度优先搜索,广度优先搜索)
/**
* @author by CSDN@小智RE0
* @date 2021-11-25 16:33
* 图的创建以及基础使用
*/
public class Graphs
//定义存储顶点;
private List<String> nodeList;
//邻接矩阵;
private int[][] matrixArray;
//边的个数;
private int sideNum;
//是否被访问;
private boolean[] isVisit;
/**
* 初始化图
*
* @param n 顶点的数量
*/
public Graphs(int n)
this.nodeList = new ArrayList<>(n);
this.matrixArray = new int[n][n];
this.sideNum = 0;
this.isVisit = new boolean[5];
/**
* 广度优先搜索;
*/
public void toBFS()
for (int i = 0; i < getNodeNums(); i++)
if (!isVisit[i])
toBFS(isVisit, i);
System.out.println();
/**
* 广度优先搜索
*
* @param isVisit 当前的索引
* @param index 是否被访问的统计数组
*/
private void toBFS(boolean[] isVisit, int index)
//队列头结点的索引;
int headIndex;
//邻接顶点;
int adjacent;
//操作的队列;
LinkedList<Integer> queue = new LinkedList<>();
System.out.print(getNodeInfo(index) + "~~");
isVisit[index] = true;
queue.addLast(index);
//队列不为空就操作;
while (!queue.isEmpty())
//先把队头顶点出队;
headIndex = queue.removeFirst();
//找到这个出队顶点的邻接;
adjacent = getFirstAdjacency(headIndex);
while (adjacent != -1)
//若没有被访问,就操作;
if (!isVisit[adjacent])
System.out.print(getNodeInfo(adjacent) + "~~");
//将这个标记为已访问;
isVisit[adjacent] = true;
queue.addLast(adjacent);
//否则继续就跳过,继续在这个顶点这层继续查找;
adjacent = getNextAdjacency(headIndex, adjacent);
/**
* 深度优先搜索
*/
public void toDFS()
for (int i = 0; i < nodeList.size(); i++)
//若没访问过,就就进入;
if (!isVisit[i])
toDFS(isVisit, i);
System.out.println();
/**
* 深度优先搜索
*
* @param index 当前的索引;
* @param isVisit 是否被访问的统计数组
*/
private void toDFS(boolean[] isVisit, int index)
//输出当前的顶点;
System.out.print(getNodeInfo(index) + "->");
//当前顶点设置为已访问;
isVisit[index] = true;
//先查找这个顶点的首要邻接顶点;
int firstAdjacency = getFirstAdjacency(index);
//若存在就进行访问;
while (firstAdjacency != -1)
//是否被访问;
if (!isVisit[index])
toDFS(isVisit, firstAdjacency);
//若这个顶点已经被访问,则去找下一个邻接顶点;
firstAdjacency = getNextAdjacency(index, firstAdjacency);
/**
* 获取当前节点的下一个邻接节点的索引
*
* @param index 根据当前索引
*/
public int getFirstAdjacency(int index)
for (int i = 0; i < nodeList.size(); i++)
if (matrixArray[index][i] > 0)
return i;
return -1;
/**
* 根据前一个邻接顶点获取下一个邻接顶点的邻接节点索引
*
* @param v1 前一个邻接顶点
* @param v2 下一个邻接顶点
*/
public int getNextAdjacency(int v1, int v2)
for (int i = v2 + 1; i < nodeList.size(); i++)
if (matrixArray[v1][i] > 0)
return i;
return -1;
/**
* 添加新的顶点到集合中;
*
* @param node 添加的新顶点;
*/
public void addNode(String node)
this.nodeList.add(node);
/**
* 向邻接矩阵填入顶点之间的边 的权值
*
* @param v1 第一个顶点 (由0开始)
* @param v2 第二个顶点
* @param weight 边的权值
*/
public void addToArray(int v1, int v2, int weight)
//由于是无向图,所以两个方向都要标注;
this.matrixArray[v1][v2] = weight;
this.matrixArray[v2][v1] = weight;
//边的数量增加;
this.sideNum++;
/**
* 获取图中顶点的数量;
*
* @return 顶点数量
*/
public int getNodeNums()
return this.nodeList.size();
/**
* 获取图中边的数量;
*
* @return 边的数量
*/
public int getSideNum()
return this.sideNum;
/**
* 获取指定的顶点
*
* @param index 该节点在集合中的索引
* @return 指定顶点
*/
public String getNodeInfo(int index)
return this.nodeList.get(index);
/**
* 用邻接矩阵表示这张图
*/
public void describeGraphs()
for (int[] arr : matrixArray)
System.out.println(Arrays.toString(arr));
以上是关于学习数据结构笔记(14) --- [图]的主要内容，如果未能解决你的问题，请参考以下文章
unity shader学习笔记 shader基础结构以及Properties面板
[原创]java WEB学习笔记61：Struts2学习之路--通用标签 property，uri，param,set,push,if-else,itertor,sort,date,a标签等(代码片段